24.3.4相似三角形的应用(3)学案
文档属性
| 名称 | 24.3.4相似三角形的应用(3)学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-16 00:00:00 | ||
图片预览

文档简介
课 题:相似三角形的应用(3)
证明比例式、等积式
序 号:( 13)
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本63页例8
学习目标:利用相似三角形的性质证明比例式或等积式
重 点:利用相似三角形的性质证明比例式或等积式
难 点:构建相似三角形或转换等量关系
学法指导:合作探究
学 习 过 程
自主预习课本63页例8,完成下列各题:
1。如图,在△ABC中,高BD、CE交于点O,下列结论错误的是( )
A、CO·CE=CD·CA B、OE·OC=OD·OB
C、AD·AC=AE·AB D、CO·DO=BO·EO
什么情况下能得到比例式
(一)四条线段能直接构成两个相似三角形
问题1:如图,在平行四边形ABCD中, E是AD上的一点。求证:AE·OB=OE·CB
小结:证明等积式,通常通过证明三角形相似,对应边成比例得到。所以证明等积式,关键要找证明哪两个三角形相似,找三角形相似的方法是:先在等式左边选一条线段,看能否与等式右边的一条线段组成一个三角形,如能,那么剩下的两条线段组成另外一个三角形,然后想法证明这两个三角形相似。
跟踪练习:如图,已知,说明:·
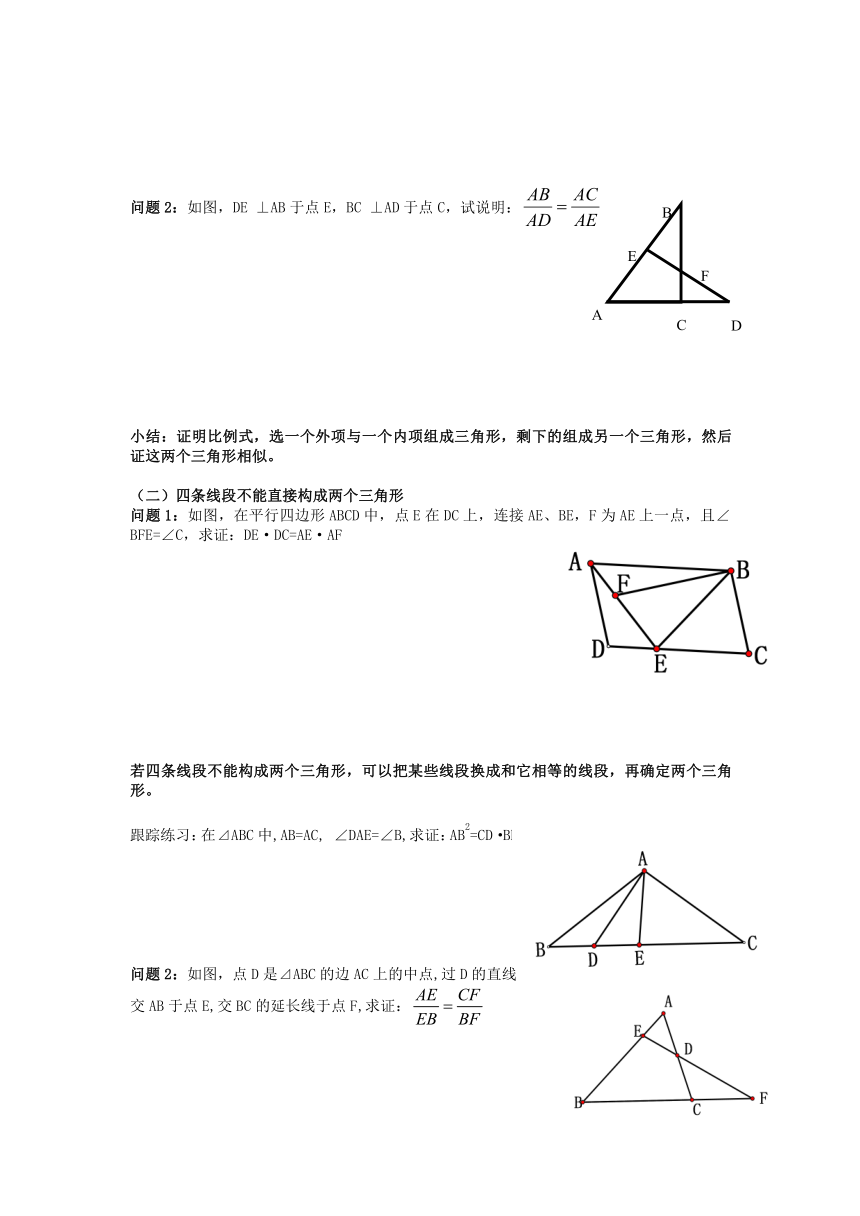
问题2:如图,DE ⊥AB于点E,BC ⊥AD于点C,试说明:
小结:证明比例式,选一个外项与一个内项组成三角形,剩下的组成另一个三角形,然后证这两个三角形相似。
(二)四条线段不能直接构成两个三角形
问题1:如图,在平行四边形ABCD中,点E在DC上,连接AE、BE,F为AE上一点,且∠BFE=∠C,求证:DE·DC=AE·AF
若四条线段不能构成两个三角形,可以把某些线段换成和它相等的线段,再确定两个三角形。
跟踪练习:在⊿ABC中,AB=AC, ∠DAE=∠B,求证:AB2=CD·BE
问题2:如图,点D是⊿ABC的边AC上的中点,过D的直线交AB于点E,交BC的延长线于点F,求证:
若四条线段不能构成两个三角形,也找不到相等的线段来替换,我们可以通过添加辅助线来构造相似三角形。
跟踪练习:如图,⊿ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB交BP延长线于F,求证:BP2=PE·PF
问题3:已知,如图,F为 ABCD边DC延长线上一点,连结AF,交BC于G,交BD于E,试说明AE2=EG·EF
小结:四条线段若不能凑成两个三角形,可以把其中两条线段比换成和它相等的线段的比。
1.如图,D、E是△ABC的边AB、AC上的点,且∠ADE=∠C.求证: AD·AB=AE·AC.
2.如图,在Rt△ABC中,∠BAC=90°,AB=AC,D为
BC的中点,E为AC上一点,点G在BE上,连结DG并延长
交AE于F,若∠FGE=45°求证:BD·BC=BG·BE
3. D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于F、G,且∠CAE=∠DBC,求证:BF2=FG·EF
4.如图,M是平行四边形ABCD的对角线BD上的一点,射线AM交BC于F,交DC的延长线于点H。
求证:AM2 =MF·MH
5.课外阅读:课本65---66页《 线段的平分》和《相似三角形与全等三角形》。
预 习 检 测
A
E
B
C
D
O
课 前 准 备
交 流 合 作
A
D
C
B
E
F
A
B
C
F
G
E
D
达 标 检 测
D
B
A
E
F
C
G
课 后 反 思
证明比例式、等积式
序 号:( 13)
年 级: 九年级 单元名称:第24章相似图形的性质
课 型: 新授课 上课时间:
学习内容:华东师大版课本63页例8
学习目标:利用相似三角形的性质证明比例式或等积式
重 点:利用相似三角形的性质证明比例式或等积式
难 点:构建相似三角形或转换等量关系
学法指导:合作探究
学 习 过 程
自主预习课本63页例8,完成下列各题:
1。如图,在△ABC中,高BD、CE交于点O,下列结论错误的是( )
A、CO·CE=CD·CA B、OE·OC=OD·OB
C、AD·AC=AE·AB D、CO·DO=BO·EO
什么情况下能得到比例式
(一)四条线段能直接构成两个相似三角形
问题1:如图,在平行四边形ABCD中, E是AD上的一点。求证:AE·OB=OE·CB
小结:证明等积式,通常通过证明三角形相似,对应边成比例得到。所以证明等积式,关键要找证明哪两个三角形相似,找三角形相似的方法是:先在等式左边选一条线段,看能否与等式右边的一条线段组成一个三角形,如能,那么剩下的两条线段组成另外一个三角形,然后想法证明这两个三角形相似。
跟踪练习:如图,已知,说明:·
问题2:如图,DE ⊥AB于点E,BC ⊥AD于点C,试说明:
小结:证明比例式,选一个外项与一个内项组成三角形,剩下的组成另一个三角形,然后证这两个三角形相似。
(二)四条线段不能直接构成两个三角形
问题1:如图,在平行四边形ABCD中,点E在DC上,连接AE、BE,F为AE上一点,且∠BFE=∠C,求证:DE·DC=AE·AF
若四条线段不能构成两个三角形,可以把某些线段换成和它相等的线段,再确定两个三角形。
跟踪练习:在⊿ABC中,AB=AC, ∠DAE=∠B,求证:AB2=CD·BE
问题2:如图,点D是⊿ABC的边AC上的中点,过D的直线交AB于点E,交BC的延长线于点F,求证:
若四条线段不能构成两个三角形,也找不到相等的线段来替换,我们可以通过添加辅助线来构造相似三角形。
跟踪练习:如图,⊿ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB交BP延长线于F,求证:BP2=PE·PF
问题3:已知,如图,F为 ABCD边DC延长线上一点,连结AF,交BC于G,交BD于E,试说明AE2=EG·EF
小结:四条线段若不能凑成两个三角形,可以把其中两条线段比换成和它相等的线段的比。
1.如图,D、E是△ABC的边AB、AC上的点,且∠ADE=∠C.求证: AD·AB=AE·AC.
2.如图,在Rt△ABC中,∠BAC=90°,AB=AC,D为
BC的中点,E为AC上一点,点G在BE上,连结DG并延长
交AE于F,若∠FGE=45°求证:BD·BC=BG·BE
3. D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于F、G,且∠CAE=∠DBC,求证:BF2=FG·EF
4.如图,M是平行四边形ABCD的对角线BD上的一点,射线AM交BC于F,交DC的延长线于点H。
求证:AM2 =MF·MH
5.课外阅读:课本65---66页《 线段的平分》和《相似三角形与全等三角形》。
预 习 检 测
A
E
B
C
D
O
课 前 准 备
交 流 合 作
A
D
C
B
E
F
A
B
C
F
G
E
D
达 标 检 测
D
B
A
E
F
C
G
课 后 反 思
