2022—2023学年沪教版(上海)数学七年级第一学期9.13提取公因式法(2) 课件(共9张PPT)
文档属性
| 名称 | 2022—2023学年沪教版(上海)数学七年级第一学期9.13提取公因式法(2) 课件(共9张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 416.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 12:46:41 | ||
图片预览



文档简介
(共9张PPT)
9.13 提取公因式(2)
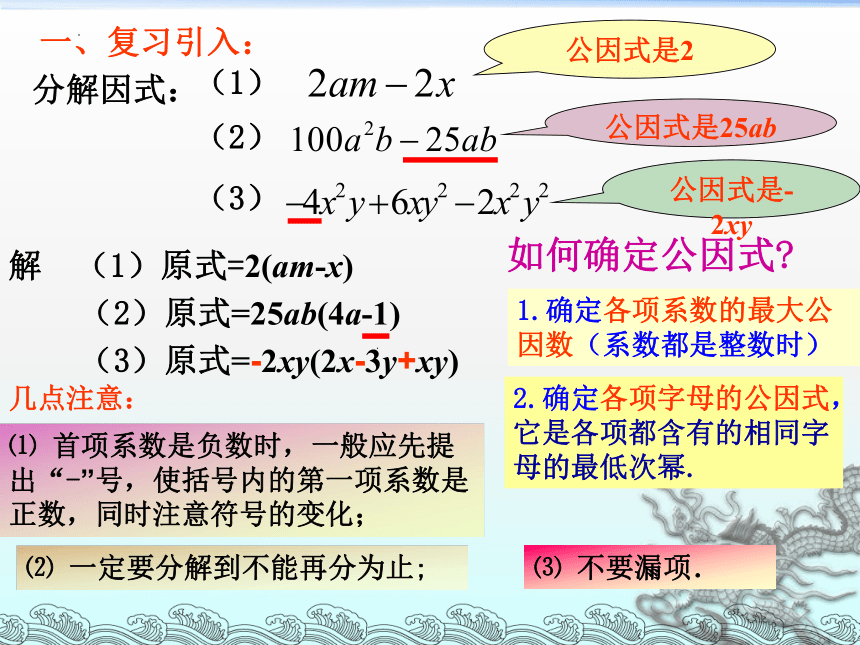
一、复习引入:
分解因式:
(1)
(2)
(3)
.
解 (1)原式=2(am-x)
(2)原式=25ab(4a-1)
(3)原式=-2xy(2x-3y+xy)
公因式是2
公因式是25ab
公因式是-2xy
如何确定公因式
1.确定各项系数的最大公因数(系数都是整数时)
2.确定各项字母的公因式,它是各项都含有的相同字母的最低次幂.
⑴ 首项系数是负数时,一般应先提出“-”号,使括号内的第一项系数是正数,同时注意符号的变化;
⑵ 一定要分解到不能再分为止;
⑶ 不要漏项.
几点注意:
思考:如何把
分解因式?
二.新授部分:
解 原式
把(x + y)看作一个整体,作为公因式
例题3 分解因式:
公因式是
解 原式
[
]
添加中括号
结果一般以小括号形式呈现
[
]
例题4(1)分解因式:
解 原式
公因式
添加中括号
解 原式
添加中括号
公因式
方法一
方法二
+
例题4(2)分解因式:
解 原式
提取公因式为多项式时,有时利用:
a-b与b-a
互为相反数
_
+
注意符号
小结:
才能找到公因式.
反馈练习:
填空:
2m
(1)
2m
(2)
x - y
(3)
( )
x2 - y
(4)
( )
例5 分解因式
公因式是2(x+y)
解 原式
[
]
添上中括号
去括号法则
+
3
这是因式分解的结果吗?
小结:因式分解结果中的各个因式不能再分解,即分解到不能分解为止.
三、课堂练习:课本P43/2.
合并同类项
还能再分解吗?
当n为偶数时,(a-b)n=(b-a)n
当n为奇数时,(a-b)n=-(b-a)n
四、课堂小结:
(一)提公因式法分解因式的一般步骤:
(1)找公因式;(2)提公因式;(3)分解到底.
(二)几点注意:
(1)关注符号,首项是“-”,一般提到括号外;
(2)利用 找公因式.
(3)不要漏项;
(4)分解到不能分解为止.
例如:(-2x+y)(3x-y),应写成-(2x-y)(3x-y)
例如:2m(a-b)-3n(b-a)=2m(a-b)+3n(a-b)
例如:5xy+x=x(5y+1),不要漏写1.
(5)因式分解的结果一般以小括号形式呈现.
五、布置作业 练习册:练习册第28页 7 .
9.13 提取公因式(2)
一、复习引入:
分解因式:
(1)
(2)
(3)
.
解 (1)原式=2(am-x)
(2)原式=25ab(4a-1)
(3)原式=-2xy(2x-3y+xy)
公因式是2
公因式是25ab
公因式是-2xy
如何确定公因式
1.确定各项系数的最大公因数(系数都是整数时)
2.确定各项字母的公因式,它是各项都含有的相同字母的最低次幂.
⑴ 首项系数是负数时,一般应先提出“-”号,使括号内的第一项系数是正数,同时注意符号的变化;
⑵ 一定要分解到不能再分为止;
⑶ 不要漏项.
几点注意:
思考:如何把
分解因式?
二.新授部分:
解 原式
把(x + y)看作一个整体,作为公因式
例题3 分解因式:
公因式是
解 原式
[
]
添加中括号
结果一般以小括号形式呈现
[
]
例题4(1)分解因式:
解 原式
公因式
添加中括号
解 原式
添加中括号
公因式
方法一
方法二
+
例题4(2)分解因式:
解 原式
提取公因式为多项式时,有时利用:
a-b与b-a
互为相反数
_
+
注意符号
小结:
才能找到公因式.
反馈练习:
填空:
2m
(1)
2m
(2)
x - y
(3)
( )
x2 - y
(4)
( )
例5 分解因式
公因式是2(x+y)
解 原式
[
]
添上中括号
去括号法则
+
3
这是因式分解的结果吗?
小结:因式分解结果中的各个因式不能再分解,即分解到不能分解为止.
三、课堂练习:课本P43/2.
合并同类项
还能再分解吗?
当n为偶数时,(a-b)n=(b-a)n
当n为奇数时,(a-b)n=-(b-a)n
四、课堂小结:
(一)提公因式法分解因式的一般步骤:
(1)找公因式;(2)提公因式;(3)分解到底.
(二)几点注意:
(1)关注符号,首项是“-”,一般提到括号外;
(2)利用 找公因式.
(3)不要漏项;
(4)分解到不能分解为止.
例如:(-2x+y)(3x-y),应写成-(2x-y)(3x-y)
例如:2m(a-b)-3n(b-a)=2m(a-b)+3n(a-b)
例如:5xy+x=x(5y+1),不要漏写1.
(5)因式分解的结果一般以小括号形式呈现.
五、布置作业 练习册:练习册第28页 7 .
