北师大版数学八年级上册 4.1函数课时练习(含答案)
文档属性
| 名称 | 北师大版数学八年级上册 4.1函数课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 128.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 19:14:57 | ||
图片预览

文档简介
2022-2023年北师大版数学八年级上册4.1
《函数》课时练习
一 、选择题
1.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
2.在圆的周长C=2πr中,常量与变量分别是( )
A.2是常量,C、π、r是变量
B.2是常量,C、r是变量
C.C、2是常量,r是变量
D.D.2是常量,C、r是变量
3.下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A.(1) B.(2) C.(3) D.(4)
4.在下列各图象中,y不是x函数的是( )
A. B. C. D.
5.甲、乙两地相距320 km,一货车从甲地出发以80 km/h的速度匀速向乙地行驶,则货车距离乙地的路程s(km)与时间t(h)之间的函数表达式是( )
A.s=320t B.s=80t C.s=320-80t D.s=320-4t
6.长方形周长为30,设长为x,宽为y,则y与x的函数关系式为( )
A.y=30﹣x B.y=30﹣2x C.y=15﹣x D.y=15+2x
7.在函数中,自变量x的取值范围是( )
A.x< B.x≠﹣ C.x≠ D.x>
8.在函数y=﹣中,自变量x的取值范围是( )
A.x>﹣1 B.x≥﹣1 C.x>﹣1且x≠2 D.x≥﹣1且x≠2
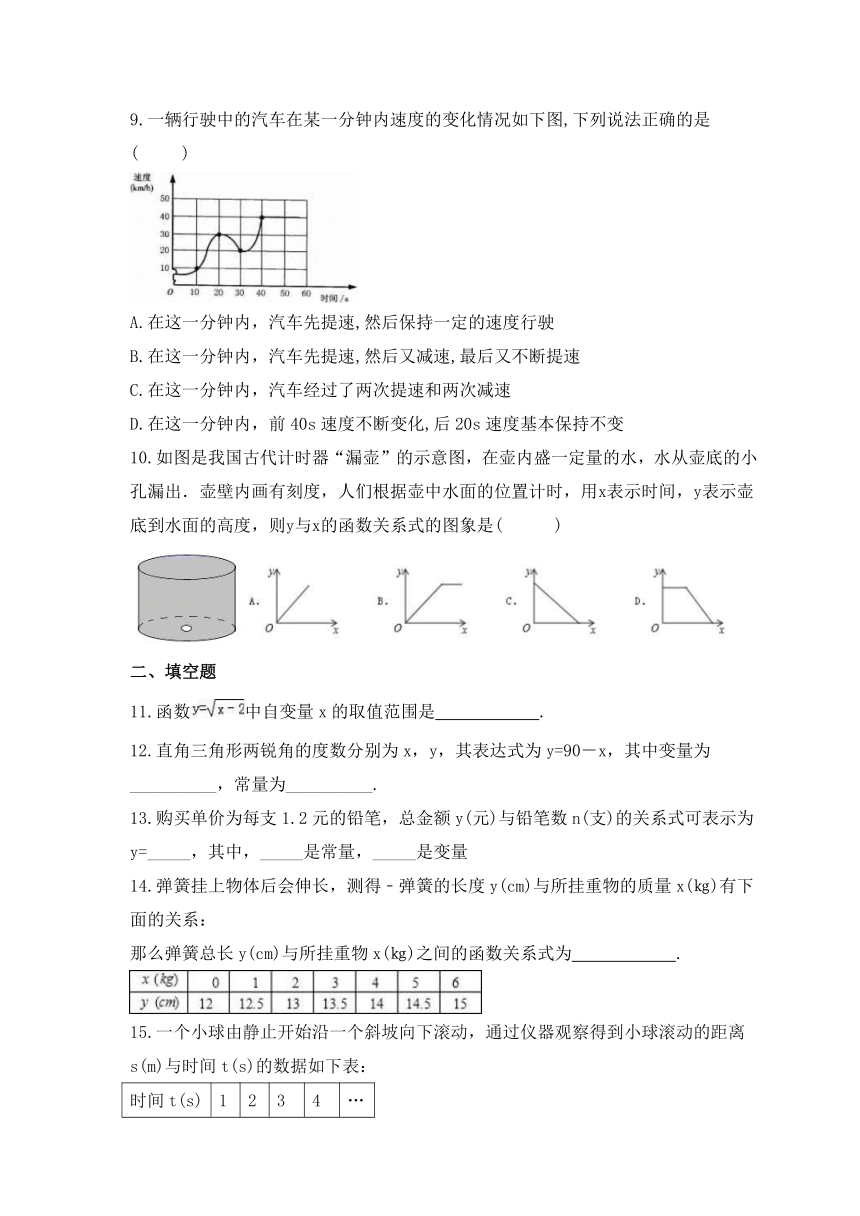
9.一辆行驶中的汽车在某一分钟内速度的变化情况如下图,下列说法正确的是( )
A.在这一分钟内,汽车先提速,然后保持一定的速度行驶
B.在这一分钟内,汽车先提速,然后又减速,最后又不断提速
C.在这一分钟内,汽车经过了两次提速和两次减速
D.在这一分钟内,前40s速度不断变化,后20s速度基本保持不变
10.如图是我国古代计时器“漏壶”的示意图,在壶内盛一定量的水,水从壶底的小孔漏出.壶壁内画有刻度,人们根据壶中水面的位置计时,用x表示时间,y表示壶底到水面的高度,则y与x的函数关系式的图象是( )
二 、填空题
11.函数中自变量x的取值范围是 .
12.直角三角形两锐角的度数分别为x,y,其表达式为y=90-x,其中变量为__________,常量为__________.
13.购买单价为每支1.2元的铅笔,总金额y(元)与铅笔数n(支)的关系式可表示为y=_____,其中,_____是常量,_____是变量
14.弹簧挂上物体后会伸长,测得﹣弹簧的长度y(cm)与所挂重物的质量x(㎏)有下面的关系:
那么弹簧总长y(cm)与所挂重物x(㎏)之间的函数关系式为 .
15.一个小球由静止开始沿一个斜坡向下滚动,通过仪器观察得到小球滚动的距离s(m)与时间t(s)的数据如下表:
时间t(s) 1 2 3 4 …
距离s(m) 2 8 18 32 …
写出用t表示s的关系式:________.
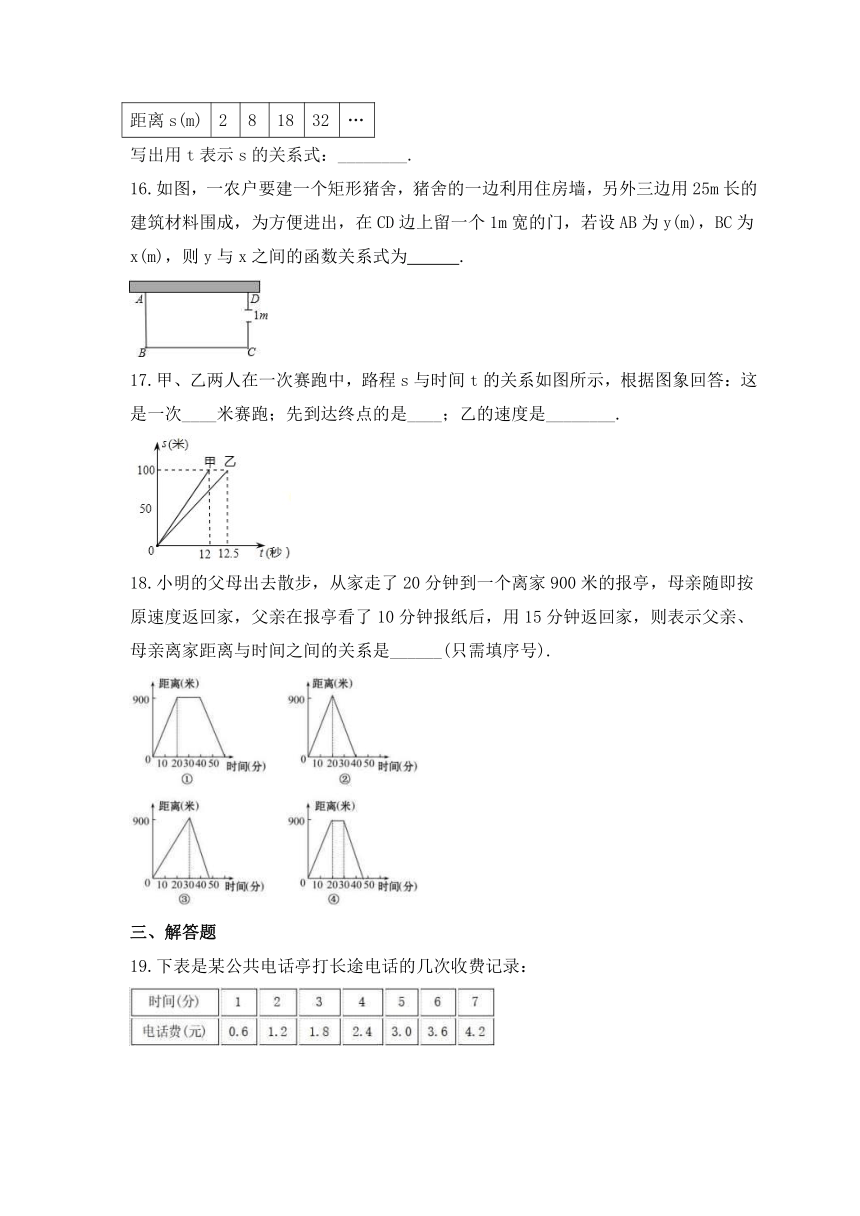
16.如图,一农户要建一个矩形猪舍,猪舍的一边利用住房墙,另外三边用25m长的建筑材料围成,为方便进出,在CD边上留一个1m宽的门,若设AB为y(m),BC为x(m),则y与x之间的函数关系式为 .
17.甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,根据图象回答:这是一次____米赛跑;先到达终点的是____;乙的速度是________.
18.小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是______(只需填序号).
三 、解答题
19.下表是某公共电话亭打长途电话的几次收费记录:
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
20.已知矩形周长为18,其中一条边长为x,设另一边长为y.
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围.
21.在国内投寄平信应付邮资如下表:
信件质量x(克) 0<x≤20 0<x≤40 0<x≤60
邮资y(元) 0.80 1.60 2.40
①y是x的函数吗?为什么?
②分别求当x=5,10,30,50时的函数值.
22.某剧院的观众席的座位为扇形,且按下列方式设置:
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间函数的表达式.
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
23.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系(其中0≤x≤30).
提出概念所用时间(x) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表中反映了哪两个变量之间的关系?那个是自变量?哪个是因变量?
(2)根据表格中的数据,你认为提出概念所用时间为几分钟时,学生的接受能力最强?
(3)从表格中可知,当提出概念所用时间x在什么范围内,学生的接受能力逐步增强?当提出概念所用时间x在什么范围内,学生的接受能力逐步降低?
(4)根据表格大致估计当提出概念所用时间为23分钟时,学生对概念的接受能力是多少.
参考答案
1.C
2.B.
3.D
4.C
5.C.
6.C
7.C
8.D.
9.D
10.C
11.答案为:x≥2.
12.答案为:x,y,-1,90
13.答案为:y=1.2n(n为自然数);1.2;n、y.
14.答案为:y=0.5x+12.
15.答案为:s=2t2(t≥0)
16.答案为:y=13﹣x.
17.答案为:100 甲 8米/秒
18.答案为:④②
19.解:(1)反映的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据表格中的数据得出:每增加1分钟,电话费增加0.6元;
(3)由表格中的数据直接得出:丽丽打了5分钟电话,电话费需付3元.
20.解:(1)∵矩形周长为18,其中一条边长为x,设另一边长为y,
∴2(x+y)=18,则y=9﹣x;
(2)由题意可得:9﹣x>0,解得:0<x<9.
21.解:(1)y是x的函数,当x取定一个值时,y都有唯一确定的值与其对应;
(2)当x=5时,y=0.80;
当x=10时,y=0.80;
当x=30时,y=1.60;
当x=50时,y=2.40.
22.解:(1)由图表中数据可得,当x每增加1时,y增加3.
(2)由题意,得y=50+3(x-1)=3x+47.
(3)某一排不可能有90个座位.理由如下:
令y=90,得3x+47=90,解得x=.
∵x为整数,
∴某一排不可能有90个座位.
23.解:(1)反映了提出概念所用的时间x和对概念接受能力y两个变量之间的关系;
其中x是自变量,y是因变量.
(2)提出概念所用的时间为13分钟时,学生的接受能力最强.
(3)当x在2分钟至13分钟的范围内,学生的接受能力逐步增强.
当x在13分钟至20分钟的范围内,学生的接受能力逐步降低.
(4)估计当提出概念所用的时间为23分钟时,学生的接受能力为49.9.
《函数》课时练习
一 、选择题
1.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
2.在圆的周长C=2πr中,常量与变量分别是( )
A.2是常量,C、π、r是变量
B.2是常量,C、r是变量
C.C、2是常量,r是变量
D.D.2是常量,C、r是变量
3.下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A.(1) B.(2) C.(3) D.(4)
4.在下列各图象中,y不是x函数的是( )
A. B. C. D.
5.甲、乙两地相距320 km,一货车从甲地出发以80 km/h的速度匀速向乙地行驶,则货车距离乙地的路程s(km)与时间t(h)之间的函数表达式是( )
A.s=320t B.s=80t C.s=320-80t D.s=320-4t
6.长方形周长为30,设长为x,宽为y,则y与x的函数关系式为( )
A.y=30﹣x B.y=30﹣2x C.y=15﹣x D.y=15+2x
7.在函数中,自变量x的取值范围是( )
A.x< B.x≠﹣ C.x≠ D.x>
8.在函数y=﹣中,自变量x的取值范围是( )
A.x>﹣1 B.x≥﹣1 C.x>﹣1且x≠2 D.x≥﹣1且x≠2
9.一辆行驶中的汽车在某一分钟内速度的变化情况如下图,下列说法正确的是( )
A.在这一分钟内,汽车先提速,然后保持一定的速度行驶
B.在这一分钟内,汽车先提速,然后又减速,最后又不断提速
C.在这一分钟内,汽车经过了两次提速和两次减速
D.在这一分钟内,前40s速度不断变化,后20s速度基本保持不变
10.如图是我国古代计时器“漏壶”的示意图,在壶内盛一定量的水,水从壶底的小孔漏出.壶壁内画有刻度,人们根据壶中水面的位置计时,用x表示时间,y表示壶底到水面的高度,则y与x的函数关系式的图象是( )
二 、填空题
11.函数中自变量x的取值范围是 .
12.直角三角形两锐角的度数分别为x,y,其表达式为y=90-x,其中变量为__________,常量为__________.
13.购买单价为每支1.2元的铅笔,总金额y(元)与铅笔数n(支)的关系式可表示为y=_____,其中,_____是常量,_____是变量
14.弹簧挂上物体后会伸长,测得﹣弹簧的长度y(cm)与所挂重物的质量x(㎏)有下面的关系:
那么弹簧总长y(cm)与所挂重物x(㎏)之间的函数关系式为 .
15.一个小球由静止开始沿一个斜坡向下滚动,通过仪器观察得到小球滚动的距离s(m)与时间t(s)的数据如下表:
时间t(s) 1 2 3 4 …
距离s(m) 2 8 18 32 …
写出用t表示s的关系式:________.
16.如图,一农户要建一个矩形猪舍,猪舍的一边利用住房墙,另外三边用25m长的建筑材料围成,为方便进出,在CD边上留一个1m宽的门,若设AB为y(m),BC为x(m),则y与x之间的函数关系式为 .
17.甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,根据图象回答:这是一次____米赛跑;先到达终点的是____;乙的速度是________.
18.小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是______(只需填序号).
三 、解答题
19.下表是某公共电话亭打长途电话的几次收费记录:
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
20.已知矩形周长为18,其中一条边长为x,设另一边长为y.
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围.
21.在国内投寄平信应付邮资如下表:
信件质量x(克) 0<x≤20 0<x≤40 0<x≤60
邮资y(元) 0.80 1.60 2.40
①y是x的函数吗?为什么?
②分别求当x=5,10,30,50时的函数值.
22.某剧院的观众席的座位为扇形,且按下列方式设置:
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间函数的表达式.
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
23.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系(其中0≤x≤30).
提出概念所用时间(x) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表中反映了哪两个变量之间的关系?那个是自变量?哪个是因变量?
(2)根据表格中的数据,你认为提出概念所用时间为几分钟时,学生的接受能力最强?
(3)从表格中可知,当提出概念所用时间x在什么范围内,学生的接受能力逐步增强?当提出概念所用时间x在什么范围内,学生的接受能力逐步降低?
(4)根据表格大致估计当提出概念所用时间为23分钟时,学生对概念的接受能力是多少.
参考答案
1.C
2.B.
3.D
4.C
5.C.
6.C
7.C
8.D.
9.D
10.C
11.答案为:x≥2.
12.答案为:x,y,-1,90
13.答案为:y=1.2n(n为自然数);1.2;n、y.
14.答案为:y=0.5x+12.
15.答案为:s=2t2(t≥0)
16.答案为:y=13﹣x.
17.答案为:100 甲 8米/秒
18.答案为:④②
19.解:(1)反映的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)根据表格中的数据得出:每增加1分钟,电话费增加0.6元;
(3)由表格中的数据直接得出:丽丽打了5分钟电话,电话费需付3元.
20.解:(1)∵矩形周长为18,其中一条边长为x,设另一边长为y,
∴2(x+y)=18,则y=9﹣x;
(2)由题意可得:9﹣x>0,解得:0<x<9.
21.解:(1)y是x的函数,当x取定一个值时,y都有唯一确定的值与其对应;
(2)当x=5时,y=0.80;
当x=10时,y=0.80;
当x=30时,y=1.60;
当x=50时,y=2.40.
22.解:(1)由图表中数据可得,当x每增加1时,y增加3.
(2)由题意,得y=50+3(x-1)=3x+47.
(3)某一排不可能有90个座位.理由如下:
令y=90,得3x+47=90,解得x=.
∵x为整数,
∴某一排不可能有90个座位.
23.解:(1)反映了提出概念所用的时间x和对概念接受能力y两个变量之间的关系;
其中x是自变量,y是因变量.
(2)提出概念所用的时间为13分钟时,学生的接受能力最强.
(3)当x在2分钟至13分钟的范围内,学生的接受能力逐步增强.
当x在13分钟至20分钟的范围内,学生的接受能力逐步降低.
(4)估计当提出概念所用的时间为23分钟时,学生的接受能力为49.9.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
