2013-2014学年度沪科版九年级上学期第一次月考数学试卷(附答案解析)
文档属性
| 名称 | 2013-2014学年度沪科版九年级上学期第一次月考数学试卷(附答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 97.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-23 00:00:00 | ||
图片预览




文档简介
2013-2014学年度沪科版九年级(上)第一次段考
数学试卷(附答案解析)
(温馨提示:本卷满分150分,答题时间120分钟)
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列函数不属于二次函数的是( )
A. y=(x﹣1)(x+2) B. y=(x+1)2 C. y=1﹣x2 D. y=2(x+3)2﹣2x2
2.(抛物线y=(x+2)2+1的顶点坐标是( )
A. (2,1) B. (﹣2,1) C. (2,﹣1) D. (﹣2,﹣1)
3.函数y=x2﹣4x+3图象顶点坐标是( )
A. (2,﹣1) B. (﹣2,1) C. (﹣2,﹣1) D. (2,1)
4.已知二次函数y=mx2+x+m(m﹣2)的图象经过原点,则m的值为( )
A. 0或2 B. 0 C. 2 D. 无法确定
5.二次函数y=x2+bx+c的图象上有两点(3,4)和(﹣5,4),则此拋物线的对称轴是直线( )
A. x=﹣1 B. x=1 C. x=2 D. x=3
6.函数y=2x2﹣3x+4经过的象限是( )
A. 一,二,三象限 B. 一,二象限 C. 三,四象限 D. 一,二,四象限
7.抛物线y=x2﹣bx+8的顶点在x轴上,则b的值一定为( )
A. 4? B. ﹣4? C. 2或﹣2? D. 4或﹣4
8.二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
A. a>0 B. b>0 C. c<0 D. abc>0
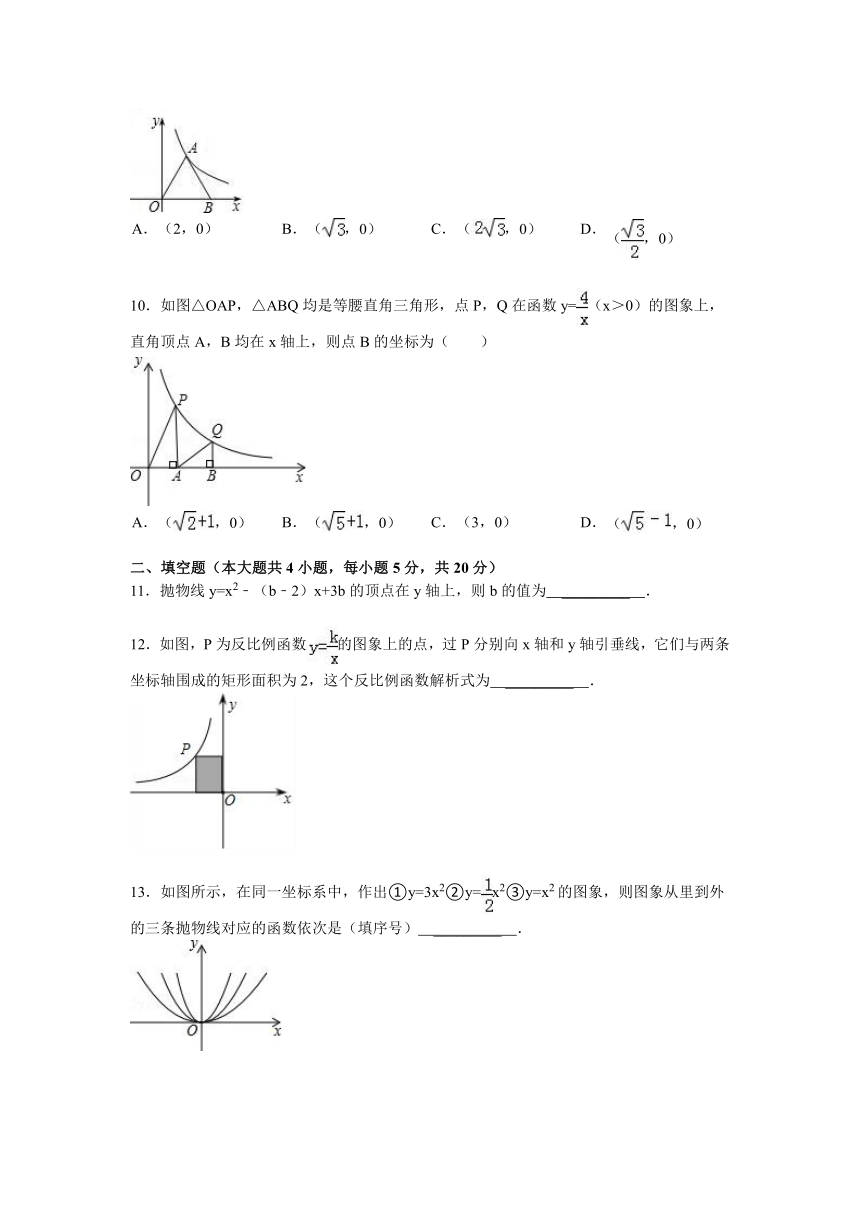
9.如图,正△AOB的顶点A在反比例函数y=(x>0)的图象上,则点B的坐标为( )
A. (2,0) B. (,0) C. (,0) D. (,0)
10.如图△OAP,△ABQ均是等腰直角三角形,点P,Q在函数y=(x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )
A. (,0) B. (,0) C. (3,0) D. (,0)
二、填空题(本大题共4小题,每小题5分,共20分)
11.抛物线y=x2﹣(b﹣2)x+3b的顶点在y轴上,则b的值为 _________ .
12.如图,P为反比例函数的图象上的点,过P分别向x轴和y轴引垂线,它们与两条坐标轴围成的矩形面积为2,这个反比例函数解析式为 _________ .
13.如图所示,在同一坐标系中,作出①y=3x2②y=x2③y=x2的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) _________ .
14.把抛物线y=ax2+bx+c先向右平移2个单位,再向下平移5个单位得到抛物线y=x2﹣2x﹣2,那么a= _________ ,b= _________ ,c= _________ .
三、(本题共2小题,每小题8分,满分16分)
15.拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为m时,水面的宽度为多少米?
16.已知二次函数的顶点坐标为(1,4),且其图象经过点(﹣2,﹣5),求此二次函数的解析式.
四、(本题共2小题,每小题8分,满分16分)
17.用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2.
(1)求出y与x的函数关系式.
(2)当边长x为多少时,矩形的面积最大,最大面积是多少?
18.如图,已知一抛物线形大门,其地面宽度AB=18m.一同学站在门内,在离门脚B点1m远的D处,垂直地面立起一根1.7m长的木杆,其顶端恰好顶在抛物线形门上C处.根据这些条件,请你求出该大门的高h.
五、(本题共2小题,每小题10分,满分20分)
19.已知y=y1+y2,y1与x成正比例,y2与x﹣2成反比例,且当x=1时,y=﹣1;当x=3时,y=5.求y与x的函数关系式.
20.抛物线y=﹣2x2+8x﹣6.
(1)用配方法求顶点坐标,对称轴;
(2)x取何值时,y随x的增大而减小?
(3)x取何值时,y=0;x取何值时,y>0;x取何值时,y<0.
六、(本大题满分12分)
21.已知抛物线y=ax2+6x﹣8与直线y=﹣3x相交于点A(1,m).
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到y=ax2的图象.
七、(本大题满分12分)
22.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,安装在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线的形状如图(1)和(2)所示,建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系式是y=﹣x2+2x+,请回答下列问题.
(1)柱子OA的高度为多少米?
(2)喷出的水流距水平面的最大高度是多少?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
八、(本大题满分14分)
23.如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
参考答案与试题解析
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A C A B D B A B
第8题解析:
由抛物线的开口方向向上可以得到a>0,由与y轴的交点为在y轴的负半轴上可以推出c<0,而对称轴为x=>0可以推出b<0,由此可以确定abc的符号.
解:∵抛物线的开口方向向上,∴a>0,∵与y轴的交点为在y轴的负半轴上,∴c<0,∵对称轴为x=>0,∴a、b异号,即b<0,∴abc>0.故选B.
第9题解析:
过点A作AC⊥y轴于C,根据已知条件知道△OAB是正三角形,然后设AC=a,则OC=a,这样点A则坐标可以用a表示,再把这点代入反比例函数的解析式就可以求出a从而求出点B的坐标.
解:如图,过点A作AC⊥y轴于C,∵△OAB是正三角形,∴∠AOB=60°,∴∠AOC=30°,∴设AC=a,则OC=a,∴点A则坐标是(a,a),把这点代入反比例函数的解析式就得到a=,∴a=±1,∵x>0,∴a=1,则OA=2,∴OB=2,则点B的坐标为(2,0).故选A.
二、填空题
11.2
12.
13.①③②
14.a=1,b=2,c=3
三、(本题共2小题,每小题8分,满分16分)
15. 解:在y=﹣中,当y=﹣时,x=±5,故水面的宽度为2×5=10米.答:水面的宽度为10米.
16. 解:设此二次函数的解析式为y=a(x﹣1)2+4(a≠0).∵其图象经过点(﹣2,﹣5),∴a(﹣2﹣1)2+4=﹣5,∴a=﹣1,∴y=﹣(x﹣1)2+4=﹣x2+2x+3.
四、(本题共2小题,每小题8分,满分16分)
17. 解:(1)已知一边长为xcm,则另一边长为(10﹣x).则y=x(10﹣x)化简可得y=﹣x2+10x(2)y=10x﹣x2=﹣(x2﹣10x)=﹣(x﹣5)2+25,所以当x=5时,矩形的面积最大,最大为25cm2.
18. 解:解法一:如图1,建立平面直角坐标系.设抛物线解析式为y=ax2+bx.由题意知B、C两点坐标分别为B(18,0),C(17,1.7),把B、C两点坐标代入抛物线解析式得解得∴抛物线的解析式为y=﹣0.1x2+1.8x=﹣0.1(x2﹣18x+81﹣81)=﹣0.1(x﹣9)2+8.1.∴该大门的高h为8.1m.解法二:如图2,建立平面直角坐标系.设抛物线解析式为y=ax2.由题意得B、C两点坐标分别为B(9,﹣h),C(8,﹣h+1.7).把B、C两点坐标代入y=ax2得解得∴y=﹣0.1x2.∴该大门的高h为8.1m.说明:此题还可以以AB所在直线为x轴,AB中点为原点,建立直角坐标系,可得抛物线解析式为y=﹣0.1x2+8.1.
五、(本题共2小题,每小题10分,满分20分)
19. 解:设y1=k1x(k1≠0),y2=∴y=k1x+∵当x=1时,y=﹣1;当x=3时,y=5,∴.所以.所以y=x+.
20. 解:(1)∵y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2,∴顶点坐标为(2,2),对称轴为直线x=2;(2)∵a=﹣2<0,抛物线开口向下,对称轴为直线x=2,∴当x>2时,y随x的增大而减小;(3)令y=0,即﹣2x2+8x﹣6=0,解得x=1或3,抛物线开口向下,∴当x=1或x=3时,y=0;当1<x<3时,y>0;当x<1或x>3时,y<0.
六、(本大题满分12分)
21. 解:(1)∵点A(1,m)在直线y=﹣3x上,∴m=﹣3×1=﹣3.把x=1,y=﹣3代入y=ax2+6x﹣8,求得a=﹣1.∴抛物线的解析式是y=﹣x2+6x﹣8.(2)y=﹣x2+6x﹣8=﹣(x﹣3)2+1.∴顶点坐标为(3,1).∴把抛物线y=﹣x2+6x﹣8向左平移3个单位长度得到y=﹣x2+1的图象,再把y=﹣x2+1的图象向下平移1个单位长度(或向左平移3个单位再向下平移1个单位)得到y=﹣x2的图象.
七、(本大题满分12分)
22. 解:(1)当x=0时,y=,故OA的高度为1.25米;(2)∵y=﹣x2+2x+=﹣(x﹣1)2+2.25,∴顶点是(1,2.25),故喷出的水流距水面的最大高度是2.25米;(3)解方程﹣x2+2x+=0,得x1=﹣,x2=,∴B点坐标为,∴OB=.故不计其他因素,水池的半径至少要2.5米,才能使喷出的水流不至于落在水池外.
八、(本大题满分14分)
23. 解:(1)∵当球运行的水平距离为2.5米时,达到最大高度3.5米,∴抛物线的顶点坐标为(0,3.5),∴设抛物线的表达式为y=ax2+3.5.由图知图象过以下点:(1.5,3.05).∴2.25a+3.5=3.05,解得:a=﹣0.2,∴抛物线的表达式为y=﹣0.2x2+3.5.(2)设球出手时,他跳离地面的高度为hm,因为(1)中求得y=﹣0.2x2+3.5,则球出手时,球的高度为h+1.8+0.25=(h+2.05)m,∴h+2.05=﹣0.2×(﹣2.5)2+3.5,∴h=0.2(m).答:球出手时,他跳离地面的高度为0.2m.
数学试卷(附答案解析)
(温馨提示:本卷满分150分,答题时间120分钟)
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列函数不属于二次函数的是( )
A. y=(x﹣1)(x+2) B. y=(x+1)2 C. y=1﹣x2 D. y=2(x+3)2﹣2x2
2.(抛物线y=(x+2)2+1的顶点坐标是( )
A. (2,1) B. (﹣2,1) C. (2,﹣1) D. (﹣2,﹣1)
3.函数y=x2﹣4x+3图象顶点坐标是( )
A. (2,﹣1) B. (﹣2,1) C. (﹣2,﹣1) D. (2,1)
4.已知二次函数y=mx2+x+m(m﹣2)的图象经过原点,则m的值为( )
A. 0或2 B. 0 C. 2 D. 无法确定
5.二次函数y=x2+bx+c的图象上有两点(3,4)和(﹣5,4),则此拋物线的对称轴是直线( )
A. x=﹣1 B. x=1 C. x=2 D. x=3
6.函数y=2x2﹣3x+4经过的象限是( )
A. 一,二,三象限 B. 一,二象限 C. 三,四象限 D. 一,二,四象限
7.抛物线y=x2﹣bx+8的顶点在x轴上,则b的值一定为( )
A. 4? B. ﹣4? C. 2或﹣2? D. 4或﹣4
8.二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
A. a>0 B. b>0 C. c<0 D. abc>0
9.如图,正△AOB的顶点A在反比例函数y=(x>0)的图象上,则点B的坐标为( )
A. (2,0) B. (,0) C. (,0) D. (,0)
10.如图△OAP,△ABQ均是等腰直角三角形,点P,Q在函数y=(x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )
A. (,0) B. (,0) C. (3,0) D. (,0)
二、填空题(本大题共4小题,每小题5分,共20分)
11.抛物线y=x2﹣(b﹣2)x+3b的顶点在y轴上,则b的值为 _________ .
12.如图,P为反比例函数的图象上的点,过P分别向x轴和y轴引垂线,它们与两条坐标轴围成的矩形面积为2,这个反比例函数解析式为 _________ .
13.如图所示,在同一坐标系中,作出①y=3x2②y=x2③y=x2的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) _________ .
14.把抛物线y=ax2+bx+c先向右平移2个单位,再向下平移5个单位得到抛物线y=x2﹣2x﹣2,那么a= _________ ,b= _________ ,c= _________ .
三、(本题共2小题,每小题8分,满分16分)
15.拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为m时,水面的宽度为多少米?
16.已知二次函数的顶点坐标为(1,4),且其图象经过点(﹣2,﹣5),求此二次函数的解析式.
四、(本题共2小题,每小题8分,满分16分)
17.用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2.
(1)求出y与x的函数关系式.
(2)当边长x为多少时,矩形的面积最大,最大面积是多少?
18.如图,已知一抛物线形大门,其地面宽度AB=18m.一同学站在门内,在离门脚B点1m远的D处,垂直地面立起一根1.7m长的木杆,其顶端恰好顶在抛物线形门上C处.根据这些条件,请你求出该大门的高h.
五、(本题共2小题,每小题10分,满分20分)
19.已知y=y1+y2,y1与x成正比例,y2与x﹣2成反比例,且当x=1时,y=﹣1;当x=3时,y=5.求y与x的函数关系式.
20.抛物线y=﹣2x2+8x﹣6.
(1)用配方法求顶点坐标,对称轴;
(2)x取何值时,y随x的增大而减小?
(3)x取何值时,y=0;x取何值时,y>0;x取何值时,y<0.
六、(本大题满分12分)
21.已知抛物线y=ax2+6x﹣8与直线y=﹣3x相交于点A(1,m).
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到y=ax2的图象.
七、(本大题满分12分)
22.某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,安装在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线的形状如图(1)和(2)所示,建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系式是y=﹣x2+2x+,请回答下列问题.
(1)柱子OA的高度为多少米?
(2)喷出的水流距水平面的最大高度是多少?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
八、(本大题满分14分)
23.如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
参考答案与试题解析
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A C A B D B A B
第8题解析:
由抛物线的开口方向向上可以得到a>0,由与y轴的交点为在y轴的负半轴上可以推出c<0,而对称轴为x=>0可以推出b<0,由此可以确定abc的符号.
解:∵抛物线的开口方向向上,∴a>0,∵与y轴的交点为在y轴的负半轴上,∴c<0,∵对称轴为x=>0,∴a、b异号,即b<0,∴abc>0.故选B.
第9题解析:
过点A作AC⊥y轴于C,根据已知条件知道△OAB是正三角形,然后设AC=a,则OC=a,这样点A则坐标可以用a表示,再把这点代入反比例函数的解析式就可以求出a从而求出点B的坐标.
解:如图,过点A作AC⊥y轴于C,∵△OAB是正三角形,∴∠AOB=60°,∴∠AOC=30°,∴设AC=a,则OC=a,∴点A则坐标是(a,a),把这点代入反比例函数的解析式就得到a=,∴a=±1,∵x>0,∴a=1,则OA=2,∴OB=2,则点B的坐标为(2,0).故选A.
二、填空题
11.2
12.
13.①③②
14.a=1,b=2,c=3
三、(本题共2小题,每小题8分,满分16分)
15. 解:在y=﹣中,当y=﹣时,x=±5,故水面的宽度为2×5=10米.答:水面的宽度为10米.
16. 解:设此二次函数的解析式为y=a(x﹣1)2+4(a≠0).∵其图象经过点(﹣2,﹣5),∴a(﹣2﹣1)2+4=﹣5,∴a=﹣1,∴y=﹣(x﹣1)2+4=﹣x2+2x+3.
四、(本题共2小题,每小题8分,满分16分)
17. 解:(1)已知一边长为xcm,则另一边长为(10﹣x).则y=x(10﹣x)化简可得y=﹣x2+10x(2)y=10x﹣x2=﹣(x2﹣10x)=﹣(x﹣5)2+25,所以当x=5时,矩形的面积最大,最大为25cm2.
18. 解:解法一:如图1,建立平面直角坐标系.设抛物线解析式为y=ax2+bx.由题意知B、C两点坐标分别为B(18,0),C(17,1.7),把B、C两点坐标代入抛物线解析式得解得∴抛物线的解析式为y=﹣0.1x2+1.8x=﹣0.1(x2﹣18x+81﹣81)=﹣0.1(x﹣9)2+8.1.∴该大门的高h为8.1m.解法二:如图2,建立平面直角坐标系.设抛物线解析式为y=ax2.由题意得B、C两点坐标分别为B(9,﹣h),C(8,﹣h+1.7).把B、C两点坐标代入y=ax2得解得∴y=﹣0.1x2.∴该大门的高h为8.1m.说明:此题还可以以AB所在直线为x轴,AB中点为原点,建立直角坐标系,可得抛物线解析式为y=﹣0.1x2+8.1.
五、(本题共2小题,每小题10分,满分20分)
19. 解:设y1=k1x(k1≠0),y2=∴y=k1x+∵当x=1时,y=﹣1;当x=3时,y=5,∴.所以.所以y=x+.
20. 解:(1)∵y=﹣2x2+8x﹣6=﹣2(x﹣2)2+2,∴顶点坐标为(2,2),对称轴为直线x=2;(2)∵a=﹣2<0,抛物线开口向下,对称轴为直线x=2,∴当x>2时,y随x的增大而减小;(3)令y=0,即﹣2x2+8x﹣6=0,解得x=1或3,抛物线开口向下,∴当x=1或x=3时,y=0;当1<x<3时,y>0;当x<1或x>3时,y<0.
六、(本大题满分12分)
21. 解:(1)∵点A(1,m)在直线y=﹣3x上,∴m=﹣3×1=﹣3.把x=1,y=﹣3代入y=ax2+6x﹣8,求得a=﹣1.∴抛物线的解析式是y=﹣x2+6x﹣8.(2)y=﹣x2+6x﹣8=﹣(x﹣3)2+1.∴顶点坐标为(3,1).∴把抛物线y=﹣x2+6x﹣8向左平移3个单位长度得到y=﹣x2+1的图象,再把y=﹣x2+1的图象向下平移1个单位长度(或向左平移3个单位再向下平移1个单位)得到y=﹣x2的图象.
七、(本大题满分12分)
22. 解:(1)当x=0时,y=,故OA的高度为1.25米;(2)∵y=﹣x2+2x+=﹣(x﹣1)2+2.25,∴顶点是(1,2.25),故喷出的水流距水面的最大高度是2.25米;(3)解方程﹣x2+2x+=0,得x1=﹣,x2=,∴B点坐标为,∴OB=.故不计其他因素,水池的半径至少要2.5米,才能使喷出的水流不至于落在水池外.
八、(本大题满分14分)
23. 解:(1)∵当球运行的水平距离为2.5米时,达到最大高度3.5米,∴抛物线的顶点坐标为(0,3.5),∴设抛物线的表达式为y=ax2+3.5.由图知图象过以下点:(1.5,3.05).∴2.25a+3.5=3.05,解得:a=﹣0.2,∴抛物线的表达式为y=﹣0.2x2+3.5.(2)设球出手时,他跳离地面的高度为hm,因为(1)中求得y=﹣0.2x2+3.5,则球出手时,球的高度为h+1.8+0.25=(h+2.05)m,∴h+2.05=﹣0.2×(﹣2.5)2+3.5,∴h=0.2(m).答:球出手时,他跳离地面的高度为0.2m.
