2022-2023学年人教版八年级数学上册12.2全等三角形判定(SAS) 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2全等三角形判定(SAS) 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 830.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 19:01:11 | ||
图片预览





文档简介
(共22张PPT)
第十二章 全等三角形
12.2 全等三角形的判定(SAS)
人教版 八年级上册
学习目标
1.知道三角形全等“边角边”的内容;
2.经历探索三角形全等条件的过程,体会利
用操作、归纳获得数学结论的过程;
3.能运用“SAS”证明简单的三角形全等问题
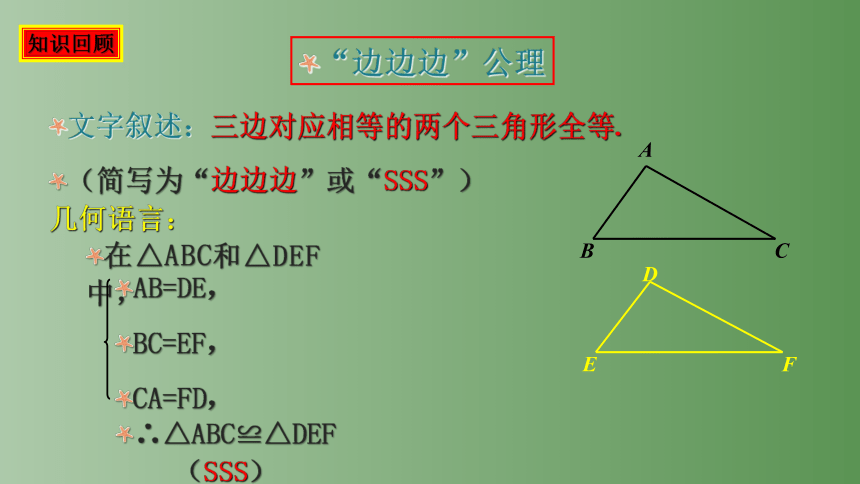
文字叙述:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
“边边边”公理
A
B
C
D
E
F
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
AB=DE,
BC=EF,
CA=FD,
几何语言:
知识回顾
情境导入
某同学不小心把一块三角形的纸片从两个顶点处撕成两块(如图),现要做一块完全一样的纸片.请问用哪一片,就能做成完全一样的纸片
①
②
两个三角形满足三个条件对应相等时是否全等
①三个角对应相等;Ⅹ
②三条边对应相等;√
③一个角和两条边对应相等?
④两个角和一条边对应相等;
昨天探究了前两种情况,今天看看第三种情况会怎样?
新知探究
动手操作
1.用三角板画∠MAN=30°;
2.在AM上截取AB=2cm;在AN上截取AC=3cm;
3.连接BC.
与本小组同学所画的△ABC的比较一下,它们全等吗?
它们全等
其它满足两边一夹角对应相等的两个三角形是否全等呢?
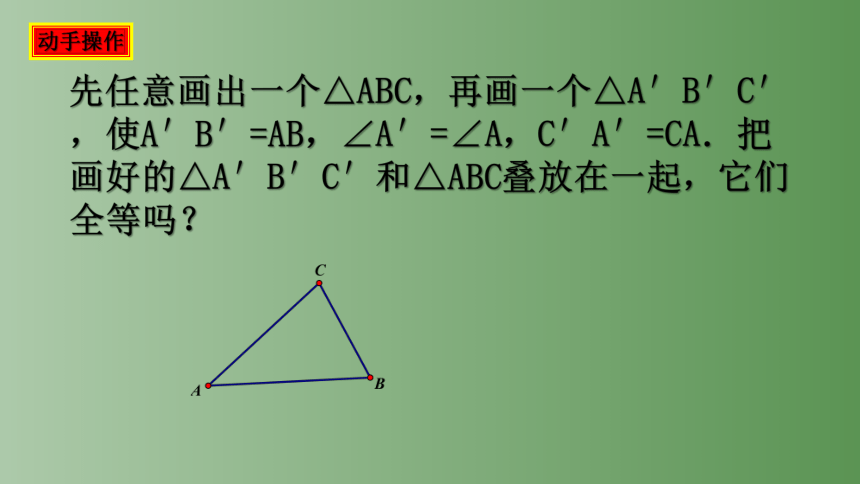
先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,C′A′=CA.把画好的△A′B′C′和△ABC叠放在一起,它们全等吗?
动手操作
动手操作
A′
D
E
C′
B′
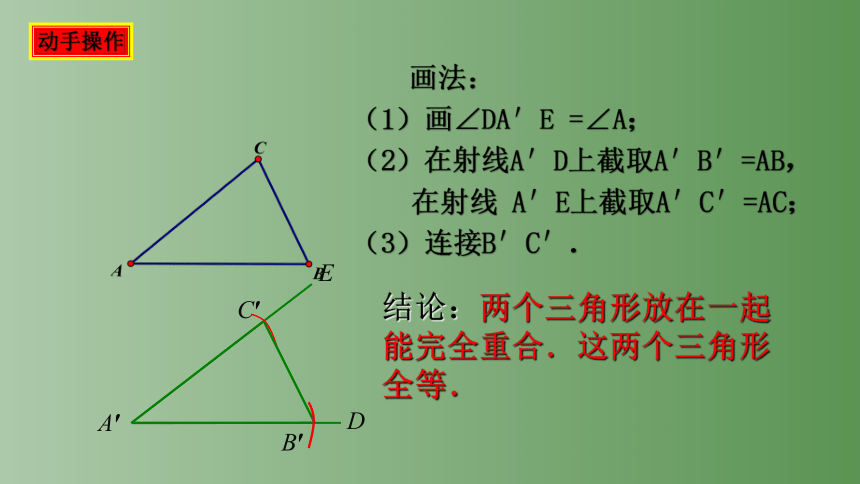
画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,
在射线 A′E上截取A′C′=AC;
(3)连接B′C′.
结论:两个三角形放在一起能完全重合.这两个三角形全等.
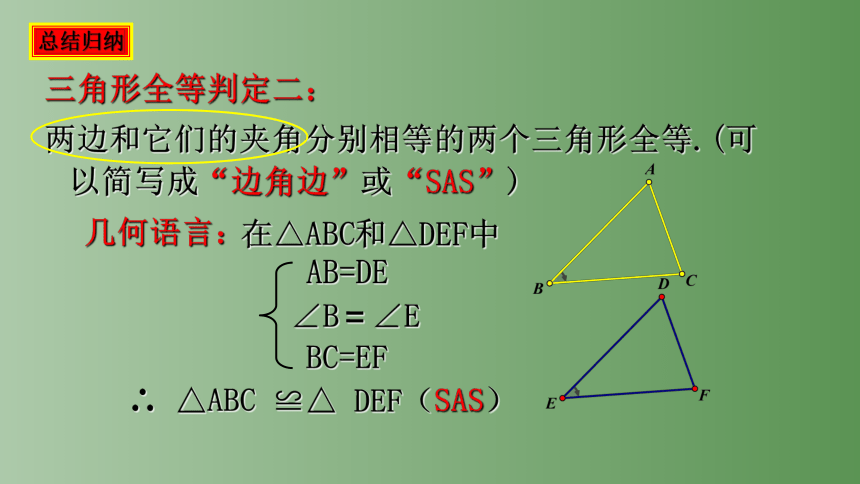
三角形全等判定二:
两边和它们的夹角分别相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
几何语言:
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SAS)
AB=DE
∠B=∠E
BC=EF
总结归纳
1.下列图形中有没有全等三角形,并说明全等的理由
跟踪练习
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
图甲与图丙全等,依据就是“SAS”.
变式训练
甲
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
图甲和图乙也满足俩边一角分别相等,从图上直接看出这俩个三角形不全等.
图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等
注意:两边和它们的夹角分别相等的两个三角形全等.
有两边和其中一边的对角分别相等的两个三角形不一定全等.没有SSA
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.
在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了
例题分析
证明:
在△ABC和△DEC中,
CA=CD(已知)
∠ACB=∠DCE(对顶角相等)
CB=CE(已知)
∴AB=DE(全等三角形对应边相等)
∴△ABC≌△DEC(SAS)
例题分析
跟踪练习
如图,点B、E、C、F在一条直线上,BE=CF,AB=DE,∠B=∠1.求证:∠A=∠D
证明:∵BE=CF
∴BE+EC=CF+EC
即BC=EF;
在△ABC和△DEF中
AB=DE
∠B=∠1
BC=EF
∴△ABC≌△DEF(SAS),
∴ ∠A=∠D
解决问题
某同学不小心把一块三角形的纸片从两个顶点处撕成两块(如图),现要做一块完全一样的纸片.请问用哪一片,就能做成完全一样的纸片
①
②
利用今天所学“边角边”知识,用纸片①,因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
边
角边
公理内容
两边和它们的夹角分别相等的两个三角形全等.(简写成“SAS”或“边角边”)
几何条理
思路分析
书写步骤
结合图形找隐含条件和已知条件,证准备条件.
注意事项
证明所用角和边必须在所证明的两个三角形中
本课小结
①准备条件
②指明范围
③摆齐条件
④写出结论
当堂检测
1.两边及其夹角分别相等的两个三角形全等.可以简写成 或 .
2.三边分别相等的两个三角形全等.可以简写成 或 .
3.如图,AB=AC,∠BAD=∠CAD,则能说明△ABD≌△ACD的依据是( )
当堂检测
A.SSS B.ASA
C.AAS D.SAS
当堂检测
4.如图,线段AC与BD相交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件可以是( )
A. ∠A=∠D B. OB=OD
C. ∠B=∠C D. AB=DC
当堂检测
5.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )
A.∠A=∠D
B.∠E=∠C
C.∠A=∠C
D.∠ABD=∠EBC
当堂检测
6.如图,AC与BD相交于点O,已知OA=OC,OB=OD,
(1)求证:△AOB≌△COD
(2)说明线段AB与CD的关系
爱 拼 才 会 赢!
第十二章 全等三角形
12.2 全等三角形的判定(SAS)
人教版 八年级上册
学习目标
1.知道三角形全等“边角边”的内容;
2.经历探索三角形全等条件的过程,体会利
用操作、归纳获得数学结论的过程;
3.能运用“SAS”证明简单的三角形全等问题
文字叙述:三边对应相等的两个三角形全等.
(简写为“边边边”或“SSS”)
“边边边”公理
A
B
C
D
E
F
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
AB=DE,
BC=EF,
CA=FD,
几何语言:
知识回顾
情境导入
某同学不小心把一块三角形的纸片从两个顶点处撕成两块(如图),现要做一块完全一样的纸片.请问用哪一片,就能做成完全一样的纸片
①
②
两个三角形满足三个条件对应相等时是否全等
①三个角对应相等;Ⅹ
②三条边对应相等;√
③一个角和两条边对应相等?
④两个角和一条边对应相等;
昨天探究了前两种情况,今天看看第三种情况会怎样?
新知探究
动手操作
1.用三角板画∠MAN=30°;
2.在AM上截取AB=2cm;在AN上截取AC=3cm;
3.连接BC.
与本小组同学所画的△ABC的比较一下,它们全等吗?
它们全等
其它满足两边一夹角对应相等的两个三角形是否全等呢?
先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A′=∠A,C′A′=CA.把画好的△A′B′C′和△ABC叠放在一起,它们全等吗?
动手操作
动手操作
A′
D
E
C′
B′
画法:
(1)画∠DA′E =∠A;
(2)在射线A′D上截取A′B′=AB,
在射线 A′E上截取A′C′=AC;
(3)连接B′C′.
结论:两个三角形放在一起能完全重合.这两个三角形全等.
三角形全等判定二:
两边和它们的夹角分别相等的两个三角形全等.(可以简写成“边角边”或“SAS”)
几何语言:
在△ABC和△DEF中
∴ △ABC ≌△ DEF(SAS)
AB=DE
∠B=∠E
BC=EF
总结归纳
1.下列图形中有没有全等三角形,并说明全等的理由
跟踪练习
甲
8 cm
9 cm
丙
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
30°
图甲与图丙全等,依据就是“SAS”.
变式训练
甲
8 cm
9 cm
8 cm
9 cm
乙
30°
30°
图甲和图乙也满足俩边一角分别相等,从图上直接看出这俩个三角形不全等.
图乙中30°的角不是已知两边的夹角,所以不与另外两个三角形全等
注意:两边和它们的夹角分别相等的两个三角形全等.
有两边和其中一边的对角分别相等的两个三角形不一定全等.没有SSA
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?
分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.
在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了
例题分析
证明:
在△ABC和△DEC中,
CA=CD(已知)
∠ACB=∠DCE(对顶角相等)
CB=CE(已知)
∴AB=DE(全等三角形对应边相等)
∴△ABC≌△DEC(SAS)
例题分析
跟踪练习
如图,点B、E、C、F在一条直线上,BE=CF,AB=DE,∠B=∠1.求证:∠A=∠D
证明:∵BE=CF
∴BE+EC=CF+EC
即BC=EF;
在△ABC和△DEF中
AB=DE
∠B=∠1
BC=EF
∴△ABC≌△DEF(SAS),
∴ ∠A=∠D
解决问题
某同学不小心把一块三角形的纸片从两个顶点处撕成两块(如图),现要做一块完全一样的纸片.请问用哪一片,就能做成完全一样的纸片
①
②
利用今天所学“边角边”知识,用纸片①,因为它完整地保留了两边及其夹角,一个三角形两条边的长度和夹角的大小确定了,这个三角形的形状、大小就确定下来了.
边
角边
公理内容
两边和它们的夹角分别相等的两个三角形全等.(简写成“SAS”或“边角边”)
几何条理
思路分析
书写步骤
结合图形找隐含条件和已知条件,证准备条件.
注意事项
证明所用角和边必须在所证明的两个三角形中
本课小结
①准备条件
②指明范围
③摆齐条件
④写出结论
当堂检测
1.两边及其夹角分别相等的两个三角形全等.可以简写成 或 .
2.三边分别相等的两个三角形全等.可以简写成 或 .
3.如图,AB=AC,∠BAD=∠CAD,则能说明△ABD≌△ACD的依据是( )
当堂检测
A.SSS B.ASA
C.AAS D.SAS
当堂检测
4.如图,线段AC与BD相交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件可以是( )
A. ∠A=∠D B. OB=OD
C. ∠B=∠C D. AB=DC
当堂检测
5.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )
A.∠A=∠D
B.∠E=∠C
C.∠A=∠C
D.∠ABD=∠EBC
当堂检测
6.如图,AC与BD相交于点O,已知OA=OC,OB=OD,
(1)求证:△AOB≌△COD
(2)说明线段AB与CD的关系
爱 拼 才 会 赢!
