2021-2022学年人教版数学七年级上册1.2.1有理数 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册1.2.1有理数 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 782.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 21:03:13 | ||
图片预览





文档简介
(共15张PPT)
1.2.1有理数
导入1.同学们回想一下,我们认识了哪些数?从小学开始,我们首先认识了正整数,后来又增加了0和正分数,在认识了负整数和负分数后,今天我们就将对数的认识扩充到有理数的范畴。活动与探究(温馨提示:规范操作、注意安全)
知识讲解
1.通过两节课的学习,我们已经将数的范围扩大了,那么你能分出下列数是什么数吗
(1)1,2,3,......;
(2) 0 零
(3)-1,-2,-3,......;
难点突破
分数(正分数和负分数)
正整数
负整数
(4)
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
2.我们将所写的数做一下分类:
正整数、0、负整数统称整数,正分数和负分数统称分数。
整数和分数统称有理数
难点突破
新知形成
活动1
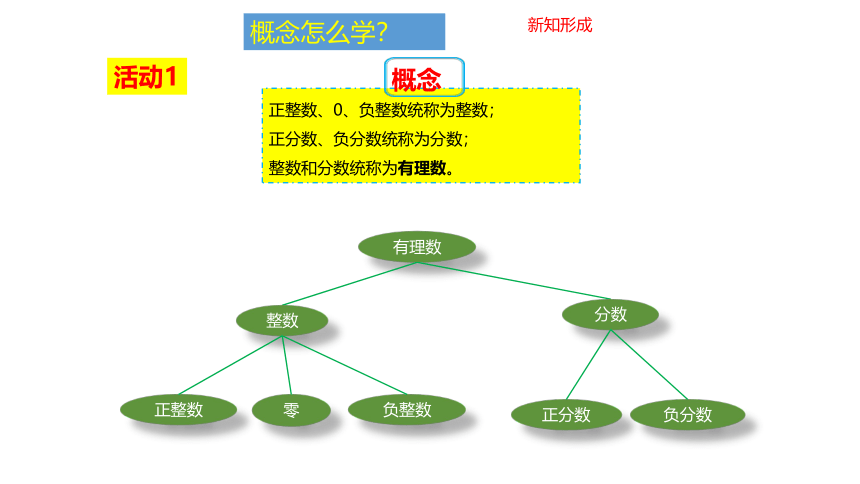
正整数、0、负整数统称为整数;
正分数、负分数统称为分数;
整数和分数统称为有理数。
概念
有理数
整数
分数
正整数
负分数
零
负整数
正分数
概念怎么学?
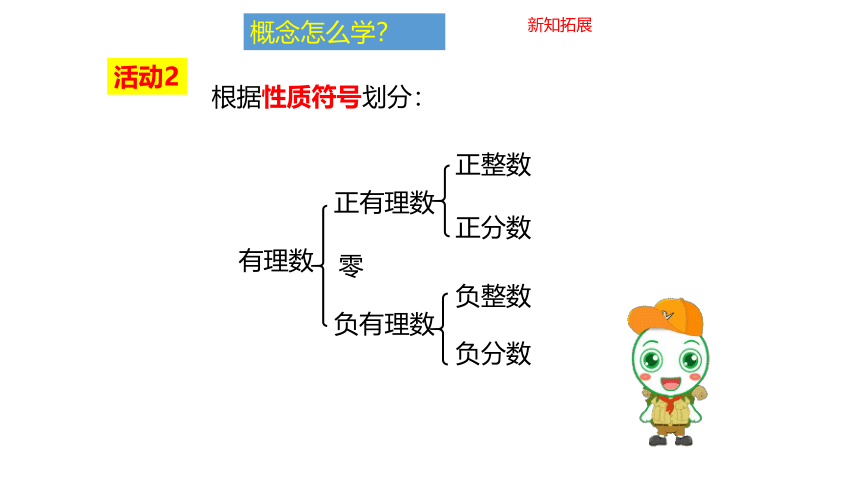
根据性质符号划分:
活动2
新知拓展
有理数
正有理数
正整数
零
负整数
正分数
负分数
负有理数
概念怎么学?
例1:依据生活情境回答下面问题:
新知应用
1.当夜空中繁星密布时,小优在数星星,他所用到的数属于什么数?
2.你日常用的直尺上,可以读出哪几类有理数?
3.测量气温用的温度计上,可以读出哪几类有理数?
正整数。
正整数、正分数、零。
正数、负数、零。
概念怎么用?
例2:把下列各数填在相应的集合中:
有理数集合:{ };
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负数集合:{ };
先化简成整数的数是整数不是分数
包括正整数和0,也称为自然数集合。
新知应用
概念怎么用?
例3:下列说法正确的是( )
①1是最小的正有理数; ②-1是最大的负有理数;
③0是最小的非负有理数;④0是最大的非正有理数。
A.①② B.②③
C.③④ D.①④
新知应用
C
注意:存在最小的正整数
概念怎么用?
例4:观察下列各组数,请找出它们的规律,并在横线上填上相应的数字。
新知应用
6
8
1
0
-1
0
14
-16
概念怎么用?
知识应用
1、把下列各数填入相应的集合内。
12/7,-3.1416,0,2008,-8/5, -0.23456,10%,10.1,0.67,-89
……
……
正数集合
负数集合
……
……
整数集合
分数集合
2008
10.1
0.67
-3.1416
-8/5
-0.23456
-89
12/7
10%
0
2008
-89
12/7
-3.1416
-8/5
-0.23456
10%
10.1
0.67
2、以下是两位同学给出的有理数的分类 方法,你认为他们的分类正确吗 ?
有理数
正有理数
负有理数
正整数
正分数
负整数
负分数
有
理
数
正数
整数
分数
负数
零
不能忘了零哦!
分类要有标准哦!
3、下列关于零的说法,正确的有 ( )
①0是最小的正整数
②0是最小的有理数
③0不是负数
④0既是非正数也是非负数
B
A、1个 B、2个
C、3个 D、4个
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
4、判 断
梳理反思
有理数的分类:
(1)按定义划分;
(2)按性质划分;
如何区分整数和分数?
如何理解非正数和非负数?
整数和分数,正数和负数之间有什么关系?
学会观察一列数字之间的规律;
进步往往从归纳反思开始!
分类的基本原则:
(1)按同一标准分类
(2)不重不漏
什么是有理数?
1.2.1有理数
导入1.同学们回想一下,我们认识了哪些数?从小学开始,我们首先认识了正整数,后来又增加了0和正分数,在认识了负整数和负分数后,今天我们就将对数的认识扩充到有理数的范畴。活动与探究(温馨提示:规范操作、注意安全)
知识讲解
1.通过两节课的学习,我们已经将数的范围扩大了,那么你能分出下列数是什么数吗
(1)1,2,3,......;
(2) 0 零
(3)-1,-2,-3,......;
难点突破
分数(正分数和负分数)
正整数
负整数
(4)
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
2.我们将所写的数做一下分类:
正整数、0、负整数统称整数,正分数和负分数统称分数。
整数和分数统称有理数
难点突破
新知形成
活动1
正整数、0、负整数统称为整数;
正分数、负分数统称为分数;
整数和分数统称为有理数。
概念
有理数
整数
分数
正整数
负分数
零
负整数
正分数
概念怎么学?
根据性质符号划分:
活动2
新知拓展
有理数
正有理数
正整数
零
负整数
正分数
负分数
负有理数
概念怎么学?
例1:依据生活情境回答下面问题:
新知应用
1.当夜空中繁星密布时,小优在数星星,他所用到的数属于什么数?
2.你日常用的直尺上,可以读出哪几类有理数?
3.测量气温用的温度计上,可以读出哪几类有理数?
正整数。
正整数、正分数、零。
正数、负数、零。
概念怎么用?
例2:把下列各数填在相应的集合中:
有理数集合:{ };
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负数集合:{ };
先化简成整数的数是整数不是分数
包括正整数和0,也称为自然数集合。
新知应用
概念怎么用?
例3:下列说法正确的是( )
①1是最小的正有理数; ②-1是最大的负有理数;
③0是最小的非负有理数;④0是最大的非正有理数。
A.①② B.②③
C.③④ D.①④
新知应用
C
注意:存在最小的正整数
概念怎么用?
例4:观察下列各组数,请找出它们的规律,并在横线上填上相应的数字。
新知应用
6
8
1
0
-1
0
14
-16
概念怎么用?
知识应用
1、把下列各数填入相应的集合内。
12/7,-3.1416,0,2008,-8/5, -0.23456,10%,10.1,0.67,-89
……
……
正数集合
负数集合
……
……
整数集合
分数集合
2008
10.1
0.67
-3.1416
-8/5
-0.23456
-89
12/7
10%
0
2008
-89
12/7
-3.1416
-8/5
-0.23456
10%
10.1
0.67
2、以下是两位同学给出的有理数的分类 方法,你认为他们的分类正确吗 ?
有理数
正有理数
负有理数
正整数
正分数
负整数
负分数
有
理
数
正数
整数
分数
负数
零
不能忘了零哦!
分类要有标准哦!
3、下列关于零的说法,正确的有 ( )
①0是最小的正整数
②0是最小的有理数
③0不是负数
④0既是非正数也是非负数
B
A、1个 B、2个
C、3个 D、4个
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
4、判 断
梳理反思
有理数的分类:
(1)按定义划分;
(2)按性质划分;
如何区分整数和分数?
如何理解非正数和非负数?
整数和分数,正数和负数之间有什么关系?
学会观察一列数字之间的规律;
进步往往从归纳反思开始!
分类的基本原则:
(1)按同一标准分类
(2)不重不漏
什么是有理数?
