24.3正多边形和圆(2)
文档属性
| 名称 | 24.3正多边形和圆(2) |  | |
| 格式 | zip | ||
| 文件大小 | 787.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-17 22:17:28 | ||
图片预览

文档简介
课件12张PPT。 数学的世界里不是缺少美,而是缺少发现和创造!
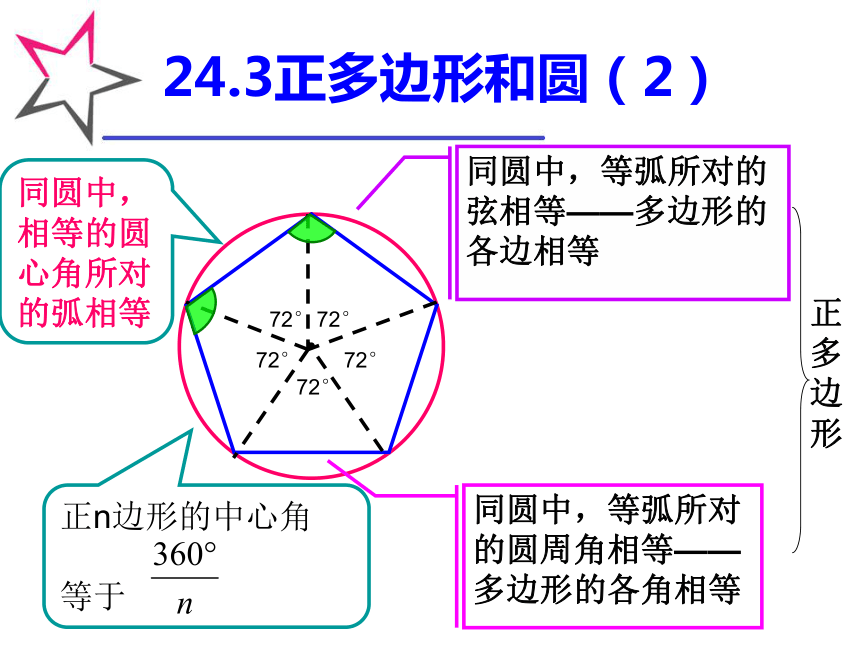
多姿多彩的正多边形●24.3正多边形和圆(2)72°同圆中,等弧所对的弦相等——多边形的各边相等同圆中,等弧所对的圆周角相等——多边形的各角相等正n边形的中心角
等于同圆中,相等的圆心角所对的弧相等·O 已知⊙O要用量角器将其六等分作它的内接正六边形。利用这种方法可以画出任意的正多边形.
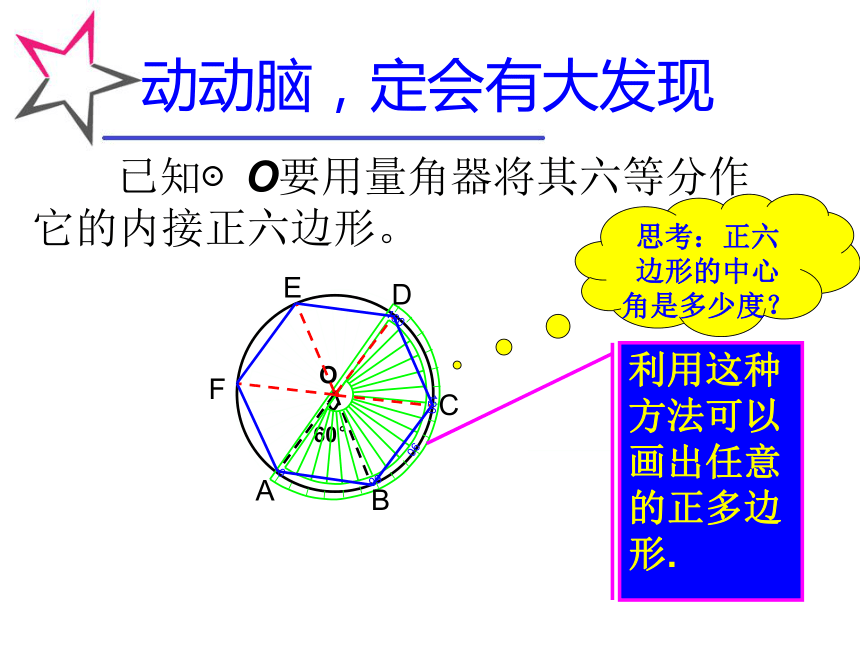
动动脑,定会有大发现思考:正六边形的中心角是多少度?·O 如图,作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧AB ,然后在圆上依次截取与这条弧AB相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
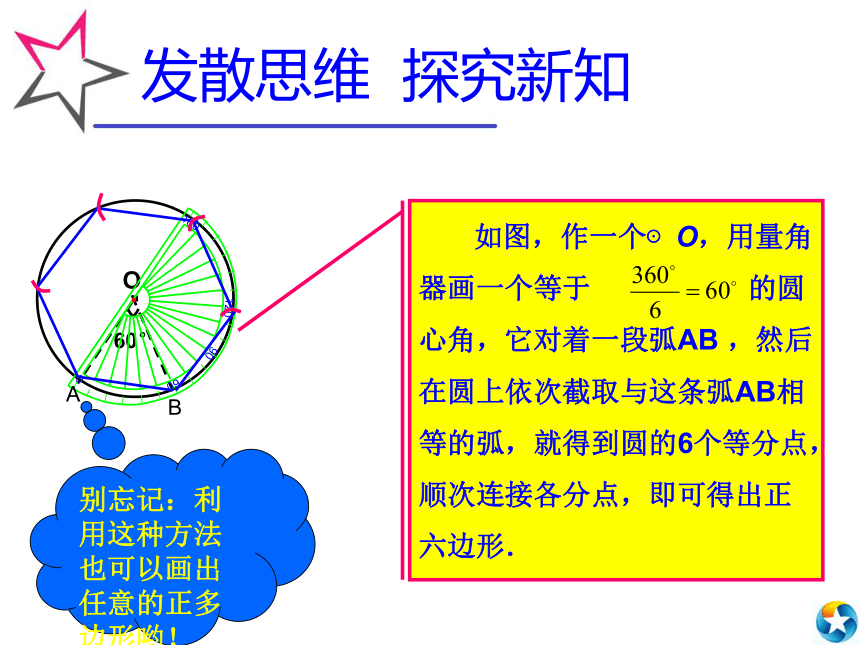
发散思维 探究新知别忘记:利用这种方法也可以画出任意的正多边形哟!
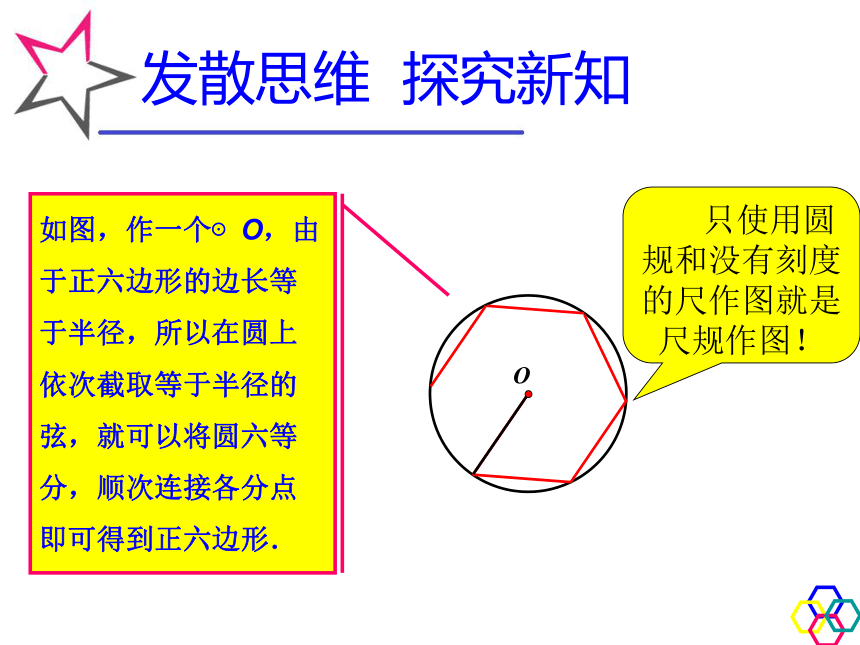
AB·O 只使用圆规和没有刻度的尺作图就是尺规作图!如图,作一个⊙O,由于正六边形的边长等于半径,所以在圆上依次截取等于半径的弦,就可以将圆六等分,顺次连接各分点即可得到正六边形.发散思维 探究新知由此,你能画出正八边吗?
你能用尺规等分圆周作正方形吗?说明作图原理.·ABCDO 只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再作各边的垂直线平分线与⊙O相交,即得圆内接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
发散思维 探究新知同理由正六边形你能继续画正几边形?
化归思想·O发散思维 探究新知用等分圆周的方法画出下列图案:学以致用 我们学校规划要在教室前的广场上建造一个圆形花坛,为了美观要在花坛内种植不同颜色的花卉.
其中关键的问题是:应该种几种,如何种才能使我们的花坛别具一格更具欣赏性!你能用本节课所学知识设计出一个方案吗?小小设计师总结归纳 畅谈收获知识
方法
反思
猜想 从下面的关键词中任选一个或几个,展示自己的演说才能,谈谈你本节课的收获或体会:交流
愉快
困惑
生活布置作业 用正多边形和圆设计一个图案,并使它有一定的寓意!
多姿多彩的正多边形●24.3正多边形和圆(2)72°同圆中,等弧所对的弦相等——多边形的各边相等同圆中,等弧所对的圆周角相等——多边形的各角相等正n边形的中心角
等于同圆中,相等的圆心角所对的弧相等·O 已知⊙O要用量角器将其六等分作它的内接正六边形。利用这种方法可以画出任意的正多边形.
动动脑,定会有大发现思考:正六边形的中心角是多少度?·O 如图,作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧AB ,然后在圆上依次截取与这条弧AB相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
发散思维 探究新知别忘记:利用这种方法也可以画出任意的正多边形哟!
AB·O 只使用圆规和没有刻度的尺作图就是尺规作图!如图,作一个⊙O,由于正六边形的边长等于半径,所以在圆上依次截取等于半径的弦,就可以将圆六等分,顺次连接各分点即可得到正六边形.发散思维 探究新知由此,你能画出正八边吗?
你能用尺规等分圆周作正方形吗?说明作图原理.·ABCDO 只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再作各边的垂直线平分线与⊙O相交,即得圆内接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
发散思维 探究新知同理由正六边形你能继续画正几边形?
化归思想·O发散思维 探究新知用等分圆周的方法画出下列图案:学以致用 我们学校规划要在教室前的广场上建造一个圆形花坛,为了美观要在花坛内种植不同颜色的花卉.
其中关键的问题是:应该种几种,如何种才能使我们的花坛别具一格更具欣赏性!你能用本节课所学知识设计出一个方案吗?小小设计师总结归纳 畅谈收获知识
方法
反思
猜想 从下面的关键词中任选一个或几个,展示自己的演说才能,谈谈你本节课的收获或体会:交流
愉快
困惑
生活布置作业 用正多边形和圆设计一个图案,并使它有一定的寓意!
同课章节目录
