12.2全等三角形的判定(4)课件(21张ppt)
文档属性
| 名称 | 12.2全等三角形的判定(4)课件(21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-16 22:06:14 | ||
图片预览






文档简介
(共21张PPT)
12.4全等三角形的判定(4)
人教版八年级上册
教学目标
1. 探索并正确理解三角形全等的判定方法“HL”.
2. 会用三角形全等的判定方法“HL”证明两个三角形全等.
新知导入
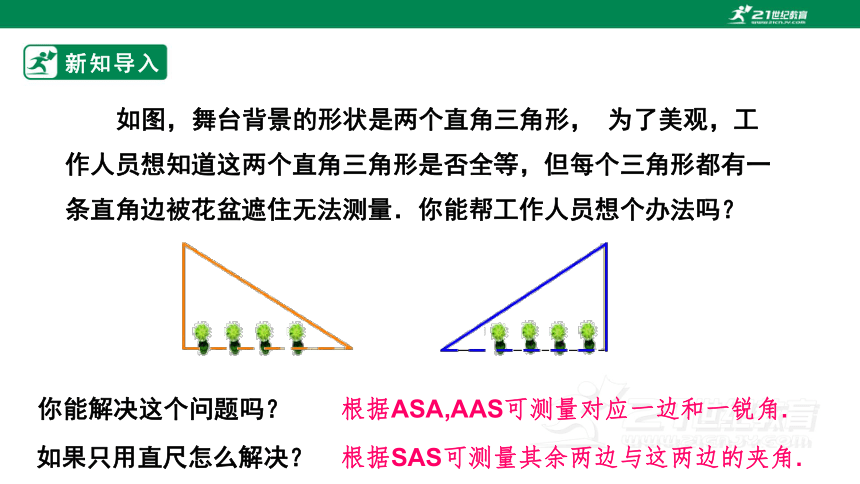
如图,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
你能解决这个问题吗?
根据SAS可测量其余两边与这两边的夹角.
根据ASA,AAS可测量对应一边和一锐角.
如果只用直尺怎么解决?
旧知回顾
SSS
SAS
ASA
AAS
我们学过的判定三角形全等的方法.
新知复习
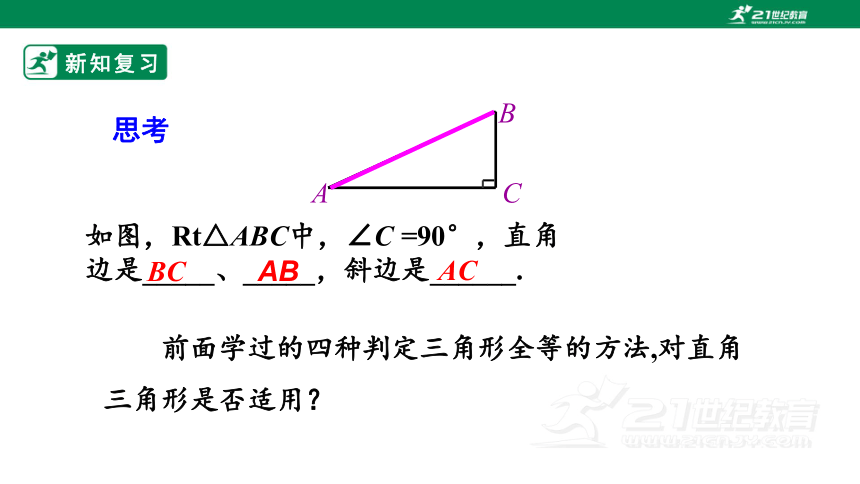
如图,Rt△ABC中,∠C =90°,直角边是_____、_____,斜边是______.
C
B
A
AC
BC
AB
思考
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
新知探究
任意画一个Rt△ABC,使∠C =90°. 再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB .然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
探究
新知探究
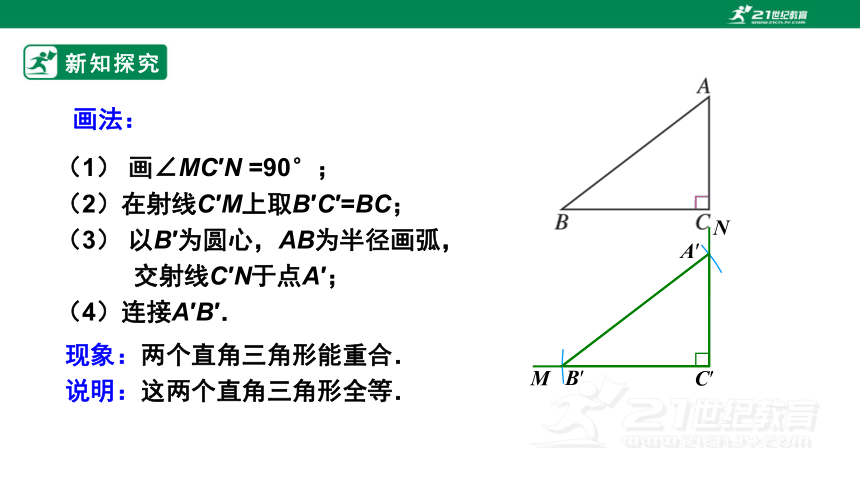
(1) 画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3) 以B′为圆心,AB为半径画弧,
交射线C′N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
N
M
C′
A′
B′
新知讲解
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
符号语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
巩固练习
2. 如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点
E ,AD、CE交于点H,已知EH=EB=3,AE=4,
则 CH的长为( )
A.1 B.2 C.3 D.4
1.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等”),根据____ (用简写法).
全等
HL
A
例题讲解
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C 和∠D 都是直角.
在Rt△ABC 和 Rt△BAD 中,
AB = BA,
AC = BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC =BD.求证 BC =AD.
练习3 如图,AC⊥BC,BD⊥AD,要明证△ABC ≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
巩固练习
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
巩固练习
练习4 如图,AB = CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE = BF.求证:AE = DF.
证明:∵CE = BF,
∴CE - EF = BF–EF,
即CF = BE.
又∵AE⊥BC,DF⊥BC,
∴∠DFC =∠AEB =90°.
在Rt△DFC与Rt△AEB中,
∴Rt△DFC≌Rt△AEB(HL).
∴AE = DF.
典例讲解
例2 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
巩固练习
练习5 如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E 两地.DA⊥AB,EB⊥AB.D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
解:D、E与路段AB的距离相等.理由:
∵C是路段AB的中点,
∴AC = BC,
又∵两人同时同速度出发,并同时到达D,E两地.
∴CD = CE,
又DA⊥AB,EB⊥AB,
∴∠A=∠B =90°,
在Rt△ACD与Rt△BCE中,
∴Rt△ACD≌Rt△BCE(HL).
∴DA = EB,
即D、E与路段AB的距离相等.
课堂总结
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
拓展提高
1. 在 Rt△ABC 和 Rt△A′B′C′ 中,∠C′=∠C=90°,∠B′=∠A,AB = B′A′,则下列结论正确的是( )
A.AC = A′C′ B.BC = B′C′
C.AC = B′C′ D.∠A′=∠A
C
拓展提高
2.如图,在△ABC中,∠BAC = 90°,AB=AC,EF是过点A的直线,BE⊥EF于E,CF⊥EF于F,试探求线段BE、CF、EF之间的关系,并加以证明.
解:BE + CF = EF,证明如下:
∵BE⊥EF,CF⊥EF,
∴∠BEA =∠AFC =90°.
又∠BAC = 90°,
∴∠EAB +∠CAF =180°-∠BAC = 90°,
∴∠EAB =∠FCA,
在△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
∴BE = AF,AE = CF,
∴BE+CF = AF+AE = EF.
拓展提高
3.如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P,Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm;
拓展提高
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm,
∴当AP=5cm或10cm时,△ABC才能和△APQ全等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.4全等三角形的判定(4)
人教版八年级上册
教学目标
1. 探索并正确理解三角形全等的判定方法“HL”.
2. 会用三角形全等的判定方法“HL”证明两个三角形全等.
新知导入
如图,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
你能解决这个问题吗?
根据SAS可测量其余两边与这两边的夹角.
根据ASA,AAS可测量对应一边和一锐角.
如果只用直尺怎么解决?
旧知回顾
SSS
SAS
ASA
AAS
我们学过的判定三角形全等的方法.
新知复习
如图,Rt△ABC中,∠C =90°,直角边是_____、_____,斜边是______.
C
B
A
AC
BC
AB
思考
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
新知探究
任意画一个Rt△ABC,使∠C =90°. 再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB .然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
探究
新知探究
(1) 画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3) 以B′为圆心,AB为半径画弧,
交射线C′N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
N
M
C′
A′
B′
新知讲解
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
符号语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
巩固练习
2. 如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点
E ,AD、CE交于点H,已知EH=EB=3,AE=4,
则 CH的长为( )
A.1 B.2 C.3 D.4
1.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等”),根据____ (用简写法).
全等
HL
A
例题讲解
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C 和∠D 都是直角.
在Rt△ABC 和 Rt△BAD 中,
AB = BA,
AC = BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC =BD.求证 BC =AD.
练习3 如图,AC⊥BC,BD⊥AD,要明证△ABC ≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
巩固练习
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
巩固练习
练习4 如图,AB = CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE = BF.求证:AE = DF.
证明:∵CE = BF,
∴CE - EF = BF–EF,
即CF = BE.
又∵AE⊥BC,DF⊥BC,
∴∠DFC =∠AEB =90°.
在Rt△DFC与Rt△AEB中,
∴Rt△DFC≌Rt△AEB(HL).
∴AE = DF.
典例讲解
例2 如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF .
∴ Rt△ABC≌Rt△DEF (HL).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
巩固练习
练习5 如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E 两地.DA⊥AB,EB⊥AB.D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
解:D、E与路段AB的距离相等.理由:
∵C是路段AB的中点,
∴AC = BC,
又∵两人同时同速度出发,并同时到达D,E两地.
∴CD = CE,
又DA⊥AB,EB⊥AB,
∴∠A=∠B =90°,
在Rt△ACD与Rt△BCE中,
∴Rt△ACD≌Rt△BCE(HL).
∴DA = EB,
即D、E与路段AB的距离相等.
课堂总结
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等.
前提条件
在直角三角形中
使用方法
只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
拓展提高
1. 在 Rt△ABC 和 Rt△A′B′C′ 中,∠C′=∠C=90°,∠B′=∠A,AB = B′A′,则下列结论正确的是( )
A.AC = A′C′ B.BC = B′C′
C.AC = B′C′ D.∠A′=∠A
C
拓展提高
2.如图,在△ABC中,∠BAC = 90°,AB=AC,EF是过点A的直线,BE⊥EF于E,CF⊥EF于F,试探求线段BE、CF、EF之间的关系,并加以证明.
解:BE + CF = EF,证明如下:
∵BE⊥EF,CF⊥EF,
∴∠BEA =∠AFC =90°.
又∠BAC = 90°,
∴∠EAB +∠CAF =180°-∠BAC = 90°,
∴∠EAB =∠FCA,
在△ABE和△CAF中,
∴△ABE≌△CAF(AAS).
∴BE = AF,AE = CF,
∴BE+CF = AF+AE = EF.
拓展提高
3.如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P,Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm;
拓展提高
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm,
∴当AP=5cm或10cm时,△ABC才能和△APQ全等.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
