2022—2023学年人教版数学八年级上册11.2.1三角形的内角 课件 (共15张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.2.1三角形的内角 课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 810.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
11.2.1三角形的内角
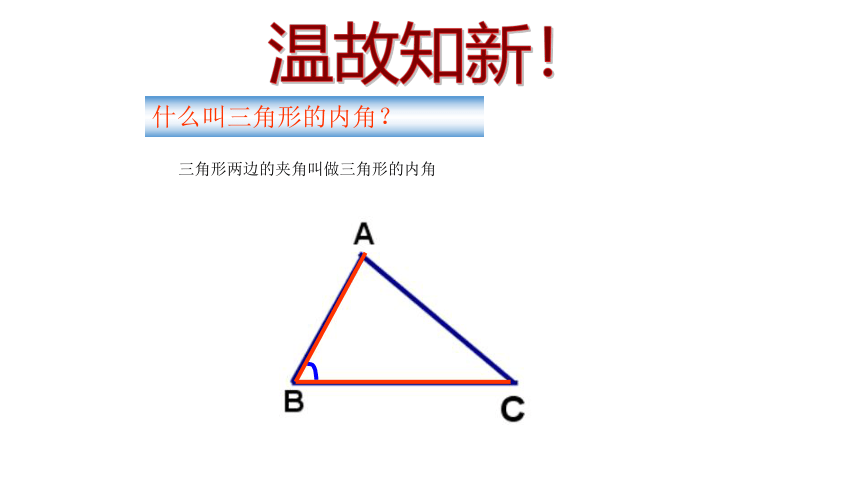
三角形两边的夹角叫做三角形的内角
什么叫三角形的内角?
温故知新!
三角形的三个内角和是多少
把三个角拼在一起试试看?
你有什么办法可以验证呢
180°
实验操作!
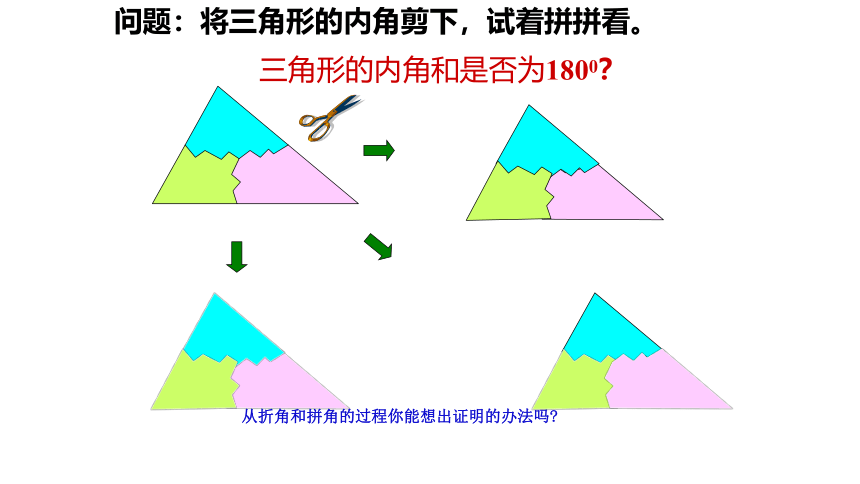
问题:将三角形的内角剪下,试着拼拼看。
三角形的内角和是否为1800?
从折角和拼角的过程你能想出证明的办法吗
自学、合作、交流!
自学课本P11-12,讨论解决以下问题:
1、三角形内角和为什么等于180°?你能想出几种方法证明三角形的内角和等于180°?
(小组合作解决)
2、看懂P12例1、例2。
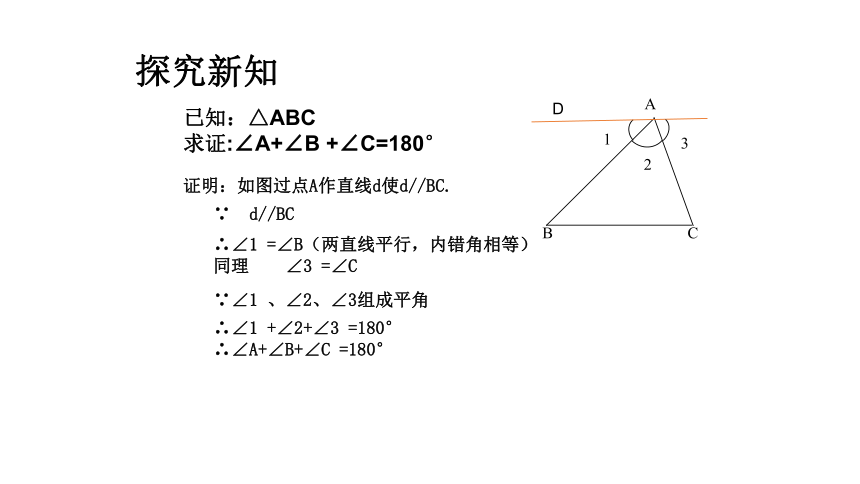
探究新知
已知:△ABC
求证:∠A+∠B +∠C=180°
A
B
C
1
2
3
证明:如图过点A作直线d使d//BC.
∵ d//BC
∴∠1 =∠B(两直线平行,内错角相等)
同理 ∠3 =∠C
∵∠1 、∠2、∠3组成平角
∴∠1 +∠2+∠3 =180°
∴∠A+∠B+∠C =180°
D
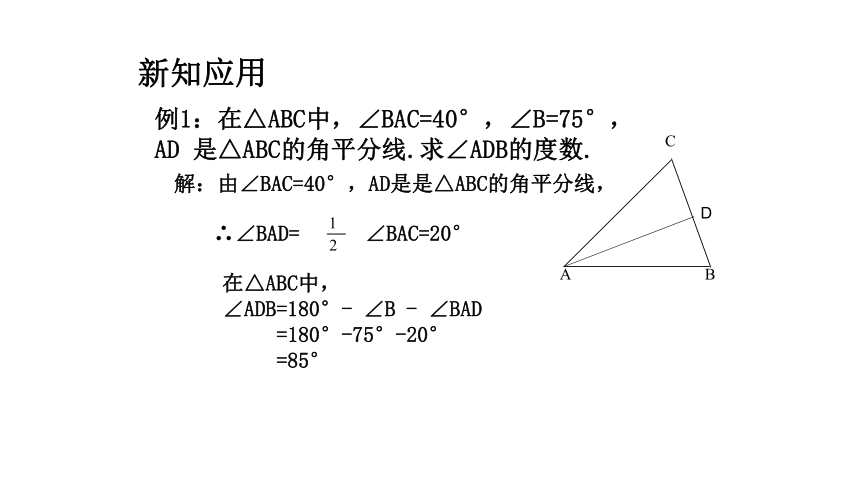
新知应用
例1:在△ABC中,∠BAC=40°,∠B=75°,
AD 是△ABC的角平分线.求∠ADB的度数.
C
A
B
D
解:由∠BAC=40°,AD是是△ABC的角平分线,
∴∠BAD= ∠BAC=20°
在△ABC中,
∠ADB=180°- ∠B - ∠BAD
=180°-75°-20°
=85°
练习1.说出下列各图中的x值.
练习2:下列各组角中哪三个角是同一个三角形的内角?
(1)70°,60°,30°,80°;
(2)110°,20°,50°,40°;
(3)52°, 32°,58°,90°;
(4)36°,108°,36°,72°.
练习3:如图,从A处观测C处时仰角∠CAD =30°,从B 处观测C处时仰角∠CBD=45°,从C处观测A,B两处时视角∠ACB是多少度?
练习1:
(1)一个三角形最多有几个直角,为什么?
(2)一个三角形最多有几个钝角,为什么?
(3)一个三角形至少有几个锐角,为什么?
练习2:已知等腰三角形的两个底角相等,则
(1)如果顶角为80°,那么它的一个底角等于多少度?
(2)如果它的一个角为80°,那么它的一个底角等于多少度?
,
练习3:如图,已知∠1=15°,∠2=30°,∠A=50°,求∠BDC的度数。
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
E
C
D
A
B
1
2
解:∵AB//CD
∴∠ABD+∠BDC=180°
∵BE平分∠ABD,DE平分∠BDC
∴∠1= ∠ABD ,
∠2=
∴ ∠1+ ∠2= (∠ABD+∠BDC)=90°
在△BED中,
∠1+ ∠2+∠E=180°
∴∠E= 180°- 90°=90°.
拓广探索
∠BDC
重点探究了三角形3个内角之间的
关系
三角形3个内角的和等于180°.
课 堂 小 结
11.2.1三角形的内角
三角形两边的夹角叫做三角形的内角
什么叫三角形的内角?
温故知新!
三角形的三个内角和是多少
把三个角拼在一起试试看?
你有什么办法可以验证呢
180°
实验操作!
问题:将三角形的内角剪下,试着拼拼看。
三角形的内角和是否为1800?
从折角和拼角的过程你能想出证明的办法吗
自学、合作、交流!
自学课本P11-12,讨论解决以下问题:
1、三角形内角和为什么等于180°?你能想出几种方法证明三角形的内角和等于180°?
(小组合作解决)
2、看懂P12例1、例2。
探究新知
已知:△ABC
求证:∠A+∠B +∠C=180°
A
B
C
1
2
3
证明:如图过点A作直线d使d//BC.
∵ d//BC
∴∠1 =∠B(两直线平行,内错角相等)
同理 ∠3 =∠C
∵∠1 、∠2、∠3组成平角
∴∠1 +∠2+∠3 =180°
∴∠A+∠B+∠C =180°
D
新知应用
例1:在△ABC中,∠BAC=40°,∠B=75°,
AD 是△ABC的角平分线.求∠ADB的度数.
C
A
B
D
解:由∠BAC=40°,AD是是△ABC的角平分线,
∴∠BAD= ∠BAC=20°
在△ABC中,
∠ADB=180°- ∠B - ∠BAD
=180°-75°-20°
=85°
练习1.说出下列各图中的x值.
练习2:下列各组角中哪三个角是同一个三角形的内角?
(1)70°,60°,30°,80°;
(2)110°,20°,50°,40°;
(3)52°, 32°,58°,90°;
(4)36°,108°,36°,72°.
练习3:如图,从A处观测C处时仰角∠CAD =30°,从B 处观测C处时仰角∠CBD=45°,从C处观测A,B两处时视角∠ACB是多少度?
练习1:
(1)一个三角形最多有几个直角,为什么?
(2)一个三角形最多有几个钝角,为什么?
(3)一个三角形至少有几个锐角,为什么?
练习2:已知等腰三角形的两个底角相等,则
(1)如果顶角为80°,那么它的一个底角等于多少度?
(2)如果它的一个角为80°,那么它的一个底角等于多少度?
,
练习3:如图,已知∠1=15°,∠2=30°,∠A=50°,求∠BDC的度数。
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
E
C
D
A
B
1
2
解:∵AB//CD
∴∠ABD+∠BDC=180°
∵BE平分∠ABD,DE平分∠BDC
∴∠1= ∠ABD ,
∠2=
∴ ∠1+ ∠2= (∠ABD+∠BDC)=90°
在△BED中,
∠1+ ∠2+∠E=180°
∴∠E= 180°- 90°=90°.
拓广探索
∠BDC
重点探究了三角形3个内角之间的
关系
三角形3个内角的和等于180°.
课 堂 小 结
