人教版八年级上册11.3.1 多边形 课件 (共14张PPT)
文档属性
| 名称 | 人教版八年级上册11.3.1 多边形 课件 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 989.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
11.3.1 多边形
什么叫做三角形?
由三条线段首尾顺次相接组成的平面图形称为三角形,又叫做三边形。
那么把定义中的三条线段换成四条、五条、六条又叫做什么呢?
问题你能从这些图形中想像出几个由一些线段围成的图形吗?
了解一下
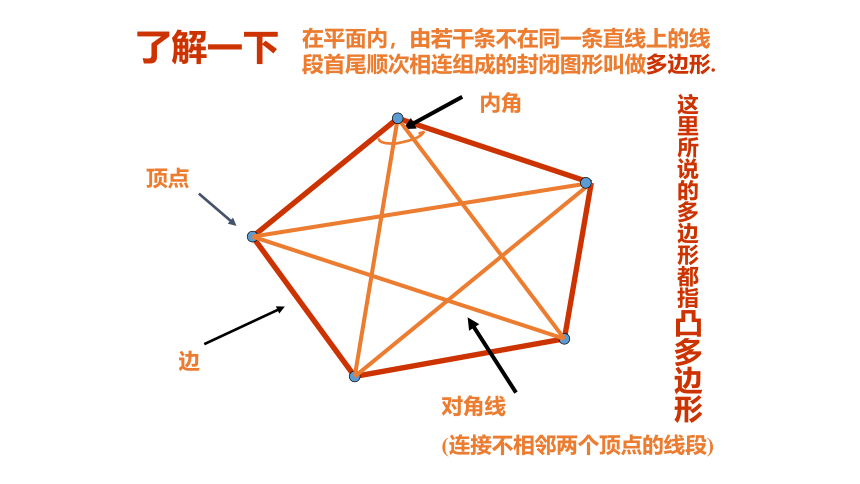
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
这里所说的多边形都指凸多边形
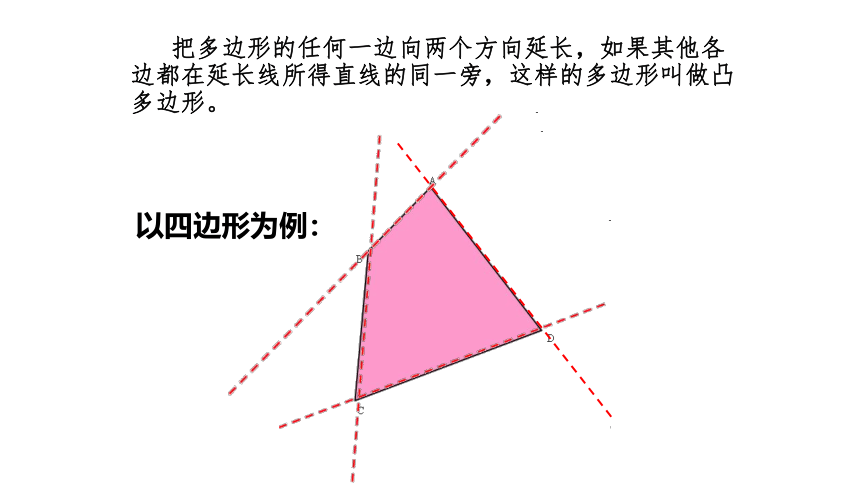
把多边形的任何一边向两个方向延长,如果其他各边都在延长线所得直线的同一旁,这样的多边形叫做凸多边形。
以四边形为例:
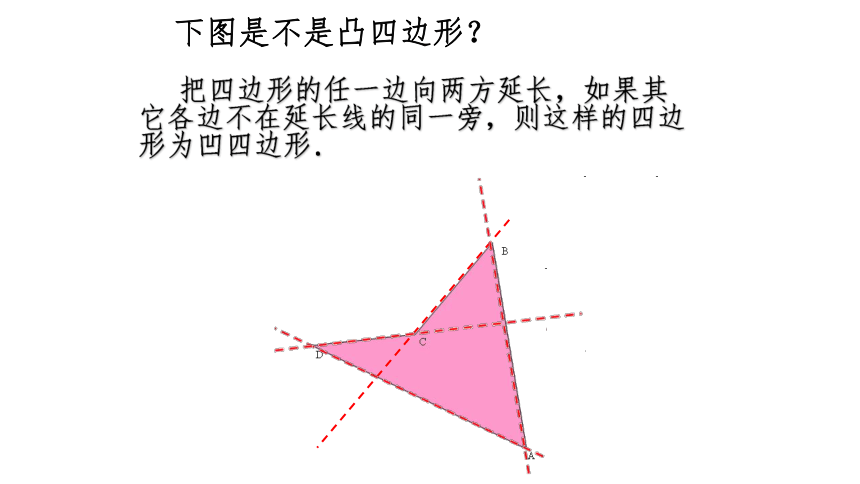
下图是不是凸四边形?
把四边形的任一边向两方延长,如果其它各边不在延长线的同一旁,则这样的四边形为凹四边形.
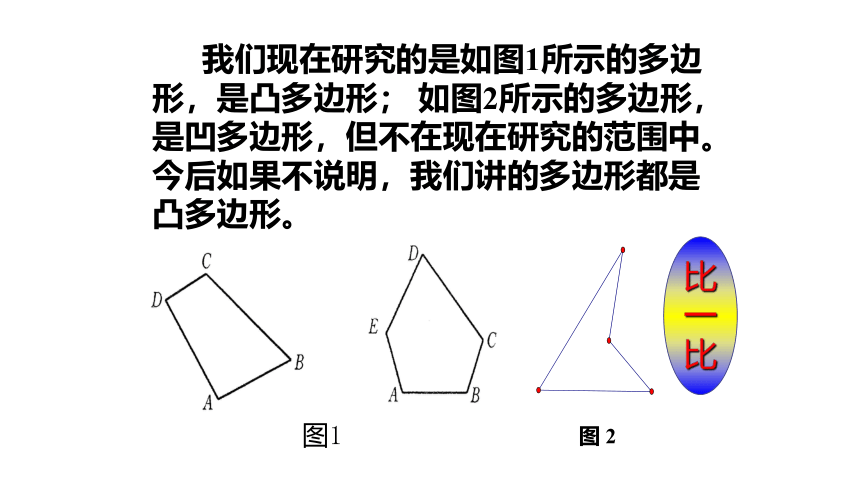
我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
图 2
比
一
比
图1
看一看
四边形
五边形
六边形
八边形
……
A
B
C
D
E
想一想
我们知道,三角形的内角和是 度,四边形的内角和是 度,那这个五边形的内角和呢?
小明利用下图求出了五边形的内角和,你知道他是怎么做的吗?
180
360
180 × 3 = 540
你能动手做一做吗
n边形有_____个顶点,_____条边,_____个内角,_____个外角,_____条对角线。总结1nnn2n 观察正三角形、正方形的特征, 猜想满足什么条件的多边形是
正多边形?
定义: 如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
1. 如果一个多边形的各边都相等,那么它是正多边形;
2. 如果一个多边形的所有内角都相等,那么它是正多边形;
下列说法正确吗?如果不正确,你能用一个例子作出
说明吗?
菱形
长方形
例 画出下列图形的所有对角线,并完成表格.
n-3
多边形的边数 3 4 5 6 … n
从一个顶点出发所有的对角线(条) …
从一个顶点出发分成三角形(个) …
对角线总数(条) …
0
1
2
3
1
2
3
4
n-2
0
2
5
9
巩固练习
2.(1)十边形有____条对角线.
(2)一个多边形自一个顶点出发的对
角线把它分成6个三角形,则它是__边形.
1. 教材第21页练习第1、2题.
(3)下列图形哪些是凸多边形,哪些不是?
11.3.1 多边形
什么叫做三角形?
由三条线段首尾顺次相接组成的平面图形称为三角形,又叫做三边形。
那么把定义中的三条线段换成四条、五条、六条又叫做什么呢?
问题你能从这些图形中想像出几个由一些线段围成的图形吗?
了解一下
在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
顶点
内角
边
对角线
(连接不相邻两个顶点的线段)
这里所说的多边形都指凸多边形
把多边形的任何一边向两个方向延长,如果其他各边都在延长线所得直线的同一旁,这样的多边形叫做凸多边形。
以四边形为例:
下图是不是凸四边形?
把四边形的任一边向两方延长,如果其它各边不在延长线的同一旁,则这样的四边形为凹四边形.
我们现在研究的是如图1所示的多边形,是凸多边形; 如图2所示的多边形,是凹多边形,但不在现在研究的范围中。今后如果不说明,我们讲的多边形都是凸多边形。
图 2
比
一
比
图1
看一看
四边形
五边形
六边形
八边形
……
A
B
C
D
E
想一想
我们知道,三角形的内角和是 度,四边形的内角和是 度,那这个五边形的内角和呢?
小明利用下图求出了五边形的内角和,你知道他是怎么做的吗?
180
360
180 × 3 = 540
你能动手做一做吗
n边形有_____个顶点,_____条边,_____个内角,_____个外角,_____条对角线。总结1nnn2n 观察正三角形、正方形的特征, 猜想满足什么条件的多边形是
正多边形?
定义: 如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
1. 如果一个多边形的各边都相等,那么它是正多边形;
2. 如果一个多边形的所有内角都相等,那么它是正多边形;
下列说法正确吗?如果不正确,你能用一个例子作出
说明吗?
菱形
长方形
例 画出下列图形的所有对角线,并完成表格.
n-3
多边形的边数 3 4 5 6 … n
从一个顶点出发所有的对角线(条) …
从一个顶点出发分成三角形(个) …
对角线总数(条) …
0
1
2
3
1
2
3
4
n-2
0
2
5
9
巩固练习
2.(1)十边形有____条对角线.
(2)一个多边形自一个顶点出发的对
角线把它分成6个三角形,则它是__边形.
1. 教材第21页练习第1、2题.
(3)下列图形哪些是凸多边形,哪些不是?
