2022-2023学年人教版八年级数学上册12.2.2 三角形全等的判定SAS 课件 (共15张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2.2 三角形全等的判定SAS 课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 917.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 11:38:10 | ||
图片预览


文档简介
(共15张PPT)
12.2.2 三角形全等的判定SAS
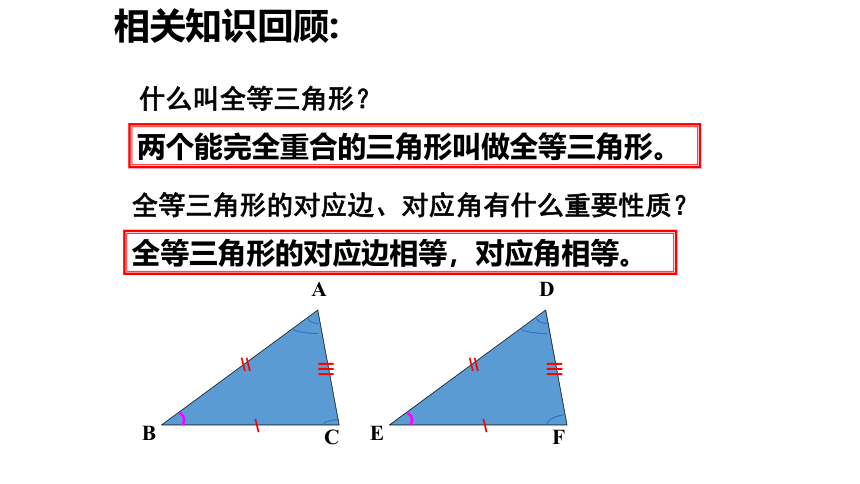
全等三角形的对应边相等,对应角相等。
全等三角形的对应边、对应角有什么重要性质?
两个能完全重合的三角形叫做全等三角形。
什么叫全等三角形?
相关知识回顾:
\\
\
A
B
C
\\
\
D
E
F
情境问题一:
家里衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让我到玻璃店配一块回来, 该怎么办才能做到呢
归纳总结,继续探究:
确定一个三角形的形状,大小至少需要三个元素,确定三角形形状,大小的条件能否作为判断三角形全等的条件呢?
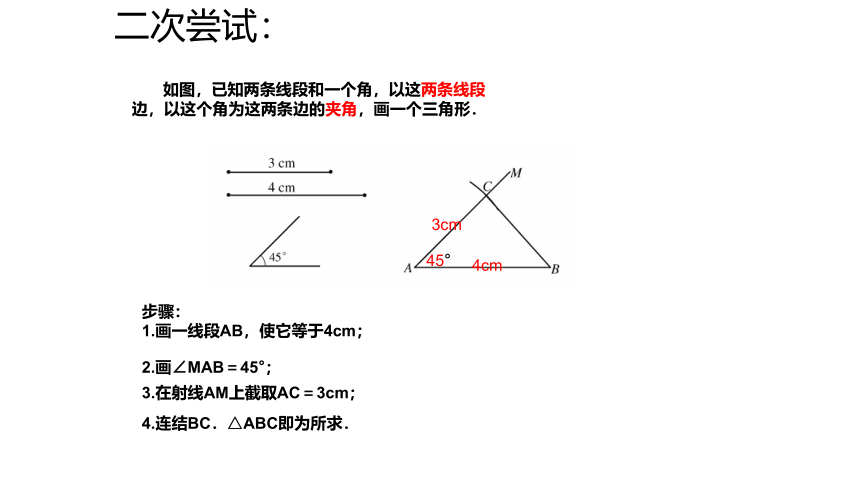
如图,已知两条线段和一个角,以这两条线段
边,以这个角为这两条边的夹角,画一个三角形.
步骤:
1.画一线段AB,使它等于4cm;
4cm
45°
3cm
2.画∠MAB=45°;
3.在射线AM上截取AC=3cm;
4.连结BC.△ABC即为所求.
二次尝试:
A
B
C
D
E
F
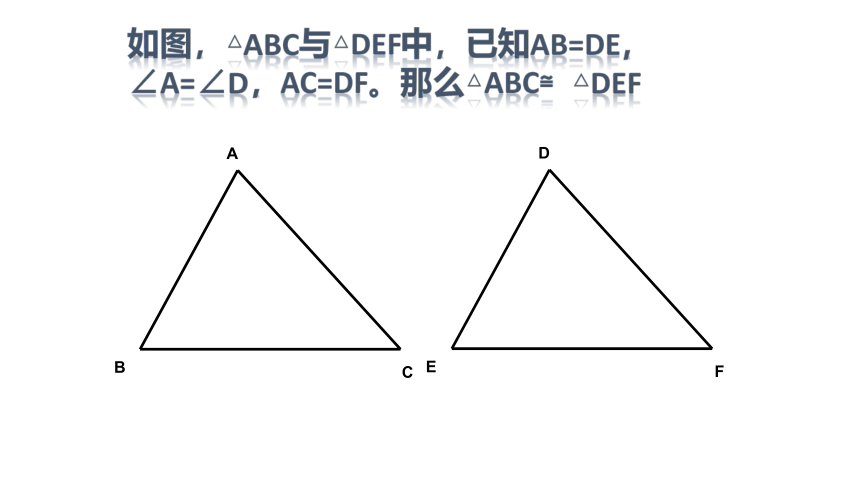
如图,△abc与△def中,已知ab=de,∠a=∠d,ac=df。那么△abc≌△def
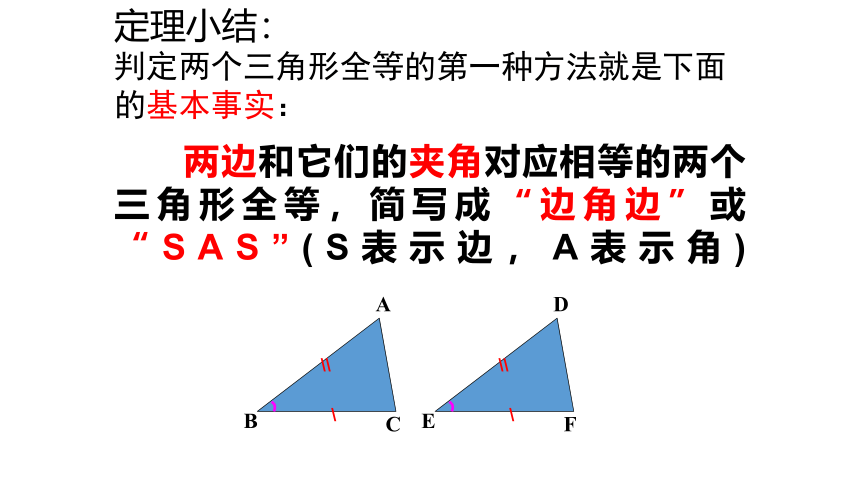
判定两个三角形全等的第一种方法就是下面
的基本事实:
\\
\
A
B
C
\\
\
D
E
F
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”(S表示边,A表示角)
定理小结:
14.2 三角形全等的判定
4
4
练一练:
1.如图,在下列三角形中,哪两个三角形全等
4
4
5
5
30°
30°
4
4
30°
4
6
40°
4
6
40°
40°
①
③
②
⑥
⑤
④
2.在下列图中找出全等三角形,并把它们用直线连起来.
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
Ⅲ
8 cm
Ⅱ
5 cm
30
已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA
分析:观察图形,结合已知条件,知,
AD=CB,AC=CA,但没有给出两组对应边的夹角(∠1,∠2)相等。
所以,应设法先证明∠1=∠2,才能使全等条件充足。
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)
例1:
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
B
2
B
例2: 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结DE,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC
∠ACB=∠DCE
BC=EC
∴△ACB≌△DCE
∴AB=DE
在△ACB和△DCE中
1: 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △ OAD与
△ OBC全等的理由
OA = OB(已知)
∠1 =∠2(对顶角相等)
OD = OC (已知)
∴△OAD≌△OBC (S.A.S)
解:在△OAD 和△OBC中
C
B
A
D
O
2
1
巩固练习
2. 如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:
(1)全等
(2)全等
巩固练习
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
探索“SSA”能否识别两三角形全等
问题3 两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
12.2.2 三角形全等的判定SAS
全等三角形的对应边相等,对应角相等。
全等三角形的对应边、对应角有什么重要性质?
两个能完全重合的三角形叫做全等三角形。
什么叫全等三角形?
相关知识回顾:
\\
\
A
B
C
\\
\
D
E
F
情境问题一:
家里衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让我到玻璃店配一块回来, 该怎么办才能做到呢
归纳总结,继续探究:
确定一个三角形的形状,大小至少需要三个元素,确定三角形形状,大小的条件能否作为判断三角形全等的条件呢?
如图,已知两条线段和一个角,以这两条线段
边,以这个角为这两条边的夹角,画一个三角形.
步骤:
1.画一线段AB,使它等于4cm;
4cm
45°
3cm
2.画∠MAB=45°;
3.在射线AM上截取AC=3cm;
4.连结BC.△ABC即为所求.
二次尝试:
A
B
C
D
E
F
如图,△abc与△def中,已知ab=de,∠a=∠d,ac=df。那么△abc≌△def
判定两个三角形全等的第一种方法就是下面
的基本事实:
\\
\
A
B
C
\\
\
D
E
F
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”(S表示边,A表示角)
定理小结:
14.2 三角形全等的判定
4
4
练一练:
1.如图,在下列三角形中,哪两个三角形全等
4
4
5
5
30°
30°
4
4
30°
4
6
40°
4
6
40°
40°
①
③
②
⑥
⑤
④
2.在下列图中找出全等三角形,并把它们用直线连起来.
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
Ⅲ
8 cm
Ⅱ
5 cm
30
已知:如图,AD∥BC,AD=CB
求证:△ADC≌△CBA
分析:观察图形,结合已知条件,知,
AD=CB,AC=CA,但没有给出两组对应边的夹角(∠1,∠2)相等。
所以,应设法先证明∠1=∠2,才能使全等条件充足。
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴△ADC≌△CBA(SAS)
例1:
证明:∵AD∥BC
∴∠1=∠2(两直线平行,内错角相等)
在△DAC和△BCA中
D
C
1
A
B
2
B
例2: 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结DE,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC
∠ACB=∠DCE
BC=EC
∴△ACB≌△DCE
∴AB=DE
在△ACB和△DCE中
1: 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △ OAD与
△ OBC全等的理由
OA = OB(已知)
∠1 =∠2(对顶角相等)
OD = OC (已知)
∴△OAD≌△OBC (S.A.S)
解:在△OAD 和△OBC中
C
B
A
D
O
2
1
巩固练习
2. 如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC=DF, ∠C=∠F, BC=EF;
(2) BC=BD, ∠ABC=∠ABD.
答案:
(1)全等
(2)全等
巩固练习
如图,在△ABC 和△ABD 中,
AB =AB,AC = AD,∠B =∠B,
但△ABC 和△ABD 不全等.
探索“SSA”能否识别两三角形全等
问题3 两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
