2022-2023学年人教版八年级数学上册12.3 角的平分线的性质 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.3 角的平分线的性质 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 891.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
12.3 角的平分线的性质
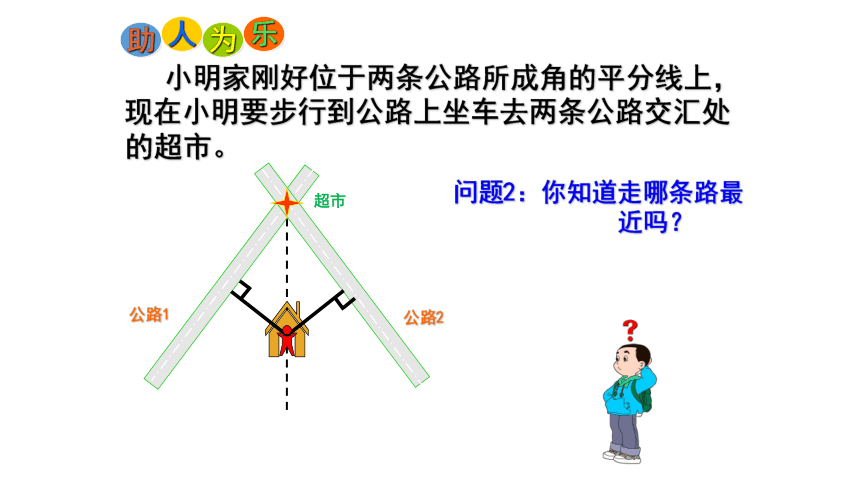
小明家刚好位于两条公路所成角的平分线上,现在小明要步行到公路上坐车去两条公路交汇处的超市。
助
人
为
乐
公路2
公路1
问题2:你知道走哪条路最
近吗?
超市
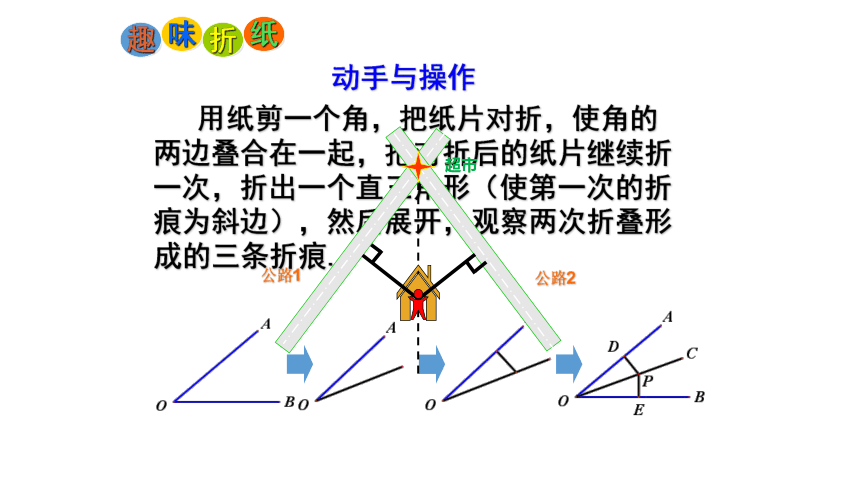
用纸剪一个角,把纸片对折,使角的两边叠合在一起,把对折后的纸片继续折一次,折出一个直三角形(使第一次的折痕为斜边),然后展开,观察两次折叠形成的三条折痕.
动手与操作
趣
味
折
纸
公路2
公路1
超市
=
数
据
收
集
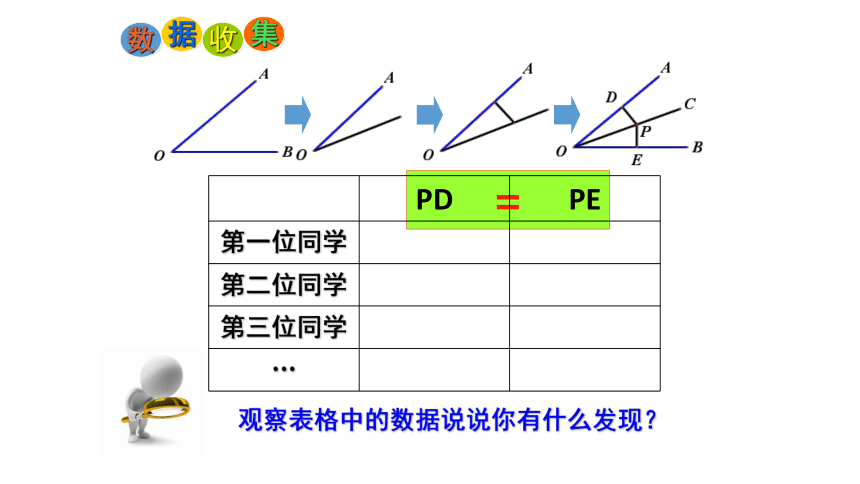
PD PE
第一位同学
第二位同学
第三位同学
…
观察表格中的数据说说你有什么发现?
重
大
发
现
角的平分线上的点到角的两边的距离相等。
当真如此吗?
公路2
公路1
超市
验
证
猜
想
几何模型
2
1
O
A
B
P
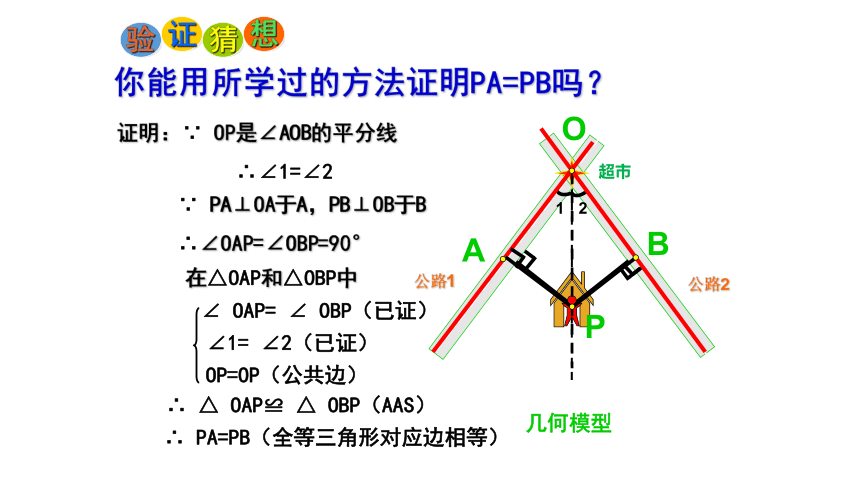
你能用所学过的方法证明PA=PB吗?
证明:∵ OP是∠AOB的平分线
∴∠1=∠2
在△OAP和△OBP中
∠1= ∠2(已证)
∴ △ OAP≌ △ OBP(AAS)
∴ PA=PB(全等三角形对应边相等)
∵ PA⊥OA于A,PB⊥OB于B
∴∠OAP=∠OBP=90°
∠ OAP= ∠ OBP(已证)
OP=OP(公共边)
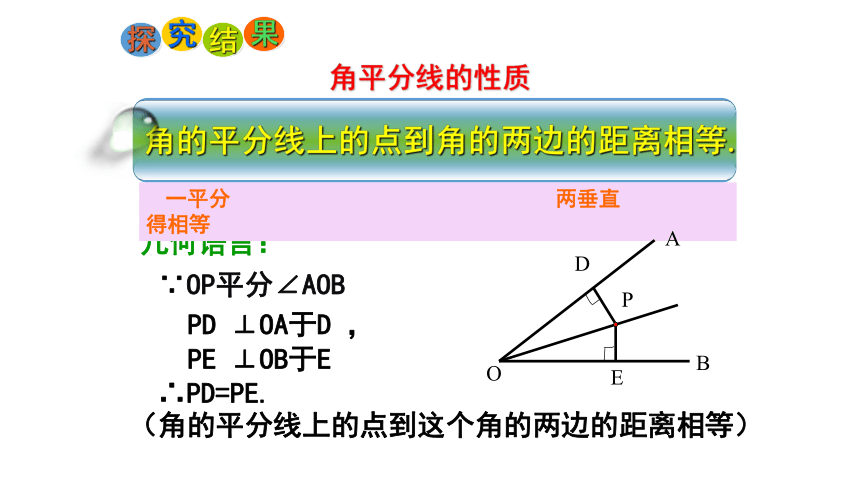
探
究
结
果
角的平分线上的点到角的两边的距离相等.
角平分线的性质
PD ⊥OA于D ,
PE ⊥OB于E
∵OP平分∠AOB
∴PD=PE.
几何语言:
一平分 两垂直 得相等
(角的平分线上的点到这个角的两边的距离相等)
A
O
B
P
E
D
角平分线有什么性质?
猜一猜
角平分线线上的点到角的两边的距离相等。
通过动手实验、观察比较,我们发现“角的平分线上的点到角的两边的距离相等”,你能通过严格的逻辑推理证明这个结论吗?
已知:∠AOC = ∠BOC,点P在OC上,
PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD =PE.
A
B
O
P
C
D
E
证一证
已知:∠AOC= ∠BOC ,点P在OC上,PD⊥OA于D,
PE⊥OB于E.
求证: PD=PE.
O
A
B
E
D
P
C
∵ PD⊥OA,PE⊥OB
证明:
∴ ∠PDO= ∠PEO= 90°
在△POD 和 △PEO 中
∴ △PDO ≌△PEO(AAS)
∠ PDO=∠PEO
∠ AOC=∠BOC
OP=OP
∴ PD=PE
由角的平分线的性质的证明过程,你能概
括出证明几何命题的一般步骤吗?
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用数学符号
表示已知和求证;
(3)经过分析,找出由已知推出求证的途
径,写出证明过程.
归纳
角的平分线的性质的作用是什么?
主要是用于判断和证明两条线段相等,与以
前的方法相比,运用此性质不需要先证两个三角
形全等.
思考
例题学习
例 如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F.
∴PD=PE.
同理PE=PF.
∴PD=PE=PF
即点P到三边AB、BC、CA的距离相等.
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1︰20000)
解决问题
S
公路
铁路
已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
◆证明: ∵AD平分∠CAB
DE⊥AB ,DF⊥AC(已知)
∴DE=DF (角平分线的性质)
在Rt△BED和Rt△CFD中,
BD=CD (已证)
DE=DF (已知)
∴ Rt△ BED ≌Rt△CFD (HL)
∴ BE=FC (全等三角形对应边相等)
回味无穷
性质 角平分线上的点到这个角的两边距离相等.
几何语言:
∵OC是∠AOB的平分线,
P是OC上任意一点 PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
课堂 小结
P
A
O
B
C
E
D
1
2
12.3 角的平分线的性质
小明家刚好位于两条公路所成角的平分线上,现在小明要步行到公路上坐车去两条公路交汇处的超市。
助
人
为
乐
公路2
公路1
问题2:你知道走哪条路最
近吗?
超市
用纸剪一个角,把纸片对折,使角的两边叠合在一起,把对折后的纸片继续折一次,折出一个直三角形(使第一次的折痕为斜边),然后展开,观察两次折叠形成的三条折痕.
动手与操作
趣
味
折
纸
公路2
公路1
超市
=
数
据
收
集
PD PE
第一位同学
第二位同学
第三位同学
…
观察表格中的数据说说你有什么发现?
重
大
发
现
角的平分线上的点到角的两边的距离相等。
当真如此吗?
公路2
公路1
超市
验
证
猜
想
几何模型
2
1
O
A
B
P
你能用所学过的方法证明PA=PB吗?
证明:∵ OP是∠AOB的平分线
∴∠1=∠2
在△OAP和△OBP中
∠1= ∠2(已证)
∴ △ OAP≌ △ OBP(AAS)
∴ PA=PB(全等三角形对应边相等)
∵ PA⊥OA于A,PB⊥OB于B
∴∠OAP=∠OBP=90°
∠ OAP= ∠ OBP(已证)
OP=OP(公共边)
探
究
结
果
角的平分线上的点到角的两边的距离相等.
角平分线的性质
PD ⊥OA于D ,
PE ⊥OB于E
∵OP平分∠AOB
∴PD=PE.
几何语言:
一平分 两垂直 得相等
(角的平分线上的点到这个角的两边的距离相等)
A
O
B
P
E
D
角平分线有什么性质?
猜一猜
角平分线线上的点到角的两边的距离相等。
通过动手实验、观察比较,我们发现“角的平分线上的点到角的两边的距离相等”,你能通过严格的逻辑推理证明这个结论吗?
已知:∠AOC = ∠BOC,点P在OC上,
PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD =PE.
A
B
O
P
C
D
E
证一证
已知:∠AOC= ∠BOC ,点P在OC上,PD⊥OA于D,
PE⊥OB于E.
求证: PD=PE.
O
A
B
E
D
P
C
∵ PD⊥OA,PE⊥OB
证明:
∴ ∠PDO= ∠PEO= 90°
在△POD 和 △PEO 中
∴ △PDO ≌△PEO(AAS)
∠ PDO=∠PEO
∠ AOC=∠BOC
OP=OP
∴ PD=PE
由角的平分线的性质的证明过程,你能概
括出证明几何命题的一般步骤吗?
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用数学符号
表示已知和求证;
(3)经过分析,找出由已知推出求证的途
径,写出证明过程.
归纳
角的平分线的性质的作用是什么?
主要是用于判断和证明两条线段相等,与以
前的方法相比,运用此性质不需要先证两个三角
形全等.
思考
例题学习
例 如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F.
∴PD=PE.
同理PE=PF.
∴PD=PE=PF
即点P到三边AB、BC、CA的距离相等.
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1︰20000)
解决问题
S
公路
铁路
已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
◆证明: ∵AD平分∠CAB
DE⊥AB ,DF⊥AC(已知)
∴DE=DF (角平分线的性质)
在Rt△BED和Rt△CFD中,
BD=CD (已证)
DE=DF (已知)
∴ Rt△ BED ≌Rt△CFD (HL)
∴ BE=FC (全等三角形对应边相等)
回味无穷
性质 角平分线上的点到这个角的两边距离相等.
几何语言:
∵OC是∠AOB的平分线,
P是OC上任意一点 PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
课堂 小结
P
A
O
B
C
E
D
1
2
