2022—2023学年人教版数学七年级上册2.2.2 整式的加减--去括号课件 (共18张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册2.2.2 整式的加减--去括号课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 780.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 12:16:55 | ||
图片预览


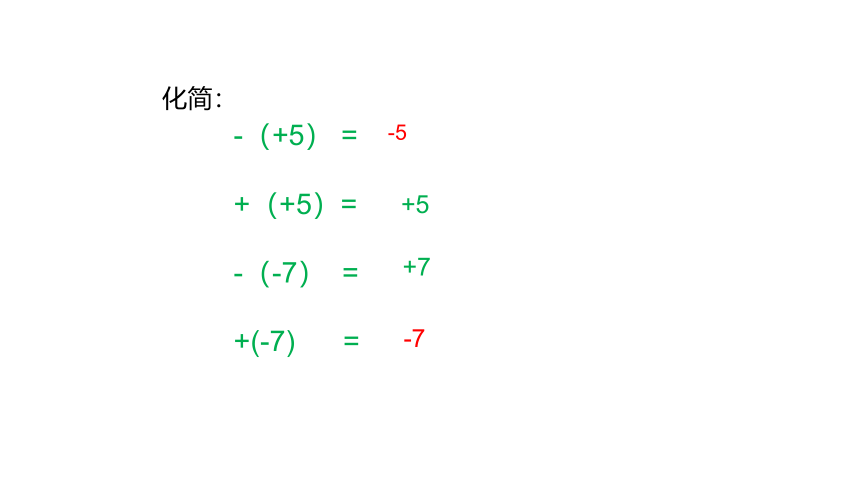

文档简介
(共18张PPT)
2.2 整式的加减第2课时(去括号)
知识讲解
96÷ 12+4 ×2
1
2
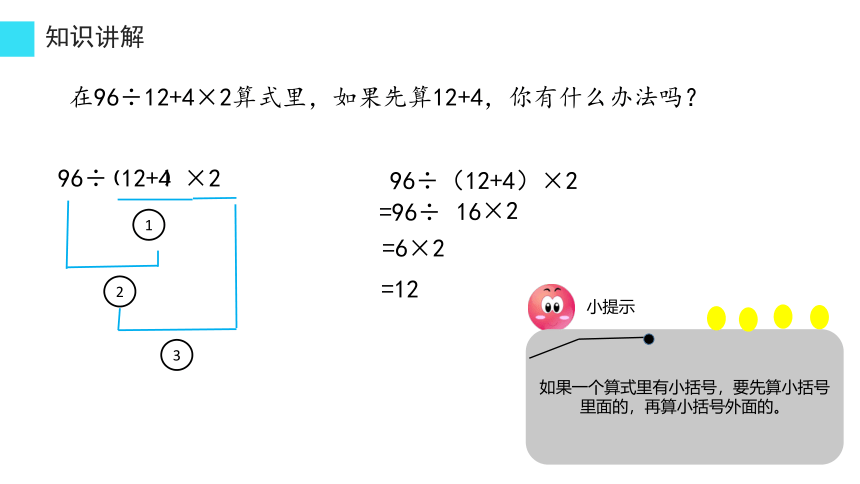
在96÷12+4×2算式里,如果先算12+4,你有什么办法吗?
3
96÷(12+4)×2
=96÷
16
×2
=6×2
=12
如果一个算式里有小括号,要先算小括号里面的,再算小括号外面的。
小提示
( )
知识讲解
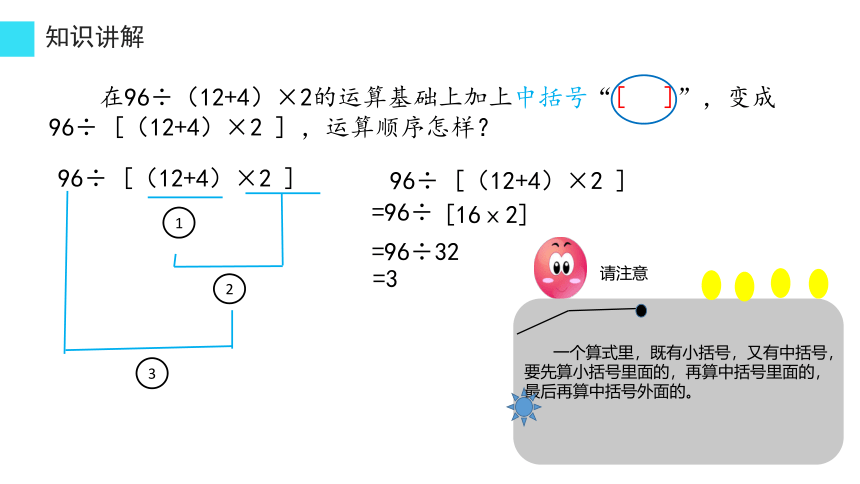
在96÷(12+4)×2的运算基础上加上中括号“[ ]”,变成
96÷ [(12+4)×2 ] ,运算顺序怎样?
96÷ [(12+4)×2 ]
1
2
3
96÷ [(12+4)×2 ]
=96÷
[16ⅹ2]
=96÷32
=3
一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后再算中括号外面的。
请注意
96÷12+4×2
96÷(12+4)×2
1
2
3
96÷ [(12+4)×2 ]
1
2
3
1
2
3
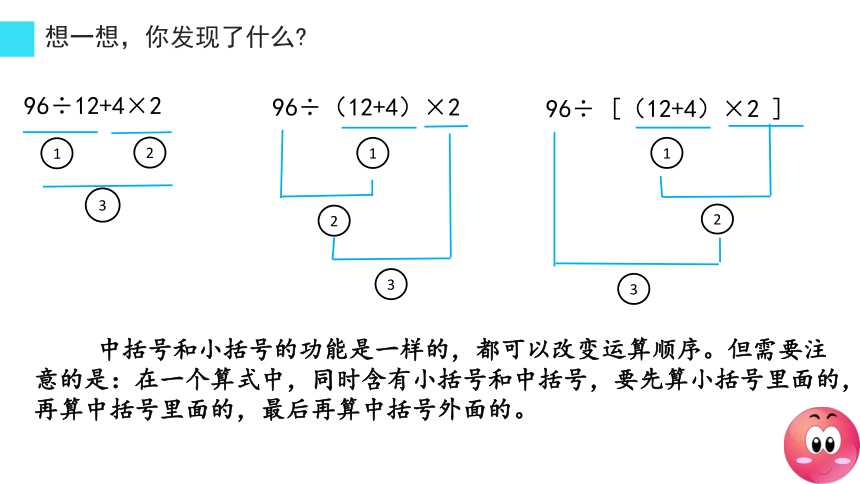
想一想,你发现了什么
中括号和小括号的功能是一样的,都可以改变运算顺序。但需要注
意的是:在一个算式中,同时含有小括号和中括号,要先算小括号里面的,
再算中括号里面的,最后再算中括号外面的。
你知道吗?
小括号“( )”是公元17世纪由荷兰人吉拉特首先使用的。
中括号“ [ ]”是公元17世纪英国数学家瓦里士最先使用的。
在以后的学习中,还会用到大括号“{ }”,又称为花括号。大括号是法国数学家韦达在1593年首先使用的。
化简:
你能指出它们的共同特点吗?
-(+5) =
+(+5)=
-(-7) =
+(-7) =
-5
+5
+7
-7
想一想:
根据分配律,你能为下面的式子去括号吗?
(1) +(-a+c) (2) -(-a-c)
解:原式=+1× (-a+c)
=1× (-a)+1 × c
=-a+c
解:原式=(-1)×(-a-c)
=(-1) × (-a)+(-1)×(-c)
=a+c
表示-a和-c的和,即-a+(-c)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
+(-a+c)=-a+c
-(-a-c)=a+c
符号不变
符号相反
符号不变
符号相反
去括号法则:
简记为:去括号,看符号
是“+”号,不变号
是“-”号,全变号
分析
如果括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项符号都不变;
如果括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项符号都改变;
直观理解:
去掉“+()”,括号内各项的符号不变
去掉“-()”,括号内各项的符号改变
a+(b+c)= a+b+c
a-(b+c) = a-b-c
用三个字母a,b,c表示去括号前后的变化规律:
例:化简(5a-3b)-3(-a2+2b)
举一反三
表示-a2与+2b的和
即-a2+(+2b)
解:原式=5a-3b
+3a2
-6b
=3a2+5a-9b
游戏:
(1)a+(b-c) (5)a-b+c
(2)a-(b-c) (6)-a-b+c
(3)-a+(-b+c) (7)-a+b-c
(4)-a-( -b+c ) (8)a+b-c
你能找到它们的好朋友吗?
趁热打铁
1、填空:
(1). -(m-n)= _____________________.
(2). -(a-b)+3(a-b)=_____________________.
(3). -[-(m-n)]= _____________________ .
(4). y-2(x-y)= _____________________ .
跟踪练习
(1).4a+(-a+3)=4a+a+3
(2).(2a-b)-(6b-7a)=2a-b-6b-7a
(3).3(x-2y)-2(4x-6y)=3x-6y-8x+6y
(4).-(2x+4y)+(6x-2y+1)=-2x-4y+6x-2y
2、判断
跟踪练习
3.计算:
(1) 8a+2b+(5a-b)
(2) (5a-3b)-3(a2-2b)
(3) - (x3-2x2-4)-(2x3-4);
跟踪练习
4.一个多项式加-x2+x+2得x2-1,则这个多项式为_________.
跟踪练习
5.有理数a,b,c在数轴上的位置如图所示,化简代数式
3|a-b|+|a+b|-|c-a|+2|b-c|.
1.去括号法则。
2.去括号应注意的问题。
课堂小结
当堂达标
1.化简;
① a+2(–b+c) = ②(a–b)–(c+d)=
③–(–a+b)–c= ④ 2x–3(x2–y2) =
2.去括号并合并;
① m-n-(m+n)= .
② a-(b-c)+(b-a)= .
3 .化简-2a-5a-[2a-(2a-3)+(2-3a)]的结果是_________.
2.2 整式的加减第2课时(去括号)
知识讲解
96÷ 12+4 ×2
1
2
在96÷12+4×2算式里,如果先算12+4,你有什么办法吗?
3
96÷(12+4)×2
=96÷
16
×2
=6×2
=12
如果一个算式里有小括号,要先算小括号里面的,再算小括号外面的。
小提示
( )
知识讲解
在96÷(12+4)×2的运算基础上加上中括号“[ ]”,变成
96÷ [(12+4)×2 ] ,运算顺序怎样?
96÷ [(12+4)×2 ]
1
2
3
96÷ [(12+4)×2 ]
=96÷
[16ⅹ2]
=96÷32
=3
一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后再算中括号外面的。
请注意
96÷12+4×2
96÷(12+4)×2
1
2
3
96÷ [(12+4)×2 ]
1
2
3
1
2
3
想一想,你发现了什么
中括号和小括号的功能是一样的,都可以改变运算顺序。但需要注
意的是:在一个算式中,同时含有小括号和中括号,要先算小括号里面的,
再算中括号里面的,最后再算中括号外面的。
你知道吗?
小括号“( )”是公元17世纪由荷兰人吉拉特首先使用的。
中括号“ [ ]”是公元17世纪英国数学家瓦里士最先使用的。
在以后的学习中,还会用到大括号“{ }”,又称为花括号。大括号是法国数学家韦达在1593年首先使用的。
化简:
你能指出它们的共同特点吗?
-(+5) =
+(+5)=
-(-7) =
+(-7) =
-5
+5
+7
-7
想一想:
根据分配律,你能为下面的式子去括号吗?
(1) +(-a+c) (2) -(-a-c)
解:原式=+1× (-a+c)
=1× (-a)+1 × c
=-a+c
解:原式=(-1)×(-a-c)
=(-1) × (-a)+(-1)×(-c)
=a+c
表示-a和-c的和,即-a+(-c)
观察这两组算式,看看去括号前后,括号里各项的符号有什么变化?
+(-a+c)=-a+c
-(-a-c)=a+c
符号不变
符号相反
符号不变
符号相反
去括号法则:
简记为:去括号,看符号
是“+”号,不变号
是“-”号,全变号
分析
如果括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项符号都不变;
如果括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项符号都改变;
直观理解:
去掉“+()”,括号内各项的符号不变
去掉“-()”,括号内各项的符号改变
a+(b+c)= a+b+c
a-(b+c) = a-b-c
用三个字母a,b,c表示去括号前后的变化规律:
例:化简(5a-3b)-3(-a2+2b)
举一反三
表示-a2与+2b的和
即-a2+(+2b)
解:原式=5a-3b
+3a2
-6b
=3a2+5a-9b
游戏:
(1)a+(b-c) (5)a-b+c
(2)a-(b-c) (6)-a-b+c
(3)-a+(-b+c) (7)-a+b-c
(4)-a-( -b+c ) (8)a+b-c
你能找到它们的好朋友吗?
趁热打铁
1、填空:
(1). -(m-n)= _____________________.
(2). -(a-b)+3(a-b)=_____________________.
(3). -[-(m-n)]= _____________________ .
(4). y-2(x-y)= _____________________ .
跟踪练习
(1).4a+(-a+3)=4a+a+3
(2).(2a-b)-(6b-7a)=2a-b-6b-7a
(3).3(x-2y)-2(4x-6y)=3x-6y-8x+6y
(4).-(2x+4y)+(6x-2y+1)=-2x-4y+6x-2y
2、判断
跟踪练习
3.计算:
(1) 8a+2b+(5a-b)
(2) (5a-3b)-3(a2-2b)
(3) - (x3-2x2-4)-(2x3-4);
跟踪练习
4.一个多项式加-x2+x+2得x2-1,则这个多项式为_________.
跟踪练习
5.有理数a,b,c在数轴上的位置如图所示,化简代数式
3|a-b|+|a+b|-|c-a|+2|b-c|.
1.去括号法则。
2.去括号应注意的问题。
课堂小结
当堂达标
1.化简;
① a+2(–b+c) = ②(a–b)–(c+d)=
③–(–a+b)–c= ④ 2x–3(x2–y2) =
2.去括号并合并;
① m-n-(m+n)= .
② a-(b-c)+(b-a)= .
3 .化简-2a-5a-[2a-(2a-3)+(2-3a)]的结果是_________.
