人教版数学七年级上册2.1.3 多项式及整式 课时练习 (word版含答案)
文档属性
| 名称 | 人教版数学七年级上册2.1.3 多项式及整式 课时练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 10:32:09 | ||
图片预览



文档简介
第3课时 多项式及整式
(
基础知识精炼
模块一
)
(
【
知识点
1
】多项式及其相关概念
)
1.多项式﹣3a3b+xy﹣1的次数是( )
A.3 B.4 C.6 D.7
2.多项式a3b4﹣2a2b4+3的项数和次数分别是( )
A.2,6 B.3,6 C.2,7 D.3,7
3.对于多项式2x3+3x2﹣1,下列说法中错误的是( )
A.多项式的次数是3 B.二次项系数为3
C.一次项系数为0 D.常数项为1
4.下列说法正确的是( )
A.的系数是 B.x3y+x2﹣1是三次三项式
C.x2﹣2x﹣1的常数项是1 D.是多项式
(
【
知识点
2
】整式的概念
)
5.下列各式中,不是整式的是( )
A.3a B. C.0 D.x+y
6.在式子,x+y+1,2021,﹣a,﹣3x2y,中,整式的个数( )
A.6个 B.5个 C.4个 D.3个
7.请写出一个只含有字母x,y,且次数不超过2的整式: .
(
【
知识点
3
】实际问题中的多项式
)
8.为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.8x元 B.10(100﹣x)元
C.8(100﹣x)元 D.(100﹣8x)元
9.某企业去年的年产值为42亿元,预计今年比去年增长x,假设明年的增长率与今年相同,则明年的年产值可表示为( )亿元
A.84x B.42(1+2x) C.42(1+x)2 D.42(1+x)
10.边长分别为a和b(其中a>b)的两个正方形按如图摆放,则图中阴影部分的面积为( )
A. B.2ab C.a2+ab D.
11.某种桔子的售价是每千克3元,用面值为100元的人民币购买了a千克,应找回 元.
(
综合能力提升
模块二
)
12.将多项式﹣9+x3+3xy2﹣x2y按x的降幂排列的结果为( )
A.x3+x2y﹣3xy2﹣9 B.﹣9+3xy2﹣x2y+x3
C.﹣9﹣3xy2+x2y+x3 D.x3﹣x2y+3xy2﹣9
13.下列说法中,正确的个数( )
①单项式与多项式统称为整式;②单项式x2yz的系数是1;③xy+x+3是二次三项式;④x的次数是0;⑤5a2b,3ab,7是多项式5a2b+3ab﹣7的项.
A.1 B.2 C.3 D.4
14.下列代数式中,既不是单项式,也不是多项式的是( )
A. B.xy C.2x2+1 D.
15.如果2x3ym+(n﹣2)x是关于x,y的五次二项式,则关于m,n的值描述正确的是( )
A.m=3,n≠2 B.m=2,n=3 C.m=3,n=2 D.m=2,n≠2
16.下列各式mn,8,,x2+2x+6,,,﹣a中,整式有( )
A.4个 B.5个 C.6个 D.7个
17.长为acm,宽为bcm(a>b>5)的长方形,若将长增加5cm,宽减少5cm,则它的面积会( )
A.变小 B.变大 C.不变 D.无法确定
18.某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )
A.先提价50%,再打六折
B.先打九五折,再打九五折
C.先提价30%,再降价30%
D.先提价25%,再降价25%
19.已知多项式﹣3x3ym+1+xy2x3+6是六次四项式,单项式πxny5﹣m的次数与这个多项式的次数相同,求mn的值.
20.把下列代数式的序号填入相应的横线上:
①a2b+ab2+b3②③④⑤0⑥﹣x⑦⑧3x2⑨⑩
(1)单项式
(2)多项式
(3)整式
(4)二项式 .
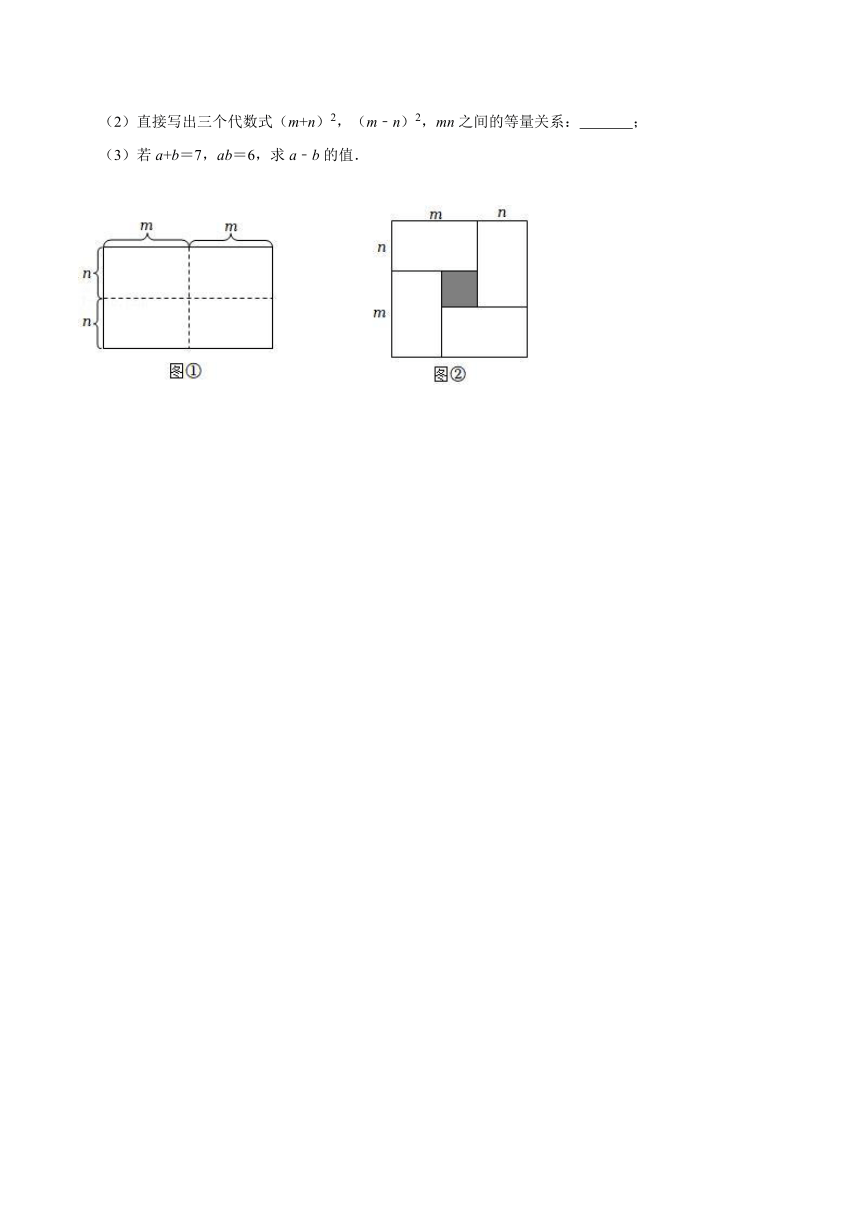
21.图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它平均分成形状和大小都一样的四块小长方形,然后按图②那样拼成一个正方形.
(1)观察图②,请用两种不同的方法表示图②中阴影部分的面积:
方法1: ;
方法2: ;
(2)直接写出三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系: ;
(3)若a+b=7,ab=6,求a﹣b的值.
参考答案
1.解:多项式3a3b+xy﹣1的次数是4,
故选:B.
2.解:∵多项式a3b4﹣2a2b4+3共有3项,次数最高的项是:a3b4,其次数为:3+4=7,
∴该多项式的次数为7.
故选:D.
3.解:A、多项式的次数是3,正确,不符合题意;
B、二次项系数为3正确,不符合题意;
C、一次项系数为0,正确,不符合题意;
D、常数项为﹣1,故本选项错误,符合题意;
故选:D.
4.解:A.根据单项式系数的定义,得的系数为,那么A不符合题意.
B.根据多项式的次数以及项数的定义,得x3y+x2﹣1的次数为4,项数为3,即多项式x3y+x2﹣1为四次三项式,那么B不符合题意.
C.x2﹣2x﹣1的常数项是﹣1,那么C不符合题意.
D.根据多项式的定义,含、这两项,是多项式.
故选:D.
5.解:A、3a是整式,不符合题意;
B、是分式,不是整式,符合题意;
C、0是整式,不符合题意;
D、x+y是整式,不符合题意;
故选:B.
6.解:在式子,x+y+1,2021,﹣a,﹣3x2y,中,整式是:x+y+1,2021,﹣a,﹣3x2y,,
共有5个,
故选:B.
7.解:只含有字母x,y,且次数不超过2的整式:答案不唯一,如3xy,x+y,x2+2xy+y2….
故答案为:答案不唯一,如3xy,x+y,x2+2xy+y2….
8.解:设购买甲种读本x本,则购买乙种读本的费用为:8(100﹣x)元.
故选:C.
9.解:明年的年产值为:42(1+x)2亿元.
故选:C.
10.解:∵大正方形的边长为a,小正方形的边长为b,
∴大正方形的面积为a2,小正方形的面积为b2,
∴阴影部分的面积为:a2+b2a(a+b)b(a﹣b),
故选:A.
11.解:根据题意,a千克桔子售价为3a元,所以应找回(100﹣3a)元.
故答案为:(100﹣3a).
12.解:﹣9+x3+3xy2﹣x2y按x的降幂排列为:x3﹣x2y+3xy2﹣9,
故选:D.
13.解:①整式的概念:单项式和多项式统称为整式.故本选项符合题意.
②单项式x2yz的系数是1.故本选项符合题意.
③xy+x+3是二次三项式.故本选项符合题意.
④x的次数是1.故本选项不符合题意.
⑤5a2b,3ab,﹣7是多项式5a2b+3ab﹣7的项,故本选项不符合题意.
故正确的个数有3个正确的个数.
故选:C.
14.解:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数.
数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.
所以不是单项式也不是多项式,
故选:A.
15.解:∵2x3ym+(n﹣2)x是关于x,y的五次二项式,
∴3+m=5,n﹣2≠0,
∴m=2,n≠2;
故选:D.
16.解:和的分母含有字母,是分式,不是整式;
整式有mn,8,x2+2x+6,,﹣a,共有5个,
故选:B.
17.解:原长方形的面积为:abcm2,
现长方形的面积为:(a+5)(b﹣5)=(ab+5b﹣5a﹣25)cm2,
因为b<a,
所以b﹣a<0,
所以ab+5b﹣5a﹣25﹣ab=5(b﹣a)﹣25<0,
即现长方形的面积小于原长方形的面积.
故选:A.
18.解:A、先提价50%,再打六折的售价为:(1+50%)×0.6a=0.9a(元);
B、先打九五折,再打九五折的售价为:0.95×0.95a=0.9025a(元);
C、先提价30%,再降价30%的售价为:(1+30%)(1﹣30%)a=0.91a(元);
D、先提价25%,再降价25%的售价为:(1+25%)(1﹣25%)a=0.9375a(元);
∵0.9a<0.9025a<0.91a<0.9375a,
∴A选项的调价方案调价后售价最低,
故选:A.
19.解:由题意可知:m+1+3=6,n+5﹣m=6,
∴m=2,n=3,
∴mn=23=8
20.解:(1)单项式 ④⑤⑩
(2)多项式 ①③⑥
(3)整式 ①③④⑤⑥⑩
(4)二项式 ③⑥.
故答案为:(1)④⑤⑩;(2)①③⑥;(3)①③④⑤⑥⑩;(4)③⑥.
21.解:(1)方法1:(m﹣n)2;方法2:(m+n)2﹣4mn.
故答案为:(m﹣n)2;(m+n)2﹣4mn;
(2)(m+n)2,(m﹣n)2,mn之间的等量关系:(m﹣n)2=(m+n)2﹣4mn.
故答案为:(m﹣n)2=(m+n)2﹣4mn;
(3)∵a+b=7,ab=6,
∴(a﹣b)2=(a+b)2﹣4ab=49﹣24=25,
∴a﹣b=±5.
(
基础知识精炼
模块一
)
(
【
知识点
1
】多项式及其相关概念
)
1.多项式﹣3a3b+xy﹣1的次数是( )
A.3 B.4 C.6 D.7
2.多项式a3b4﹣2a2b4+3的项数和次数分别是( )
A.2,6 B.3,6 C.2,7 D.3,7
3.对于多项式2x3+3x2﹣1,下列说法中错误的是( )
A.多项式的次数是3 B.二次项系数为3
C.一次项系数为0 D.常数项为1
4.下列说法正确的是( )
A.的系数是 B.x3y+x2﹣1是三次三项式
C.x2﹣2x﹣1的常数项是1 D.是多项式
(
【
知识点
2
】整式的概念
)
5.下列各式中,不是整式的是( )
A.3a B. C.0 D.x+y
6.在式子,x+y+1,2021,﹣a,﹣3x2y,中,整式的个数( )
A.6个 B.5个 C.4个 D.3个
7.请写出一个只含有字母x,y,且次数不超过2的整式: .
(
【
知识点
3
】实际问题中的多项式
)
8.为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x本,则购买乙种读本的费用为( )
A.8x元 B.10(100﹣x)元
C.8(100﹣x)元 D.(100﹣8x)元
9.某企业去年的年产值为42亿元,预计今年比去年增长x,假设明年的增长率与今年相同,则明年的年产值可表示为( )亿元
A.84x B.42(1+2x) C.42(1+x)2 D.42(1+x)
10.边长分别为a和b(其中a>b)的两个正方形按如图摆放,则图中阴影部分的面积为( )
A. B.2ab C.a2+ab D.
11.某种桔子的售价是每千克3元,用面值为100元的人民币购买了a千克,应找回 元.
(
综合能力提升
模块二
)
12.将多项式﹣9+x3+3xy2﹣x2y按x的降幂排列的结果为( )
A.x3+x2y﹣3xy2﹣9 B.﹣9+3xy2﹣x2y+x3
C.﹣9﹣3xy2+x2y+x3 D.x3﹣x2y+3xy2﹣9
13.下列说法中,正确的个数( )
①单项式与多项式统称为整式;②单项式x2yz的系数是1;③xy+x+3是二次三项式;④x的次数是0;⑤5a2b,3ab,7是多项式5a2b+3ab﹣7的项.
A.1 B.2 C.3 D.4
14.下列代数式中,既不是单项式,也不是多项式的是( )
A. B.xy C.2x2+1 D.
15.如果2x3ym+(n﹣2)x是关于x,y的五次二项式,则关于m,n的值描述正确的是( )
A.m=3,n≠2 B.m=2,n=3 C.m=3,n=2 D.m=2,n≠2
16.下列各式mn,8,,x2+2x+6,,,﹣a中,整式有( )
A.4个 B.5个 C.6个 D.7个
17.长为acm,宽为bcm(a>b>5)的长方形,若将长增加5cm,宽减少5cm,则它的面积会( )
A.变小 B.变大 C.不变 D.无法确定
18.某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )
A.先提价50%,再打六折
B.先打九五折,再打九五折
C.先提价30%,再降价30%
D.先提价25%,再降价25%
19.已知多项式﹣3x3ym+1+xy2x3+6是六次四项式,单项式πxny5﹣m的次数与这个多项式的次数相同,求mn的值.
20.把下列代数式的序号填入相应的横线上:
①a2b+ab2+b3②③④⑤0⑥﹣x⑦⑧3x2⑨⑩
(1)单项式
(2)多项式
(3)整式
(4)二项式 .
21.图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它平均分成形状和大小都一样的四块小长方形,然后按图②那样拼成一个正方形.
(1)观察图②,请用两种不同的方法表示图②中阴影部分的面积:
方法1: ;
方法2: ;
(2)直接写出三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系: ;
(3)若a+b=7,ab=6,求a﹣b的值.
参考答案
1.解:多项式3a3b+xy﹣1的次数是4,
故选:B.
2.解:∵多项式a3b4﹣2a2b4+3共有3项,次数最高的项是:a3b4,其次数为:3+4=7,
∴该多项式的次数为7.
故选:D.
3.解:A、多项式的次数是3,正确,不符合题意;
B、二次项系数为3正确,不符合题意;
C、一次项系数为0,正确,不符合题意;
D、常数项为﹣1,故本选项错误,符合题意;
故选:D.
4.解:A.根据单项式系数的定义,得的系数为,那么A不符合题意.
B.根据多项式的次数以及项数的定义,得x3y+x2﹣1的次数为4,项数为3,即多项式x3y+x2﹣1为四次三项式,那么B不符合题意.
C.x2﹣2x﹣1的常数项是﹣1,那么C不符合题意.
D.根据多项式的定义,含、这两项,是多项式.
故选:D.
5.解:A、3a是整式,不符合题意;
B、是分式,不是整式,符合题意;
C、0是整式,不符合题意;
D、x+y是整式,不符合题意;
故选:B.
6.解:在式子,x+y+1,2021,﹣a,﹣3x2y,中,整式是:x+y+1,2021,﹣a,﹣3x2y,,
共有5个,
故选:B.
7.解:只含有字母x,y,且次数不超过2的整式:答案不唯一,如3xy,x+y,x2+2xy+y2….
故答案为:答案不唯一,如3xy,x+y,x2+2xy+y2….
8.解:设购买甲种读本x本,则购买乙种读本的费用为:8(100﹣x)元.
故选:C.
9.解:明年的年产值为:42(1+x)2亿元.
故选:C.
10.解:∵大正方形的边长为a,小正方形的边长为b,
∴大正方形的面积为a2,小正方形的面积为b2,
∴阴影部分的面积为:a2+b2a(a+b)b(a﹣b),
故选:A.
11.解:根据题意,a千克桔子售价为3a元,所以应找回(100﹣3a)元.
故答案为:(100﹣3a).
12.解:﹣9+x3+3xy2﹣x2y按x的降幂排列为:x3﹣x2y+3xy2﹣9,
故选:D.
13.解:①整式的概念:单项式和多项式统称为整式.故本选项符合题意.
②单项式x2yz的系数是1.故本选项符合题意.
③xy+x+3是二次三项式.故本选项符合题意.
④x的次数是1.故本选项不符合题意.
⑤5a2b,3ab,﹣7是多项式5a2b+3ab﹣7的项,故本选项不符合题意.
故正确的个数有3个正确的个数.
故选:C.
14.解:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数.
数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.
所以不是单项式也不是多项式,
故选:A.
15.解:∵2x3ym+(n﹣2)x是关于x,y的五次二项式,
∴3+m=5,n﹣2≠0,
∴m=2,n≠2;
故选:D.
16.解:和的分母含有字母,是分式,不是整式;
整式有mn,8,x2+2x+6,,﹣a,共有5个,
故选:B.
17.解:原长方形的面积为:abcm2,
现长方形的面积为:(a+5)(b﹣5)=(ab+5b﹣5a﹣25)cm2,
因为b<a,
所以b﹣a<0,
所以ab+5b﹣5a﹣25﹣ab=5(b﹣a)﹣25<0,
即现长方形的面积小于原长方形的面积.
故选:A.
18.解:A、先提价50%,再打六折的售价为:(1+50%)×0.6a=0.9a(元);
B、先打九五折,再打九五折的售价为:0.95×0.95a=0.9025a(元);
C、先提价30%,再降价30%的售价为:(1+30%)(1﹣30%)a=0.91a(元);
D、先提价25%,再降价25%的售价为:(1+25%)(1﹣25%)a=0.9375a(元);
∵0.9a<0.9025a<0.91a<0.9375a,
∴A选项的调价方案调价后售价最低,
故选:A.
19.解:由题意可知:m+1+3=6,n+5﹣m=6,
∴m=2,n=3,
∴mn=23=8
20.解:(1)单项式 ④⑤⑩
(2)多项式 ①③⑥
(3)整式 ①③④⑤⑥⑩
(4)二项式 ③⑥.
故答案为:(1)④⑤⑩;(2)①③⑥;(3)①③④⑤⑥⑩;(4)③⑥.
21.解:(1)方法1:(m﹣n)2;方法2:(m+n)2﹣4mn.
故答案为:(m﹣n)2;(m+n)2﹣4mn;
(2)(m+n)2,(m﹣n)2,mn之间的等量关系:(m﹣n)2=(m+n)2﹣4mn.
故答案为:(m﹣n)2=(m+n)2﹣4mn;
(3)∵a+b=7,ab=6,
∴(a﹣b)2=(a+b)2﹣4ab=49﹣24=25,
∴a﹣b=±5.
