(2022秋季新教材)人教版六年级数学上册5.3.4 练习十五 课件(共23张PPT)
文档属性
| 名称 | (2022秋季新教材)人教版六年级数学上册5.3.4 练习十五 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 20:41:13 | ||
图片预览






文档简介
(共23张PPT)
2022秋 人教数学
六年级上册
练习十五
圆
5
圆的直径与半径的关系:
圆的面积计算的公式:
d=2r
S=πr
圆的周长计算的公式:
C=2πr
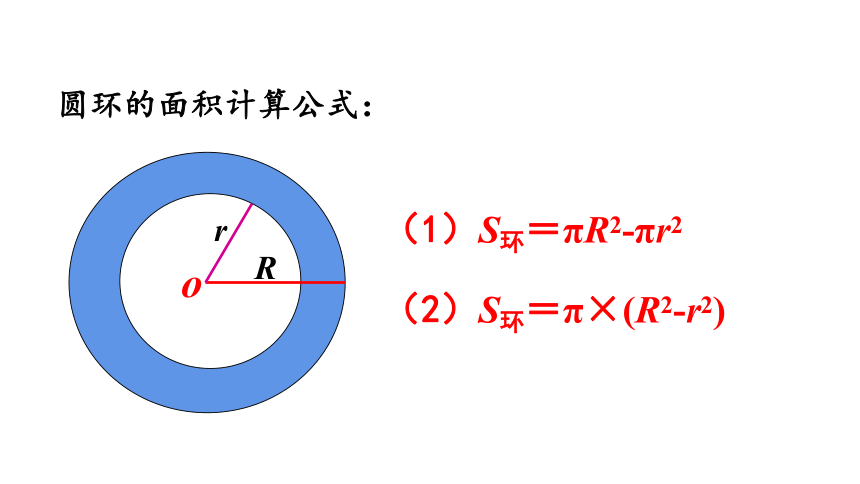
(1)S环=πR2-πr2
(2)S环=π×(R2-r2)
R
r
圆环的面积计算公式:
o
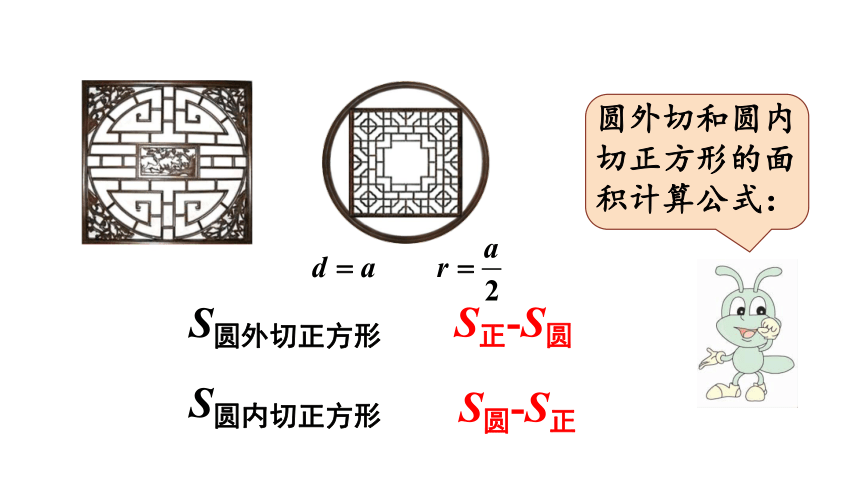
S正-S圆
S圆-S正
S圆外切正方形
S圆内切正方形
圆外切和圆内切正方形的面积计算公式:
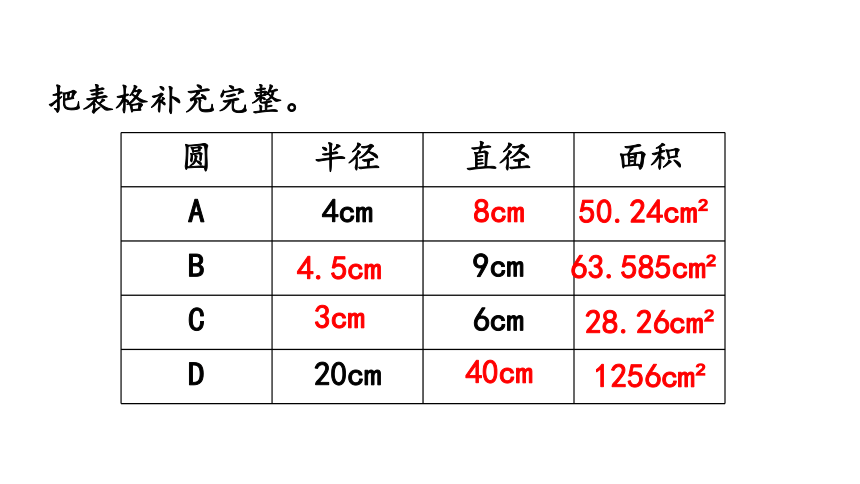
圆 半径 直径 面积
A 4cm
B 9cm
C 6cm
D 20cm
把表格补充完整。
8cm
3cm
4.5cm
40cm
50.24cm
63.585cm
28.26cm
1256cm
计算下面各圆的周长和面积。
d = 10 cm
C = 3.14×10
= 31.4(cm)
S = 3.14×(10÷2)2
= 78.5(cm2)
r = 3 cm
S = 3.14×32
= 28.26(cm2)
C = 2×3.14×3
= 18.84(cm)
计算下面各圆的周长和面积。
公园草地上一个自动旋转喷灌装置的射程是10m,它能喷灌的面积是多少?
S = πr2
= 3.14×102
= 3.14×100
= 314(m2)
答:它能喷灌的面积是314m2。
小刚量得一棵树的树干横截面的周长是125.6 cm。树干的横截面近似于圆,它的面积大约是多少?
r = 125.6÷3.14÷2
= 20(cm)
C = 2πr
S = πr2
= 3.14×202
= 3.14×400
= 1256(cm2)
答:它的面积大约是1256cm2。
右图是一块玉壁,外直径为18cm,
内直径为7cm。这块玉壁的面积是多少?
3.14×(92 - 3.52)
= 3.14×68.75
= 215.875(cm )
外半径:18÷2
内半径:7÷2
= 9(cm)
= 3.5(cm)
答:这块玉壁的面积是215.875cm2。
= 3.14×(81 - 12.25)
图中的大圆半径等于小圆的直径,请你求出涂色部分的面积。
6 cm
小圆半径:6÷2
= 3(cm)
3.14×(62 - 32)
= 3.14×27
= 84.78(cm )
答:涂色部分的面积是84.78cm2。
= 3.14×(36 - 9)
计算下面图形的周长。
8cm
12cm
大半圆弧 + 小半圆弧 + 2条线段
C大半圆弧 = πd÷2
= 3.14×12÷2
= 18.84(cm)
C小半圆弧 = πd÷2
= 3.14×8÷2
= 12.56(cm)
18.84 + 12.56 + 4
= 35.4(cm)
两条线段长度:12 - 8
= 4(cm)
答:图形的周长是35.4cm。
.
计算下面圆环的面积。
12cm
8cm
3.14×(122 - 82)
= 3.14×80
= 251.2(cm )
答:圆环的面积是251.2cm2。
= 3.14×(144 - 64)
右图中的铜钱直径为28mm,中间正方形的边长为6mm。
这枚铜钱的面积是多少?
3.14×142 - 62
= 615.44 - 36
= 579.44(mm )
答:这枚铜钱的面积是579.44mm2。
= 3.14×196 - 36
r = 28÷2
= 14(mm)
如右图,一个运动场两端是半圆形,中间是长方形。这个
运动场的周长是多少米?面积是多少平方米?
100m
32m
O
C = 2×3.14×32 + 100×2
= 200.96 + 200
= 400.9(m)
S = 3.14×322 + 100×(32×2)
= 3.14×322 + 100×64
= 3215.36 + 6400
= 9615.36(m2)
答:这个运动场的周长是400.9m,面积是9615.36m2。
右图中的花瓣状门洞的边是由4个直径都是1m的半圆组成的。
这个门洞的周长和面积分别是多少?
= 2×3.14×1
= 6.28(m)
C = 2C圆
S = 2S圆 + S正方形
= 2×3.14×(1÷2)2 + 12
= 2×3.14×0.25 + 1
= 1.57 + 1
= 2.57(m2)
答:这个门洞的周长是6.28m,面积是2.57m2。
高致病性的禽流感是比非典病毒传染速度更快的传染病。为了防止禽流感的蔓延,政府规定:离疫点3千米的范围内为疫区,所有的禽类全部捕杀深埋;离疫点3千米至5千米范围内为免疫区,所有的禽类强制免疫,同时对疫区和免疫区内的村庄,实行道路全封闭管理。
A .
请你在图中分别画出疫区和免疫区的范围,并求出疫区和免疫区之间的面积是多少平方千米?
3.14×(52-32)=50.24(平方千米)
疫区
免疫区
答:疫区和免疫区之间的面积是50.24平方千米。
土楼是福建、广东等地的一种居民建筑,外围形状有圆形、方形、椭圆形等。有两座底面是圆环形的土楼,其中一座外直径34 m,内直径14 m;另一座外直径26 m,内直径也是14 m;两座土楼的房屋占地面积相差多少?
r1外 = 34÷2
r1内 = r2内 = 14÷2
r2外 = 26÷2
= 17(m)
= 7(m)
= 13(m)
3.14×(172 - 72)- 3.14×(132 - 72)
= 3.14×120
= 376.8(m )
= 3.14×(172 - 72 - 132 + 72)
= 3.14×(172 - 132)
答:两座土楼的房屋占地面积相差376.8m2。
一个圆的周长是62.8m,半径增加2m后,面积增加多少?
C = 2πr
r = C÷(2π)
= 62.8÷(2×3.14)
= 62.8÷6.28
= 10(m)
= π(r增加后2 - r2)
= 3.14×(144 - 100)
= 3.14×44
= 138.16(m2)
答:面积增加138.16m2。
r增加后 = 10 + 2
= 12(m)
= 3.14×(122 - 102)
S = S增加后 - S原来
如下图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?
一块半圆形草坪的周长等于整个圆周长的一半与2条半径的长度之和,即πr+2r=128.5 m。
先根据一块半圆形草坪的周长求出圆的半径,再利用圆的面积公式求出这两块草坪的总面积,即一个整圆的面积。
128.5÷(3.14+2)=25(m)
3.14×25 =1962.5(m )
答:这两块草坪的总面积是1962.5平方米。
如下图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?
这节课你们都学会了哪些知识?
要灵活运用圆的面积计算公式和圆环的面积计算公式解决实际问题。
2022秋 人教数学
六年级上册
练习十五
圆
5
圆的直径与半径的关系:
圆的面积计算的公式:
d=2r
S=πr
圆的周长计算的公式:
C=2πr
(1)S环=πR2-πr2
(2)S环=π×(R2-r2)
R
r
圆环的面积计算公式:
o
S正-S圆
S圆-S正
S圆外切正方形
S圆内切正方形
圆外切和圆内切正方形的面积计算公式:
圆 半径 直径 面积
A 4cm
B 9cm
C 6cm
D 20cm
把表格补充完整。
8cm
3cm
4.5cm
40cm
50.24cm
63.585cm
28.26cm
1256cm
计算下面各圆的周长和面积。
d = 10 cm
C = 3.14×10
= 31.4(cm)
S = 3.14×(10÷2)2
= 78.5(cm2)
r = 3 cm
S = 3.14×32
= 28.26(cm2)
C = 2×3.14×3
= 18.84(cm)
计算下面各圆的周长和面积。
公园草地上一个自动旋转喷灌装置的射程是10m,它能喷灌的面积是多少?
S = πr2
= 3.14×102
= 3.14×100
= 314(m2)
答:它能喷灌的面积是314m2。
小刚量得一棵树的树干横截面的周长是125.6 cm。树干的横截面近似于圆,它的面积大约是多少?
r = 125.6÷3.14÷2
= 20(cm)
C = 2πr
S = πr2
= 3.14×202
= 3.14×400
= 1256(cm2)
答:它的面积大约是1256cm2。
右图是一块玉壁,外直径为18cm,
内直径为7cm。这块玉壁的面积是多少?
3.14×(92 - 3.52)
= 3.14×68.75
= 215.875(cm )
外半径:18÷2
内半径:7÷2
= 9(cm)
= 3.5(cm)
答:这块玉壁的面积是215.875cm2。
= 3.14×(81 - 12.25)
图中的大圆半径等于小圆的直径,请你求出涂色部分的面积。
6 cm
小圆半径:6÷2
= 3(cm)
3.14×(62 - 32)
= 3.14×27
= 84.78(cm )
答:涂色部分的面积是84.78cm2。
= 3.14×(36 - 9)
计算下面图形的周长。
8cm
12cm
大半圆弧 + 小半圆弧 + 2条线段
C大半圆弧 = πd÷2
= 3.14×12÷2
= 18.84(cm)
C小半圆弧 = πd÷2
= 3.14×8÷2
= 12.56(cm)
18.84 + 12.56 + 4
= 35.4(cm)
两条线段长度:12 - 8
= 4(cm)
答:图形的周长是35.4cm。
.
计算下面圆环的面积。
12cm
8cm
3.14×(122 - 82)
= 3.14×80
= 251.2(cm )
答:圆环的面积是251.2cm2。
= 3.14×(144 - 64)
右图中的铜钱直径为28mm,中间正方形的边长为6mm。
这枚铜钱的面积是多少?
3.14×142 - 62
= 615.44 - 36
= 579.44(mm )
答:这枚铜钱的面积是579.44mm2。
= 3.14×196 - 36
r = 28÷2
= 14(mm)
如右图,一个运动场两端是半圆形,中间是长方形。这个
运动场的周长是多少米?面积是多少平方米?
100m
32m
O
C = 2×3.14×32 + 100×2
= 200.96 + 200
= 400.9(m)
S = 3.14×322 + 100×(32×2)
= 3.14×322 + 100×64
= 3215.36 + 6400
= 9615.36(m2)
答:这个运动场的周长是400.9m,面积是9615.36m2。
右图中的花瓣状门洞的边是由4个直径都是1m的半圆组成的。
这个门洞的周长和面积分别是多少?
= 2×3.14×1
= 6.28(m)
C = 2C圆
S = 2S圆 + S正方形
= 2×3.14×(1÷2)2 + 12
= 2×3.14×0.25 + 1
= 1.57 + 1
= 2.57(m2)
答:这个门洞的周长是6.28m,面积是2.57m2。
高致病性的禽流感是比非典病毒传染速度更快的传染病。为了防止禽流感的蔓延,政府规定:离疫点3千米的范围内为疫区,所有的禽类全部捕杀深埋;离疫点3千米至5千米范围内为免疫区,所有的禽类强制免疫,同时对疫区和免疫区内的村庄,实行道路全封闭管理。
A .
请你在图中分别画出疫区和免疫区的范围,并求出疫区和免疫区之间的面积是多少平方千米?
3.14×(52-32)=50.24(平方千米)
疫区
免疫区
答:疫区和免疫区之间的面积是50.24平方千米。
土楼是福建、广东等地的一种居民建筑,外围形状有圆形、方形、椭圆形等。有两座底面是圆环形的土楼,其中一座外直径34 m,内直径14 m;另一座外直径26 m,内直径也是14 m;两座土楼的房屋占地面积相差多少?
r1外 = 34÷2
r1内 = r2内 = 14÷2
r2外 = 26÷2
= 17(m)
= 7(m)
= 13(m)
3.14×(172 - 72)- 3.14×(132 - 72)
= 3.14×120
= 376.8(m )
= 3.14×(172 - 72 - 132 + 72)
= 3.14×(172 - 132)
答:两座土楼的房屋占地面积相差376.8m2。
一个圆的周长是62.8m,半径增加2m后,面积增加多少?
C = 2πr
r = C÷(2π)
= 62.8÷(2×3.14)
= 62.8÷6.28
= 10(m)
= π(r增加后2 - r2)
= 3.14×(144 - 100)
= 3.14×44
= 138.16(m2)
答:面积增加138.16m2。
r增加后 = 10 + 2
= 12(m)
= 3.14×(122 - 102)
S = S增加后 - S原来
如下图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?
一块半圆形草坪的周长等于整个圆周长的一半与2条半径的长度之和,即πr+2r=128.5 m。
先根据一块半圆形草坪的周长求出圆的半径,再利用圆的面积公式求出这两块草坪的总面积,即一个整圆的面积。
128.5÷(3.14+2)=25(m)
3.14×25 =1962.5(m )
答:这两块草坪的总面积是1962.5平方米。
如下图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?
这节课你们都学会了哪些知识?
要灵活运用圆的面积计算公式和圆环的面积计算公式解决实际问题。
