福建省福州第四十中学2022-2023学年八年级上学期开门考数学试卷(含解析)
文档属性
| 名称 | 福建省福州第四十中学2022-2023学年八年级上学期开门考数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 268.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 22:27:06 | ||
图片预览



文档简介
2022-2023学年福建省福州四十中八年级(上)开门考数学试卷
(附答案解析)
一、选择题(本大题共10小题,每小题4分,共40分。)
1.(4分)下列图形具有稳定性的是( )
A. B.
C. D.
2.(4分)下列计算结果正确的是( )
A.b b3=b4 B.a8÷a4=a2
C.4a3 2a2=8a6 D.(2a3)2=4a5
3.(4分)下列等式从左到右的变形是因式分解的是( )
A.2x(x+3)=2x2+6x B.x2﹣y2=(x+y)(x﹣y)
C.x2+2xy+y2+1=(x+y)2+1 D.24xy2=3x 8y2
4.(4分)如果等腰三角形的两边长分别3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15
5.(4分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
6.(4分)如图,在△ABC中,∠B=∠ACB=50°,P是边AB上的一个动点(不与顶点A重合),则∠BPC的度数可能是( )
A.50° B.80° C.100° D.130°
7.(4分)如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )
A.π B.2π C.3π D.4π
8.(4分)如果(x﹣4)(2x+3)=2x2﹣px+q,那么p,q的值分别是( )
A.5,12 B.﹣5,12 C.5,﹣12 D.﹣5,﹣12
9.(4分)若x2﹣mx+9是完全平方式,则m的值等于( )
A.6. B.﹣6 C.6或﹣6 D.12或﹣12
10.(4分)如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是( )
A.2α+∠A=180° B.α+∠A=90° C.2α+∠A=90° D.α+∠A=180°
二、填空题(本大题共6小题,每小题4分,共24分。)
11.(4分)计算:(﹣3)0= .
12.(4分)一个正n边形的一个外角等于72°,则n的值等于 .
13.(4分)已知AD为△ABC的中线,若△ABC的面积为8,则△ABD的面积是 .
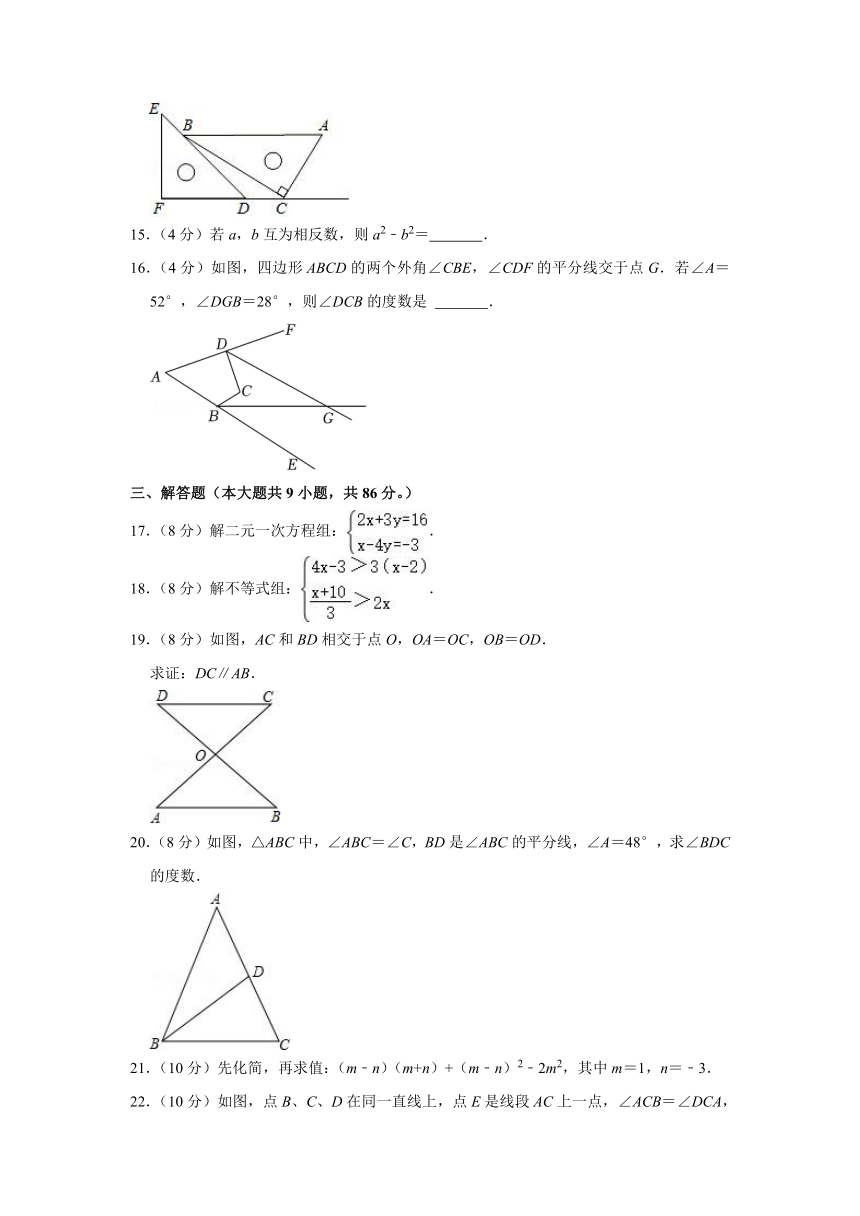
14.(4分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为 .
15.(4分)若a,b互为相反数,则a2﹣b2= .
16.(4分)如图,四边形ABCD的两个外角∠CBE,∠CDF的平分线交于点G.若∠A=52°,∠DGB=28°,则∠DCB的度数是 .
三、解答题(本大题共9小题,共86分。)
17.(8分)解二元一次方程组:.
18.(8分)解不等式组:.
19.(8分)如图,AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
20.(8分)如图,△ABC中,∠ABC=∠C,BD是∠ABC的平分线,∠A=48°,求∠BDC的度数.
21.(10分)先化简,再求值:(m﹣n)(m+n)+(m﹣n)2﹣2m2,其中m=1,n=﹣3.
22.(10分)如图,点B、C、D在同一直线上,点E是线段AC上一点,∠ACB=∠DCA,AB=DE,AC=CD,求证:∠A=∠D.
23.(10分)为了庆祝建团100周年,学校于5月4日举行知识竞赛活动,分两次购买了若干个排球和篮球做为奖品,第一次购买5个排球和6个篮球共840元,第二次以同样的价格购买同样的10个排球和9个篮球共1410元.
(1)求每个排球和篮球的单价各是多少元?
(2)根据学校的实际情况,需从该商店一次性购买排球和篮球共30个,要求购买排球和篮球的总费用不超过2200元,那么最多可以购买多少个篮球?
24.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠2=70°,求∠AEB的度数.
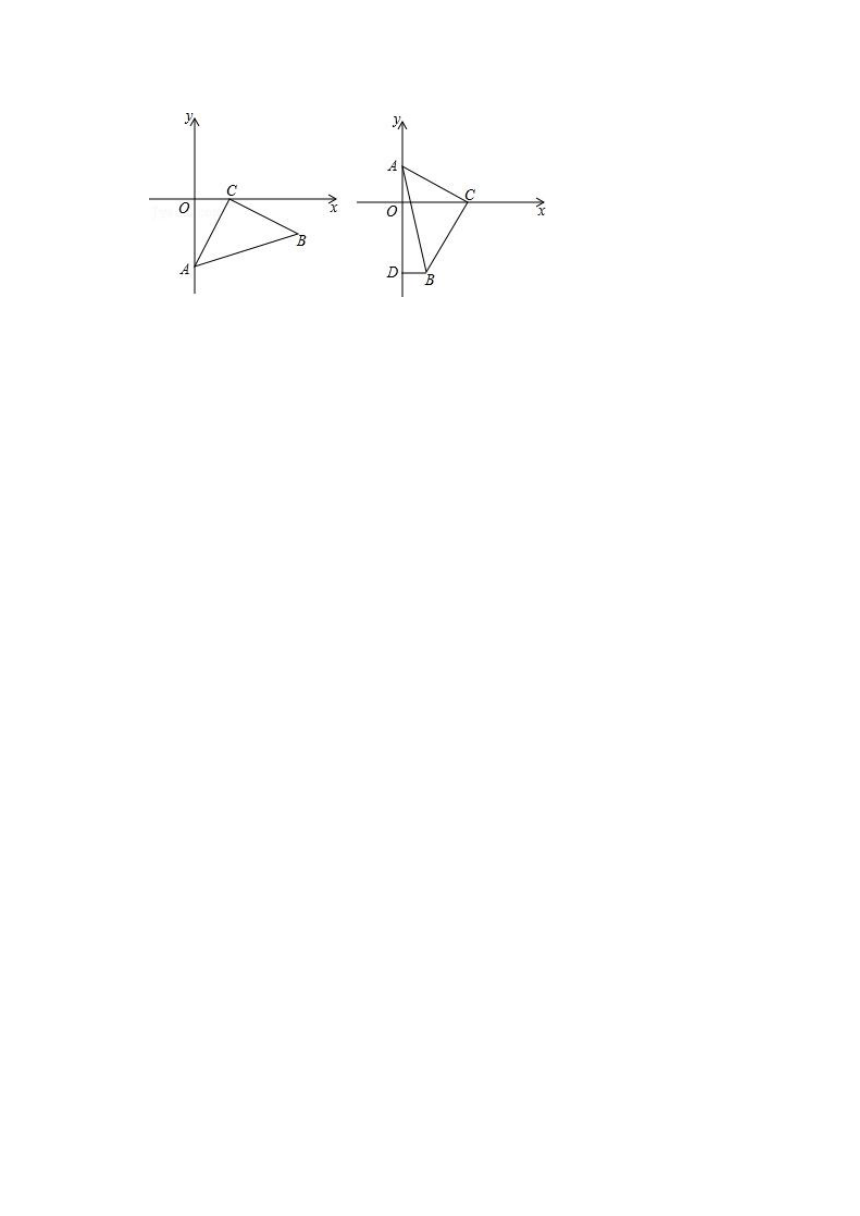
25.(14分)已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.
(1)如图1,当A(0,﹣2),C(1,0),点B在第四象限时,则点B的坐标为 ;
(2)如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断与哪一个是定值,并说明定值是多少?请证明你的结论.
2022-2023学年福建省福州四十中八年级(上)开门考数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分。)
1.(4分)下列图形具有稳定性的是( )
A. B.
C. D.
【分析】当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
【解答】解:∵三角形具有稳定性,
∴A选项符合题意而B,C,D选项不合题意.
故选:A.
【点评】本题主要考查了三角形的稳定性,解题时注意:三角形具有稳定性.
2.(4分)下列计算结果正确的是( )
A.b b3=b4 B.a8÷a4=a2
C.4a3 2a2=8a6 D.(2a3)2=4a5
【分析】A、根据单项式乘单项式的运算法则计算判断即可;B、根据单项式除单项式的运算法则计算判断即可;C、根据单项式乘单项式的运算法则计算判断即可;D、根据积的乘方与幂的乘方的运算法则计算判断即可.
【解答】解:A、原式=b4,符合题意;
B、原式=a4,不符合题意;
C、原式=8a5,不符合题意;
D、原式=4a6,不符合题意;
故选:A.
【点评】此题考查的是单项式乘单项式的运算、单项式除单项式的运算、积的乘方与幂的乘方的运算,掌握其运算法则是解决此题的关键.
3.(4分)下列等式从左到右的变形是因式分解的是( )
A.2x(x+3)=2x2+6x B.x2﹣y2=(x+y)(x﹣y)
C.x2+2xy+y2+1=(x+y)2+1 D.24xy2=3x 8y2
【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.
【解答】解:A、2x (x+3)=2x2+6x,是整式乘法,不是因式分解,故本选项不合题意;
B、x2﹣y2=(x+y) (x﹣y),是因式分解,故本选项符合题意;
C、x2+2xy+y2+1=(x+y) 2+1,等式的右边不是积的形式,不是因式分解,故本选项不合题意;
D、24xy2=3x 8y2,等式左边不是多项式,不是因式分解,故本选项不合题意;
故选:B.
【点评】本题考查了因式分解,因式分解是把一个多项式转化成几个整式积的形式.
4.(4分)如果等腰三角形的两边长分别3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15
【分析】由于等腰三角形的两边长分别是3和6,没有直接告诉哪一条是腰,哪一条是底边,所以有两种情况,分别利用三角形的周长的定义计算即可求解.
【解答】解:∵等腰三角形的两边长分别是3和6,
∴①当腰为6时,三角形的周长为:6+6+3=15;
②当腰为3时,3+3=6,三角形不成立;
∴此等腰三角形的周长是15.
故选:C.
【点评】此题主要考查了三角形的周长的计算,也利用了等腰三角形的性质,同时也利用了分类讨论的思想.
5.(4分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
【分析】要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.
【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;
故选:C.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
6.(4分)如图,在△ABC中,∠B=∠ACB=50°,P是边AB上的一个动点(不与顶点A重合),则∠BPC的度数可能是( )
A.50° B.80° C.100° D.130°
【分析】只要证明80°<∠BPC<130°即可解决问题.
【解答】解:∵∠B=∠ACB=50°,
∴∠A=180°﹣100°=80°,
∵∠BPC=∠A+∠ACP,
∴∠BPC>80°,
∵∠B+∠BPC+∠PCB=180°,
∴∠BPC<130°,
∴80°<∠BPC<130°,
故选:C.
【点评】本题考查等腰三角形的性质,三角形的内角和定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
7.(4分)如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )
A.π B.2π C.3π D.4π
【分析】根据三角形的外角和是360°以及扇形的面积公式,计算出阴影部分的面积和.
【解答】解:根据三角形的外角和是360°以及扇形的面积公式,得阴影部分的面积和是:=4π.
故选:D.
【点评】注意:根据扇形的面积公式,可以运用提公因式的方法把三个角整体加到一起进行计算.
8.(4分)如果(x﹣4)(2x+3)=2x2﹣px+q,那么p,q的值分别是( )
A.5,12 B.﹣5,12 C.5,﹣12 D.﹣5,﹣12
【分析】根据多项式乘多项式的乘法法则(a+b)(m+n)=am+an+bm+bn解决此题.
【解答】解:(x﹣4)(2x+3)=2x2+3x﹣8x﹣12=2x2﹣5x﹣12.
∵(x﹣4)(2x+3)=2x2﹣px+q,
∴﹣5=﹣p,q=﹣12.
∴p=5,q=﹣12.
故选:C.
【点评】本题主要考查多项式乘多项式,熟练掌握多项式乘多项式的乘法法则是解决本题的关键.
9.(4分)若x2﹣mx+9是完全平方式,则m的值等于( )
A.6. B.﹣6 C.6或﹣6 D.12或﹣12
【分析】利用完全平方公式的结构特征判断即可确定出m的值.
【解答】解:∵x2﹣mx+9是一个完全平方式,
∴m=±6.
故选:C.
【点评】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
10.(4分)如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是( )
A.2α+∠A=180° B.α+∠A=90° C.2α+∠A=90° D.α+∠A=180°
【分析】先证明△BDF≌△CED,得∠BFD=∠CDE,即可推导出α=∠B=∠C,由三角形内角和定理得∠B+∠C+∠A=180°,所以2α+∠A=180°,可判断A正确;
由2α+∠A=180°可推出α+∠A=90°,得α+∠A≠90°,可判断B错误;
由2α+∠A=180°可得2α+∠A≠90°,可判断C错误;
若α+∠A=180°,则∠C+∠B+∠A>180°,与三角形的内角和等于180°相矛盾,可见α+∠A≠180°,可判断D错误.
【解答】解:在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∴α=180°﹣∠CDE﹣∠BDF=180°﹣∠BFD﹣∠BDF=∠B=∠C,
∵∠B+∠C+∠A=180°,
∴2α+∠A=180°,
故A正确;
由2α+∠A=180°得α+∠A=90°,
∴α+∠A≠90°,
故B错误;
∵2α+∠A=180°,
∴2α+∠A≠90°,
故C错误;
若α+∠A=180°,
由∠B+∠A=180°,
∴∠C+∠B+∠A>180°,与三角形内角和定理相矛盾,
α+∠A≠180°,
故D错误,
故选:A.
【点评】此题重点考查全等三角形的判定与性质、三角形内角和定理等知识,通过证明△BDF≌△CED得到α=∠B=∠C是解题的关键.
二、填空题(本大题共6小题,每小题4分,共24分。)
11.(4分)计算:(﹣3)0= 1 .
【分析】根据零指数幂公式可得:(﹣3)0=1.
【解答】解:原式=1;
故答案为:1.
【点评】本题主要考查了零指数幂,任何非0数的0次幂等于1.
12.(4分)一个正n边形的一个外角等于72°,则n的值等于 5 .
【分析】可以利用多边形的外角和定理求解.
【解答】解:∵正n边形的一个外角为72°,
∴n的值为360°÷72°=5.
故答案为:5
【点评】本题考查了多边形外角和,熟记多边形的外角和等于360度是解题的关键.
13.(4分)已知AD为△ABC的中线,若△ABC的面积为8,则△ABD的面积是 4 .
【分析】设△ABC的高为h,S△ABD=BD×h=BC h,即可求解.
【解答】解:设△ABC的高为h,
S△ABD=BD×h=BC h=S△ABC=4,
故答案为4.
【点评】此题主要考查三角形的面积计算,关键是确定△ABC和△ABD时同高的关系,进而求解.
14.(4分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为 15° .
【分析】直接利用三角板的特点,结合平行线的性质得出∠ABD=45°,进而得出答案.
【解答】解:由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故答案为:15°.
【点评】此题主要考查了平行线的性质,根据题意得出∠ABD的度数是解题关键.
15.(4分)若a,b互为相反数,则a2﹣b2= 0 .
【分析】直接利用平方差公式分解因式进而结合相反数的定义分析得出答案.
【解答】解:∵a,b互为相反数,
∴a+b=0,
∴a2﹣b2=(a+b)(a﹣b)=0.
故答案为:0.
【点评】此题主要考查了公式法分解因式以及相反数的定义,正确分解因式是解题关键.
16.(4分)如图,四边形ABCD的两个外角∠CBE,∠CDF的平分线交于点G.若∠A=52°,∠DGB=28°,则∠DCB的度数是 108° .
【分析】连接AC,BD,由三角形外角定义可得∠FDC=∠DAC+∠DCA,∠CBE=∠BAC+∠BCA,再由DG平分∠FDC,BG平分∠CBE,可得∠CBG+∠CDG=(∠DAB+∠DCB),在△BDG中,根据三角形内角和定理可得∠G+∠CDG+∠CBE+∠CDB+∠DBC=180°,将式子进行等量代换即可求解.
【解答】解:连接AC,BD,
∴∠FDC=∠DAC+∠DCA,∠CBE=∠BAC+∠BCA,
∵DG平分∠FDC,BG平分∠CBE,
∴∠CBG+∠CDG=(∠DAB+∠DCB),
在△BDG中,∠G+∠CDG+∠CBE+∠CDB+∠DBC=180°,
∴∠G+(∠DAB+∠DCB)+∠CDB+∠DBC=180°,
∴∠G+(∠DAB+∠DCB)+(180°﹣∠DCB)=180°,
∵∠A=52°,∠DGB=28°,
∴28°+×52°+×∠DCB+180°﹣∠DCB=180°,
∴∠DCB=108°;
故答案为:108°.
【点评】本题考查三角形内角和定理,三角形外角定义;熟练掌握角平分线的性质,三角形的外角定义和三角形内角和定理,进行等量代换是求角的关键.
三、解答题(本大题共9小题,共86分。)
17.(8分)解二元一次方程组:.
【分析】②×2后字母x的系数为2,①的字母x的系数为2,两者相减即可消去字母x.
【解答】解:,
①﹣②×2,得11y=22,
解得y=2,
把y=2代入②,得x﹣8=﹣3,
解得x=5,
故原方程组的解为.
【点评】本题考查了二元一次方程组,掌握加减消元法是解决问题的关键.
18.(8分)解不等式组:.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:,
由①得:x>﹣3,
由②得:x<2,
则不等式组的解集为﹣3<x<2.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
19.(8分)如图,AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
【分析】由条件可证△AOB≌△COD,可求得∠A=∠C,则可证得DC∥AB.
【解答】证明:
在△ODC和△OBA中
∴△ODC≌△OBA (SAS);
∴∠C=∠A,
∴DC∥AB(内错角相等,两直线平行).
【点评】本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(全等三角形的对应边相等、对应角相等)是解题的关键.
20.(8分)如图,△ABC中,∠ABC=∠C,BD是∠ABC的平分线,∠A=48°,求∠BDC的度数.
【分析】由角平分线的定义可得:∠DBC=∠ABC,然后设∠DBC=x,则∠ABC=∠C=2x,∠BDC=x+48°,然后在△BCD中,根据三角形内角和定理可求x的值,即可确定∠ABD的度数,然后根据三角形外角的性质即可求∠BDC的度数.
【解答】解:∵BD是∠ABC的平分线
∴∠ABD=∠DBC,
∵∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
设∠DBC=∠DBC=x,则∠ABC=∠ACB=2x,
∵∠BDC=∠ABD+∠A,∠A=48°,
∴∠BDC=x+48°,
∵∠DBC+∠ACB+∠BDC=180°,
∴x+2x+x+48°=180°
∴x=33°,
∴∠BDC=33°+48°=81°.
【点评】此题主要考查等腰三角形的性质,三角形内角和定理及三角形外角的性质的综合运用,解题的关键是熟练掌握三角形的性质.
21.(10分)先化简,再求值:(m﹣n)(m+n)+(m﹣n)2﹣2m2,其中m=1,n=﹣3.
【分析】原式第一项利用平方差公式化简,第二项利用完全平方公式展开,去括号合并得到最简结果,将m与n的值代入计算即可求出值.
【解答】解:原式=m2﹣n2+m2﹣2mn+n2﹣2m2
=﹣2mn,
当m=1,n=﹣3时,原式=6.
【点评】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
22.(10分)如图,点B、C、D在同一直线上,点E是线段AC上一点,∠ACB=∠DCA,AB=DE,AC=CD,求证:∠A=∠D.
【分析】首先根据平角的定义可得∠ACB=∠DCA=90°,再利用HL证明Rt△ABC≌Rt△DEC,即可得出结论.
【解答】证明:∵点B、C、D在同一直线上,∠ACB=∠DCA,
∴∠ACB=∠DCA=90°,
在Rt△ABC和Rt△DEC中,
,
∴Rt△ABC≌Rt△DEC(HL),
∴∠A=∠D.
【点评】本题主要考查了全等三角形的判定与性质,平角的定义等知识,熟练掌握全等三角形的判定与性质是解题的关键.
23.(10分)为了庆祝建团100周年,学校于5月4日举行知识竞赛活动,分两次购买了若干个排球和篮球做为奖品,第一次购买5个排球和6个篮球共840元,第二次以同样的价格购买同样的10个排球和9个篮球共1410元.
(1)求每个排球和篮球的单价各是多少元?
(2)根据学校的实际情况,需从该商店一次性购买排球和篮球共30个,要求购买排球和篮球的总费用不超过2200元,那么最多可以购买多少个篮球?
【分析】(1)设每个排球x元,每个篮球y元,根据“购买5个排球和6个篮球共需840元,购买10个排球和9个篮球共需1410元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买篮球a个,则购买排球(30﹣a)个,根据总价=单价×数量结合购买排球和篮球的总费用不超过2200元,即可得出关于a的一元一次不等式,解之取其中的最大值整数值即可得出结论.
【解答】解:(1)设每个排球x元,每个篮球y元,
依题意,得:,
解得:,
答:设每个排球60元,每个篮球90元.
(2)设购买篮球a个,则购买排球(30﹣a)个,
依题意,得:90a+60(30﹣a)≤2200,
解得:a≤13.3.
∵a为整数,
∴a最大取13.
答:最多可以买13个篮球.
【点评】本题考查了二元一次方程组的应用、一元一次不等式的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
24.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠2=70°,求∠AEB的度数.
【分析】(1)利用三角形外角的性质得∠BDE=∠C,再利用AAS证明△AEC≌△BED即可;
(2)由全等三角形的性质得∠BED=∠AEC,则∠BEA=∠2=70°.
【解答】(1)证明:∵∠ADB=∠2+∠C=∠1+∠BDE,∠1=∠2,
∴∠BDE=∠C,
在△AEC和△BED中,
,
∴△AEC≌△BED(AAS);
(2)解:∵△AEC≌△BED,
∴∠BED=∠AEC,
∴∠BEA=∠2,
∵∠2=70°,
∴∠AEB=70°.
【点评】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
25.(14分)已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.
(1)如图1,当A(0,﹣2),C(1,0),点B在第四象限时,则点B的坐标为 (3,﹣1), ;
(2)如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断与哪一个是定值,并说明定值是多少?请证明你的结论.
【分析】(1)过B作BE⊥x轴于E,推出∠2=∠OAC,∠AOC=∠BEC,根据AAS证△AOC≌△CEB,推出OA=CE,OC=BE,根据A、C的坐标即可求出答案;
(2)作BE⊥x轴于E,得出矩形OEBD,推出BD=OE,证△CEB≌△AOC,推出AO=CE,求出OC﹣BD=OA,代入求出即可.
【解答】(1)解:过B作BE⊥x轴于E,
则∠BEC=∠ACB=∠AOC=90°,
∴∠1+∠2=90°,∠1+∠OAC=90°,
∴∠2=∠OAC,
在△AOC和△CEB中
∵,
∴△AOC≌△CEB(AAS),
∴OA=CE,OC=BE,
∵A(0,﹣2),C(1,0),
∴OA=CE=2,OC=BE=1,
∴OE=1+2=3,
∴点B的坐标为( 3,﹣1 );
(2)结论:,
证明:作BE⊥x轴于E,
∴∠1=90°=∠2,
∴∠3+∠4=90°,
∵∠ACB=90°,
∴∠5+∠3=90°,
∴∠5=∠4,
在△CEB和△AOC中,
∵
∴△CEB≌△AOC,
∴AO=CE,
∵BE⊥x轴于E,
∴BE∥y轴,
∵BD⊥y轴于点D,EO⊥y轴于点O,
∴BD∥OE,
∴四边形OEBD是矩形,
∴EO=BD,
∴OC﹣BD=OC﹣EO=CE=AO,
∴.
【点评】本题考查了全等三角形的性质和判定,坐标与图形性质,等腰直角三角形性质,主要考查学生运用定理进行推理和计算,题目比较好.
(附答案解析)
一、选择题(本大题共10小题,每小题4分,共40分。)
1.(4分)下列图形具有稳定性的是( )
A. B.
C. D.
2.(4分)下列计算结果正确的是( )
A.b b3=b4 B.a8÷a4=a2
C.4a3 2a2=8a6 D.(2a3)2=4a5
3.(4分)下列等式从左到右的变形是因式分解的是( )
A.2x(x+3)=2x2+6x B.x2﹣y2=(x+y)(x﹣y)
C.x2+2xy+y2+1=(x+y)2+1 D.24xy2=3x 8y2
4.(4分)如果等腰三角形的两边长分别3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15
5.(4分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
6.(4分)如图,在△ABC中,∠B=∠ACB=50°,P是边AB上的一个动点(不与顶点A重合),则∠BPC的度数可能是( )
A.50° B.80° C.100° D.130°
7.(4分)如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )
A.π B.2π C.3π D.4π
8.(4分)如果(x﹣4)(2x+3)=2x2﹣px+q,那么p,q的值分别是( )
A.5,12 B.﹣5,12 C.5,﹣12 D.﹣5,﹣12
9.(4分)若x2﹣mx+9是完全平方式,则m的值等于( )
A.6. B.﹣6 C.6或﹣6 D.12或﹣12
10.(4分)如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是( )
A.2α+∠A=180° B.α+∠A=90° C.2α+∠A=90° D.α+∠A=180°
二、填空题(本大题共6小题,每小题4分,共24分。)
11.(4分)计算:(﹣3)0= .
12.(4分)一个正n边形的一个外角等于72°,则n的值等于 .
13.(4分)已知AD为△ABC的中线,若△ABC的面积为8,则△ABD的面积是 .
14.(4分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为 .
15.(4分)若a,b互为相反数,则a2﹣b2= .
16.(4分)如图,四边形ABCD的两个外角∠CBE,∠CDF的平分线交于点G.若∠A=52°,∠DGB=28°,则∠DCB的度数是 .
三、解答题(本大题共9小题,共86分。)
17.(8分)解二元一次方程组:.
18.(8分)解不等式组:.
19.(8分)如图,AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
20.(8分)如图,△ABC中,∠ABC=∠C,BD是∠ABC的平分线,∠A=48°,求∠BDC的度数.
21.(10分)先化简,再求值:(m﹣n)(m+n)+(m﹣n)2﹣2m2,其中m=1,n=﹣3.
22.(10分)如图,点B、C、D在同一直线上,点E是线段AC上一点,∠ACB=∠DCA,AB=DE,AC=CD,求证:∠A=∠D.
23.(10分)为了庆祝建团100周年,学校于5月4日举行知识竞赛活动,分两次购买了若干个排球和篮球做为奖品,第一次购买5个排球和6个篮球共840元,第二次以同样的价格购买同样的10个排球和9个篮球共1410元.
(1)求每个排球和篮球的单价各是多少元?
(2)根据学校的实际情况,需从该商店一次性购买排球和篮球共30个,要求购买排球和篮球的总费用不超过2200元,那么最多可以购买多少个篮球?
24.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠2=70°,求∠AEB的度数.
25.(14分)已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.
(1)如图1,当A(0,﹣2),C(1,0),点B在第四象限时,则点B的坐标为 ;
(2)如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断与哪一个是定值,并说明定值是多少?请证明你的结论.
2022-2023学年福建省福州四十中八年级(上)开门考数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分。)
1.(4分)下列图形具有稳定性的是( )
A. B.
C. D.
【分析】当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
【解答】解:∵三角形具有稳定性,
∴A选项符合题意而B,C,D选项不合题意.
故选:A.
【点评】本题主要考查了三角形的稳定性,解题时注意:三角形具有稳定性.
2.(4分)下列计算结果正确的是( )
A.b b3=b4 B.a8÷a4=a2
C.4a3 2a2=8a6 D.(2a3)2=4a5
【分析】A、根据单项式乘单项式的运算法则计算判断即可;B、根据单项式除单项式的运算法则计算判断即可;C、根据单项式乘单项式的运算法则计算判断即可;D、根据积的乘方与幂的乘方的运算法则计算判断即可.
【解答】解:A、原式=b4,符合题意;
B、原式=a4,不符合题意;
C、原式=8a5,不符合题意;
D、原式=4a6,不符合题意;
故选:A.
【点评】此题考查的是单项式乘单项式的运算、单项式除单项式的运算、积的乘方与幂的乘方的运算,掌握其运算法则是解决此题的关键.
3.(4分)下列等式从左到右的变形是因式分解的是( )
A.2x(x+3)=2x2+6x B.x2﹣y2=(x+y)(x﹣y)
C.x2+2xy+y2+1=(x+y)2+1 D.24xy2=3x 8y2
【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.
【解答】解:A、2x (x+3)=2x2+6x,是整式乘法,不是因式分解,故本选项不合题意;
B、x2﹣y2=(x+y) (x﹣y),是因式分解,故本选项符合题意;
C、x2+2xy+y2+1=(x+y) 2+1,等式的右边不是积的形式,不是因式分解,故本选项不合题意;
D、24xy2=3x 8y2,等式左边不是多项式,不是因式分解,故本选项不合题意;
故选:B.
【点评】本题考查了因式分解,因式分解是把一个多项式转化成几个整式积的形式.
4.(4分)如果等腰三角形的两边长分别3和6,则它的周长为( )
A.9 B.12 C.15 D.12或15
【分析】由于等腰三角形的两边长分别是3和6,没有直接告诉哪一条是腰,哪一条是底边,所以有两种情况,分别利用三角形的周长的定义计算即可求解.
【解答】解:∵等腰三角形的两边长分别是3和6,
∴①当腰为6时,三角形的周长为:6+6+3=15;
②当腰为3时,3+3=6,三角形不成立;
∴此等腰三角形的周长是15.
故选:C.
【点评】此题主要考查了三角形的周长的计算,也利用了等腰三角形的性质,同时也利用了分类讨论的思想.
5.(4分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
【分析】要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.
【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;
故选:C.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
6.(4分)如图,在△ABC中,∠B=∠ACB=50°,P是边AB上的一个动点(不与顶点A重合),则∠BPC的度数可能是( )
A.50° B.80° C.100° D.130°
【分析】只要证明80°<∠BPC<130°即可解决问题.
【解答】解:∵∠B=∠ACB=50°,
∴∠A=180°﹣100°=80°,
∵∠BPC=∠A+∠ACP,
∴∠BPC>80°,
∵∠B+∠BPC+∠PCB=180°,
∴∠BPC<130°,
∴80°<∠BPC<130°,
故选:C.
【点评】本题考查等腰三角形的性质,三角形的内角和定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
7.(4分)如图,以三角形三个顶点为圆心画半径为2的圆,则阴影部分面积之和为( )
A.π B.2π C.3π D.4π
【分析】根据三角形的外角和是360°以及扇形的面积公式,计算出阴影部分的面积和.
【解答】解:根据三角形的外角和是360°以及扇形的面积公式,得阴影部分的面积和是:=4π.
故选:D.
【点评】注意:根据扇形的面积公式,可以运用提公因式的方法把三个角整体加到一起进行计算.
8.(4分)如果(x﹣4)(2x+3)=2x2﹣px+q,那么p,q的值分别是( )
A.5,12 B.﹣5,12 C.5,﹣12 D.﹣5,﹣12
【分析】根据多项式乘多项式的乘法法则(a+b)(m+n)=am+an+bm+bn解决此题.
【解答】解:(x﹣4)(2x+3)=2x2+3x﹣8x﹣12=2x2﹣5x﹣12.
∵(x﹣4)(2x+3)=2x2﹣px+q,
∴﹣5=﹣p,q=﹣12.
∴p=5,q=﹣12.
故选:C.
【点评】本题主要考查多项式乘多项式,熟练掌握多项式乘多项式的乘法法则是解决本题的关键.
9.(4分)若x2﹣mx+9是完全平方式,则m的值等于( )
A.6. B.﹣6 C.6或﹣6 D.12或﹣12
【分析】利用完全平方公式的结构特征判断即可确定出m的值.
【解答】解:∵x2﹣mx+9是一个完全平方式,
∴m=±6.
故选:C.
【点评】此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
10.(4分)如图,在△ABC中,∠B=∠C,BF=CD,BD=CE,∠FDE=α,则下列结论正确的是( )
A.2α+∠A=180° B.α+∠A=90° C.2α+∠A=90° D.α+∠A=180°
【分析】先证明△BDF≌△CED,得∠BFD=∠CDE,即可推导出α=∠B=∠C,由三角形内角和定理得∠B+∠C+∠A=180°,所以2α+∠A=180°,可判断A正确;
由2α+∠A=180°可推出α+∠A=90°,得α+∠A≠90°,可判断B错误;
由2α+∠A=180°可得2α+∠A≠90°,可判断C错误;
若α+∠A=180°,则∠C+∠B+∠A>180°,与三角形的内角和等于180°相矛盾,可见α+∠A≠180°,可判断D错误.
【解答】解:在△BDF和△CED中,
,
∴△BDF≌△CED(SAS),
∴∠BFD=∠CDE,
∴α=180°﹣∠CDE﹣∠BDF=180°﹣∠BFD﹣∠BDF=∠B=∠C,
∵∠B+∠C+∠A=180°,
∴2α+∠A=180°,
故A正确;
由2α+∠A=180°得α+∠A=90°,
∴α+∠A≠90°,
故B错误;
∵2α+∠A=180°,
∴2α+∠A≠90°,
故C错误;
若α+∠A=180°,
由∠B+∠A=180°,
∴∠C+∠B+∠A>180°,与三角形内角和定理相矛盾,
α+∠A≠180°,
故D错误,
故选:A.
【点评】此题重点考查全等三角形的判定与性质、三角形内角和定理等知识,通过证明△BDF≌△CED得到α=∠B=∠C是解题的关键.
二、填空题(本大题共6小题,每小题4分,共24分。)
11.(4分)计算:(﹣3)0= 1 .
【分析】根据零指数幂公式可得:(﹣3)0=1.
【解答】解:原式=1;
故答案为:1.
【点评】本题主要考查了零指数幂,任何非0数的0次幂等于1.
12.(4分)一个正n边形的一个外角等于72°,则n的值等于 5 .
【分析】可以利用多边形的外角和定理求解.
【解答】解:∵正n边形的一个外角为72°,
∴n的值为360°÷72°=5.
故答案为:5
【点评】本题考查了多边形外角和,熟记多边形的外角和等于360度是解题的关键.
13.(4分)已知AD为△ABC的中线,若△ABC的面积为8,则△ABD的面积是 4 .
【分析】设△ABC的高为h,S△ABD=BD×h=BC h,即可求解.
【解答】解:设△ABC的高为h,
S△ABD=BD×h=BC h=S△ABC=4,
故答案为4.
【点评】此题主要考查三角形的面积计算,关键是确定△ABC和△ABD时同高的关系,进而求解.
14.(4分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为 15° .
【分析】直接利用三角板的特点,结合平行线的性质得出∠ABD=45°,进而得出答案.
【解答】解:由题意可得:∠EDF=45°,∠ABC=30°,
∵AB∥CF,
∴∠ABD=∠EDF=45°,
∴∠DBC=45°﹣30°=15°.
故答案为:15°.
【点评】此题主要考查了平行线的性质,根据题意得出∠ABD的度数是解题关键.
15.(4分)若a,b互为相反数,则a2﹣b2= 0 .
【分析】直接利用平方差公式分解因式进而结合相反数的定义分析得出答案.
【解答】解:∵a,b互为相反数,
∴a+b=0,
∴a2﹣b2=(a+b)(a﹣b)=0.
故答案为:0.
【点评】此题主要考查了公式法分解因式以及相反数的定义,正确分解因式是解题关键.
16.(4分)如图,四边形ABCD的两个外角∠CBE,∠CDF的平分线交于点G.若∠A=52°,∠DGB=28°,则∠DCB的度数是 108° .
【分析】连接AC,BD,由三角形外角定义可得∠FDC=∠DAC+∠DCA,∠CBE=∠BAC+∠BCA,再由DG平分∠FDC,BG平分∠CBE,可得∠CBG+∠CDG=(∠DAB+∠DCB),在△BDG中,根据三角形内角和定理可得∠G+∠CDG+∠CBE+∠CDB+∠DBC=180°,将式子进行等量代换即可求解.
【解答】解:连接AC,BD,
∴∠FDC=∠DAC+∠DCA,∠CBE=∠BAC+∠BCA,
∵DG平分∠FDC,BG平分∠CBE,
∴∠CBG+∠CDG=(∠DAB+∠DCB),
在△BDG中,∠G+∠CDG+∠CBE+∠CDB+∠DBC=180°,
∴∠G+(∠DAB+∠DCB)+∠CDB+∠DBC=180°,
∴∠G+(∠DAB+∠DCB)+(180°﹣∠DCB)=180°,
∵∠A=52°,∠DGB=28°,
∴28°+×52°+×∠DCB+180°﹣∠DCB=180°,
∴∠DCB=108°;
故答案为:108°.
【点评】本题考查三角形内角和定理,三角形外角定义;熟练掌握角平分线的性质,三角形的外角定义和三角形内角和定理,进行等量代换是求角的关键.
三、解答题(本大题共9小题,共86分。)
17.(8分)解二元一次方程组:.
【分析】②×2后字母x的系数为2,①的字母x的系数为2,两者相减即可消去字母x.
【解答】解:,
①﹣②×2,得11y=22,
解得y=2,
把y=2代入②,得x﹣8=﹣3,
解得x=5,
故原方程组的解为.
【点评】本题考查了二元一次方程组,掌握加减消元法是解决问题的关键.
18.(8分)解不等式组:.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解答】解:,
由①得:x>﹣3,
由②得:x<2,
则不等式组的解集为﹣3<x<2.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
19.(8分)如图,AC和BD相交于点O,OA=OC,OB=OD.
求证:DC∥AB.
【分析】由条件可证△AOB≌△COD,可求得∠A=∠C,则可证得DC∥AB.
【解答】证明:
在△ODC和△OBA中
∴△ODC≌△OBA (SAS);
∴∠C=∠A,
∴DC∥AB(内错角相等,两直线平行).
【点评】本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(全等三角形的对应边相等、对应角相等)是解题的关键.
20.(8分)如图,△ABC中,∠ABC=∠C,BD是∠ABC的平分线,∠A=48°,求∠BDC的度数.
【分析】由角平分线的定义可得:∠DBC=∠ABC,然后设∠DBC=x,则∠ABC=∠C=2x,∠BDC=x+48°,然后在△BCD中,根据三角形内角和定理可求x的值,即可确定∠ABD的度数,然后根据三角形外角的性质即可求∠BDC的度数.
【解答】解:∵BD是∠ABC的平分线
∴∠ABD=∠DBC,
∵∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
设∠DBC=∠DBC=x,则∠ABC=∠ACB=2x,
∵∠BDC=∠ABD+∠A,∠A=48°,
∴∠BDC=x+48°,
∵∠DBC+∠ACB+∠BDC=180°,
∴x+2x+x+48°=180°
∴x=33°,
∴∠BDC=33°+48°=81°.
【点评】此题主要考查等腰三角形的性质,三角形内角和定理及三角形外角的性质的综合运用,解题的关键是熟练掌握三角形的性质.
21.(10分)先化简,再求值:(m﹣n)(m+n)+(m﹣n)2﹣2m2,其中m=1,n=﹣3.
【分析】原式第一项利用平方差公式化简,第二项利用完全平方公式展开,去括号合并得到最简结果,将m与n的值代入计算即可求出值.
【解答】解:原式=m2﹣n2+m2﹣2mn+n2﹣2m2
=﹣2mn,
当m=1,n=﹣3时,原式=6.
【点评】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
22.(10分)如图,点B、C、D在同一直线上,点E是线段AC上一点,∠ACB=∠DCA,AB=DE,AC=CD,求证:∠A=∠D.
【分析】首先根据平角的定义可得∠ACB=∠DCA=90°,再利用HL证明Rt△ABC≌Rt△DEC,即可得出结论.
【解答】证明:∵点B、C、D在同一直线上,∠ACB=∠DCA,
∴∠ACB=∠DCA=90°,
在Rt△ABC和Rt△DEC中,
,
∴Rt△ABC≌Rt△DEC(HL),
∴∠A=∠D.
【点评】本题主要考查了全等三角形的判定与性质,平角的定义等知识,熟练掌握全等三角形的判定与性质是解题的关键.
23.(10分)为了庆祝建团100周年,学校于5月4日举行知识竞赛活动,分两次购买了若干个排球和篮球做为奖品,第一次购买5个排球和6个篮球共840元,第二次以同样的价格购买同样的10个排球和9个篮球共1410元.
(1)求每个排球和篮球的单价各是多少元?
(2)根据学校的实际情况,需从该商店一次性购买排球和篮球共30个,要求购买排球和篮球的总费用不超过2200元,那么最多可以购买多少个篮球?
【分析】(1)设每个排球x元,每个篮球y元,根据“购买5个排球和6个篮球共需840元,购买10个排球和9个篮球共需1410元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买篮球a个,则购买排球(30﹣a)个,根据总价=单价×数量结合购买排球和篮球的总费用不超过2200元,即可得出关于a的一元一次不等式,解之取其中的最大值整数值即可得出结论.
【解答】解:(1)设每个排球x元,每个篮球y元,
依题意,得:,
解得:,
答:设每个排球60元,每个篮球90元.
(2)设购买篮球a个,则购买排球(30﹣a)个,
依题意,得:90a+60(30﹣a)≤2200,
解得:a≤13.3.
∵a为整数,
∴a最大取13.
答:最多可以买13个篮球.
【点评】本题考查了二元一次方程组的应用、一元一次不等式的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
24.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠2=70°,求∠AEB的度数.
【分析】(1)利用三角形外角的性质得∠BDE=∠C,再利用AAS证明△AEC≌△BED即可;
(2)由全等三角形的性质得∠BED=∠AEC,则∠BEA=∠2=70°.
【解答】(1)证明:∵∠ADB=∠2+∠C=∠1+∠BDE,∠1=∠2,
∴∠BDE=∠C,
在△AEC和△BED中,
,
∴△AEC≌△BED(AAS);
(2)解:∵△AEC≌△BED,
∴∠BED=∠AEC,
∴∠BEA=∠2,
∵∠2=70°,
∴∠AEB=70°.
【点评】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
25.(14分)已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.
(1)如图1,当A(0,﹣2),C(1,0),点B在第四象限时,则点B的坐标为 (3,﹣1), ;
(2)如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断与哪一个是定值,并说明定值是多少?请证明你的结论.
【分析】(1)过B作BE⊥x轴于E,推出∠2=∠OAC,∠AOC=∠BEC,根据AAS证△AOC≌△CEB,推出OA=CE,OC=BE,根据A、C的坐标即可求出答案;
(2)作BE⊥x轴于E,得出矩形OEBD,推出BD=OE,证△CEB≌△AOC,推出AO=CE,求出OC﹣BD=OA,代入求出即可.
【解答】(1)解:过B作BE⊥x轴于E,
则∠BEC=∠ACB=∠AOC=90°,
∴∠1+∠2=90°,∠1+∠OAC=90°,
∴∠2=∠OAC,
在△AOC和△CEB中
∵,
∴△AOC≌△CEB(AAS),
∴OA=CE,OC=BE,
∵A(0,﹣2),C(1,0),
∴OA=CE=2,OC=BE=1,
∴OE=1+2=3,
∴点B的坐标为( 3,﹣1 );
(2)结论:,
证明:作BE⊥x轴于E,
∴∠1=90°=∠2,
∴∠3+∠4=90°,
∵∠ACB=90°,
∴∠5+∠3=90°,
∴∠5=∠4,
在△CEB和△AOC中,
∵
∴△CEB≌△AOC,
∴AO=CE,
∵BE⊥x轴于E,
∴BE∥y轴,
∵BD⊥y轴于点D,EO⊥y轴于点O,
∴BD∥OE,
∴四边形OEBD是矩形,
∴EO=BD,
∴OC﹣BD=OC﹣EO=CE=AO,
∴.
【点评】本题考查了全等三角形的性质和判定,坐标与图形性质,等腰直角三角形性质,主要考查学生运用定理进行推理和计算,题目比较好.
同课章节目录
