简单的轴对称图形[下学期]

课题 简单的轴对称图形（一） 课型 新授课
内容 第2册第7单元第2节第1课总第4课时 课时 1课时
教学目标 经历探索简单的轴对称性的过程；进一步体验轴对称的特征，发展空间观念。探索并了解角的平分线，线段的垂直平分线的有关性质，并能适当地进行简单应用。3. 通过活动培养学生研究轴对称图形的思想方法。
教学重点 探索并了解角的平分线，线段的垂直平分线的有关性质
教学难点 通过操作，理解结论产生的过程
教学方法 观察----动手----交流-----探索相结合
教学手段 课件、板书、多媒体
教学过程 教师活动 学生活动 教学意图 备注
复习联想情境引入 轴对称图形的概念和对称轴的概念。生活中的轴对称图形的实例。几何中有否有轴对称图形？ 积极回忆畅所欲言积极思考 联系上节课的知识，自然导入。 为下面的问题做个铺垫
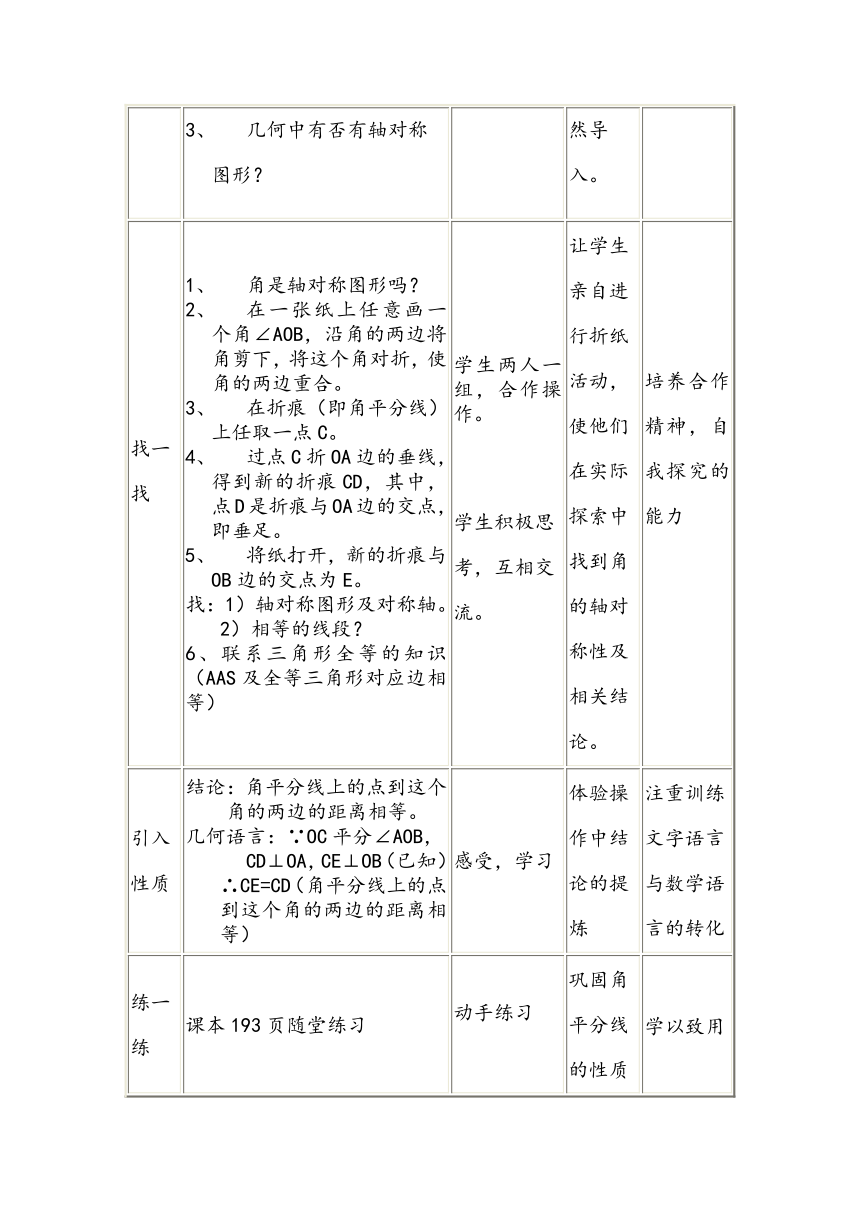
找一找 角是轴对称图形吗？在一张纸上任意画一个角∠AOB，沿角的两边将角剪下，将这个角对折，使角的两边重合。在折痕（即角平分线）上任取一点C。过点C折OA边的垂线，得到新的折痕CD，其中，点D是折痕与OA边的交点，即垂足。将纸打开，新的折痕与OB边的交点为E。找：1）轴对称图形及对称轴。2）相等的线段？6、联系三角形全等的知识（AAS及全等三角形对应边相等） 学生两人一组，合作操作。学生积极思考，互相交流。 让学生亲自进行折纸活动，使他们在实际探索中找到角的轴对称性及相关结论。 培养合作精神，自我探究的能力
引入性质 结论：角平分线上的点到这个角的两边的距离相等。几何语言：∵OC平分∠AOB，CD⊥OA，CE⊥OB（已知）∴CE=CD（角平分线上的点到这个角的两边的距离相等） 感受，学习 体验操作中结论的提炼 注重训练文字语言与数学语言的转化
练一练 课本193页随堂练习 动手练习 巩固角平分线的性质 学以致用
折一折 线段是轴对称图形吗？你能利用折纸的方法将线段AB分成两段彼此相等的线段吗？画一线段AB，对折后使点A、B重合，折痕与AB的交点为O；在折痕上任取一点C，沿CA将纸折叠。将纸展开CA和CB。问：1）CO与AB有怎样的位置关系？2）AO与OB相等吗？CA与CB呢？探索理由。3）线段是轴对称图形吗？对称轴在哪？4、联系三角形全等的知识（SAS及全等三角形的对应边相等） 学生动手操作 使学生进一步进行折纸活动，体会相关结论。 培养合作精神，自我探究的能力
概念及性质引入 垂直且平分这条线段的直线叫做这条线段的垂直平分线，即中垂线。线段垂直平分线上的点到这条线段两个端点的距离相等。几何语言：∵OD垂直平分AB（已知）∴AD=AB（线段垂直平分线上的点到这条线段两个端点的距离相等） 体会学习 体验操作中结论的提炼 注重训练文字语言与数学语言的转化
练一练 见幻灯片练习 思考练习 巩固垂直平分线的性质及角平分线的性质 学以致用
谈一谈 同学们，这节课你有什么体会和收获呢？ 交流并发言 回顾小结
布置作业 课课练：简单的轴对称图形（一） 巩固、反馈 并培养学生对所学内容的反思和评价。
机动内容 学习几何语言的叙述时要留有充分多的时间，黑板板书，让学生模仿，并根据学生的具体情况，给与订正。
作业 课课练：简单的轴对称图形（一）
板书设计 1、角平分线上的点到这个角的两边的距离相等。2、线段垂直平分线上的点到这条线段两个端点的距离相等。