1.2一定是直角三角形吗 课件

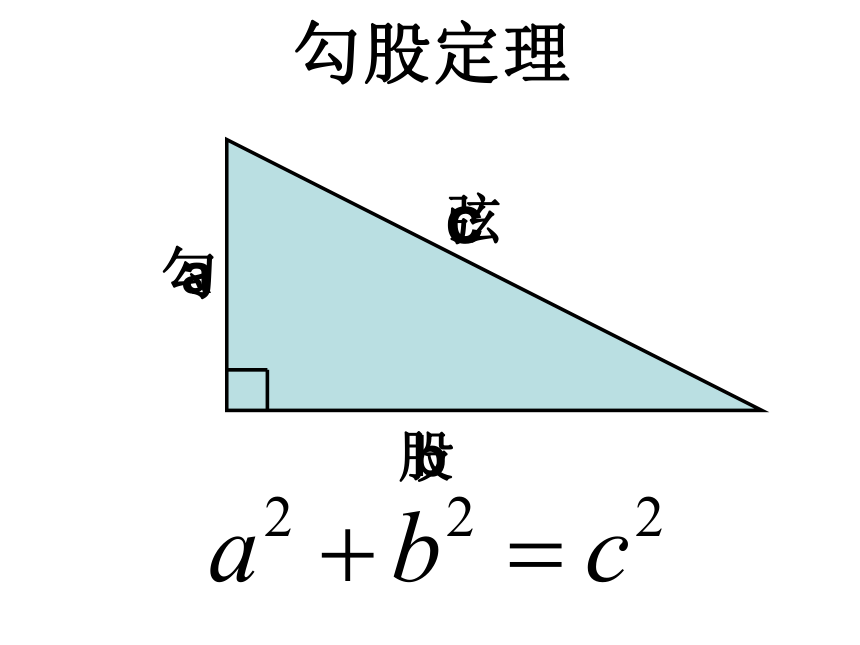
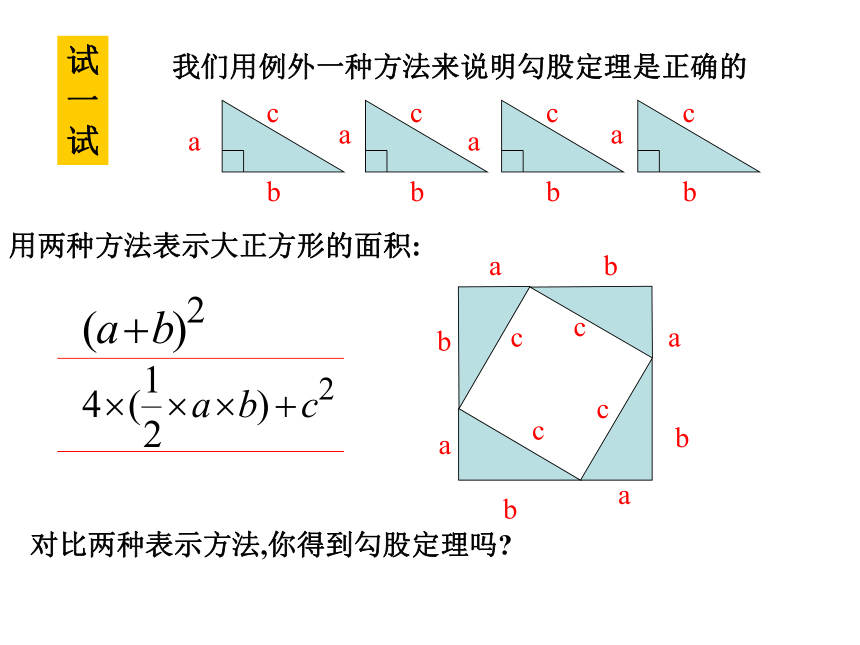
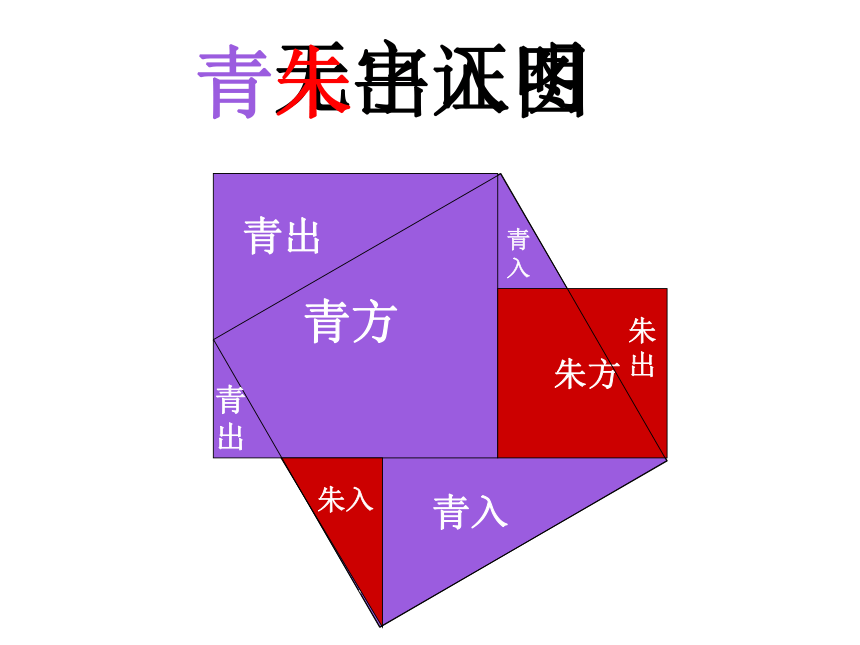
课件23张PPT。勾股定理abc勾股弦用两种方法表示大正方形的面积:对比两种表示方法,你得到勾股定理吗?试
一
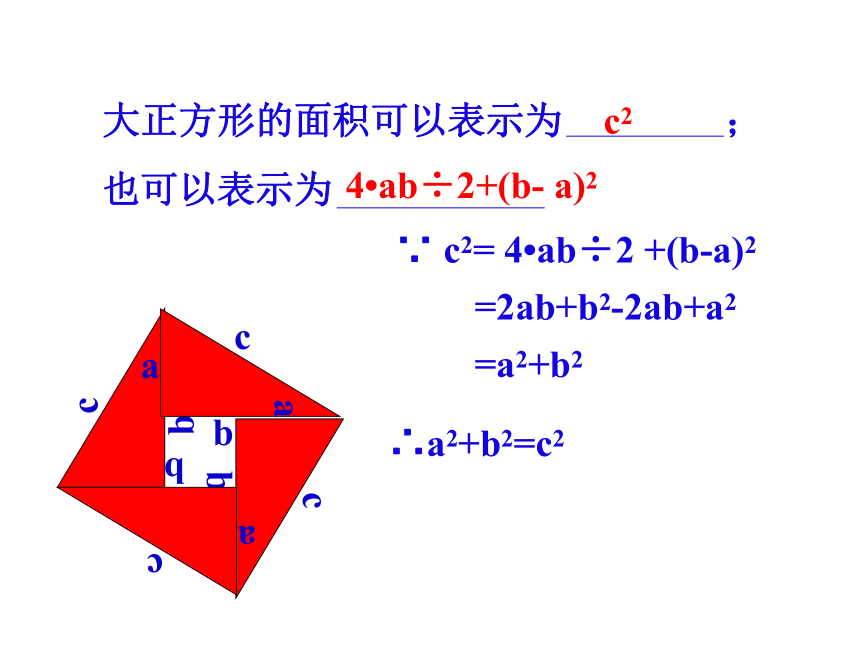
试我们用例外一种方法来说明勾股定理是正确的∵ c2= 4?ab÷2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为c24?ab÷2+(b- a)2
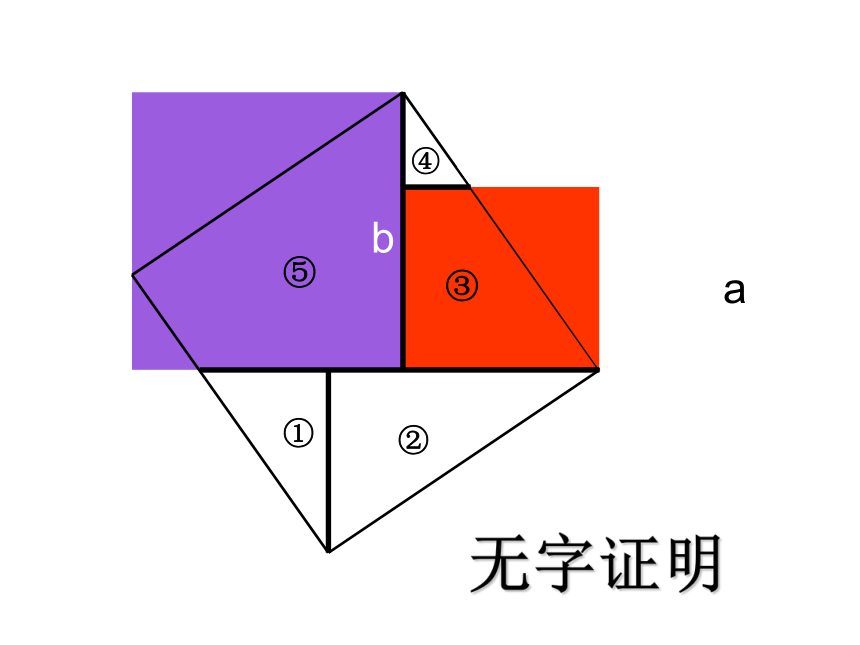
abc无字证明无字证明青出青朱出入图1、勾股定理的前提条件是什么？直角三角形 两直角边的平方和等于斜边的平方2、反过来，如果一个三角形满足了“两直角边的平方和等于斜边的平方”，那么它一定是直角三角形吗？做 一 做 下列的五组数分别是一个三角形
的三边长a，b，c：
①3，4，5； ②6，8，10；③5，12，13；
④7，24，25； ⑤ 8，15，17
（1）这三组数都满足a2+b2=c2吗？
（2）分别以每组数为三边作出三角形，用
量角器量一量，它们都是直角三角形吗？ 如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是
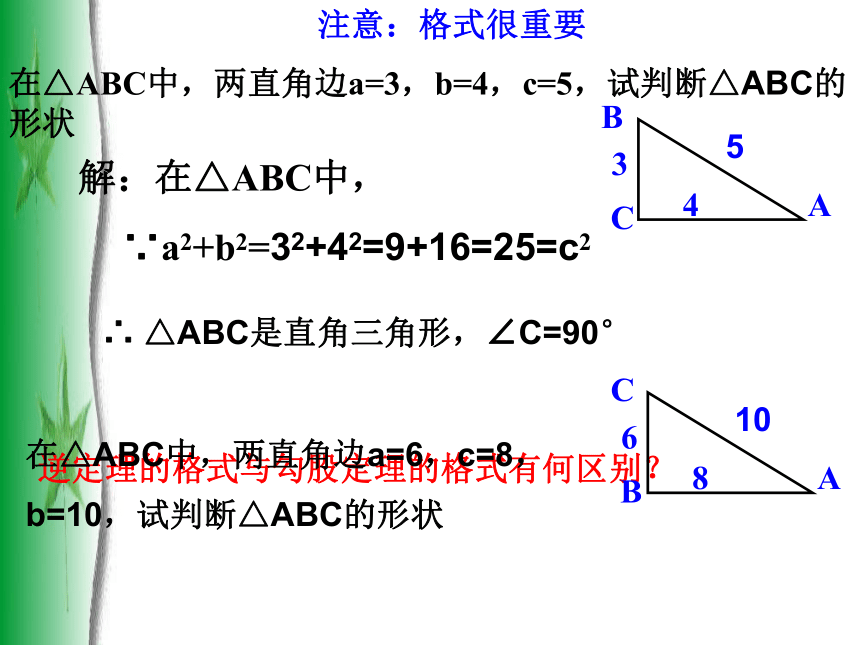
直角三角形。1、哪条边是些斜边？哪个角是直角？2、如果c2+b2=a2 呢，还是直角三角形吗？哪个是直角？知识点1:勾股定理的逆定理3、如果c2-b2=a2 呢，还是直角三角形吗？哪个是直角？注意：格式很重要在△ABC中，两直角边a=3，b=4，c=5，试判断△ABC的形状解：在△ABC中，
∵a2+b2=32+42=9+16=25=c2
逆定理的格式与勾股定理的格式有何区别？在△ABC中，两直角边a=6，c=8，
b=10，试判断△ABC的形状∴ △ABC是直角三角形，∠C=90°例1、一个零件的形状如图1- 11所示，按规定这个零件中，∠A和∠DBC都应为直角，工人师傅量得这个零件各边尺寸如图1- 12所示，这个零件符合要求吗？1- 111- 12例2、一个零件的形状如图1- 11所示， ∠A=90°，按规定这个零件中∠DBC必须为直角，工人师傅量得这个零件各边尺寸如图1- 12所示，这个零件符合要求吗？1- 12满足a2+b2=c2的三个正整数， 称为勾股定理。
常见的基本勾股数有
3，4，5；
5，12，13；
8，15，17；
7，24，25；
9，40，41； 知识点2:勾股数0.3，0.4，0.5是勾股数吗？（以及它们的倍数）P11拓展演练如果将直角三角形的三条边长同时扩大一个相同的倍数，得到的三角形还是直角三角形吗？填写下表，并计算第一列每组数是否为勾股数，她们的2倍、3倍、4倍、10倍呢？9，12，1512，16，2030，40，5010，24，2620，48，5250，120，13016，30，3424，45，5180，150，17014，48，5021，72，7528，96，100请快速计算下列直角三角形的另一边1、如果三角形的三条线段a，b，c满足a2=c2-b2，这个三角形是直角三角形吗？为什么？2、如果三角形的三条线段a，b，c满足以下条件之一，这个三角形是直角三角形吗？为什么？
（1）a=n2-1，b=2n，c=n2+1 （n＞1）
（2）a=m2-n2，b=2mn，c=m2+n2 （m＞n＞0）知识点3:角的比例与边的比例1、满足下列条件的△ABC中,不是直角三角形的是( )
A、b2=c2-a2 B、 ∠C= ∠A- ∠B
C、 a:b:c=3:4:5 D、∠A： ∠B：∠C=5：12：13满足下列条件的△ABC中,哪些是直角三角形？
(1)、 a:b:c=3:4:5 (2)、 ∠A： ∠B： ∠C=3：4：5
(3 )、 a:b:c=1:1:2 (4)、∠A： ∠B：∠C=1：1：2
(5 )、 a:b:c=2:3:5 (6)、∠A： ∠B：∠C=2：3：5随 堂 练 习2、判断下列哪组数是勾股数：
（1）6，7，8； （2）8，15，6；
（3）a=n2-1，b=2n，c=n2+1 （n＞1）
（4）a=m2-n2，b=2mn，c=m2+n2 （m＞n＞0）1、下列几组数能否作为直角三角形的三边长？说说你的理由。
（1）9，12，15； （2）12，18，22；
（3）12，35，36； （4）15，36，39。√√√√例2、一小船先向正南行进了80米到另一小船处借东西，之后又向正东行进了150米，此时它距出发地多少米？解：设它距出发地x米，
在Rt三角形ABC中，
AB2=AC2+BC2
AB2=802+1502=28900=1702，
解得：x=170
此时小船距出发点170米.ACB例3、如图，四边形ABCD中，AB⊥AD，已知AD=3cm，AB=4cm，CD=12cm，BC=13cm，求四边形ABCD 的面积。例3、如图，四边形ABCD中，AB⊥AD，已知AD=3cm，AB=4cm，CD=12cm，BC=13cm，求四边形ABCD 的面积。ACBD4、假期中，王强和同学到某海岛上去探宝旅游，按照探宝图（如图），他们登陆后先往东走8千米，又往北走2千米，遇到障碍后又往西走3千米，再折向北走到6千米处往东一拐，仅走1千米就找到了宝藏，问登陆点A到宝藏埋藏点B的直线距离是多少千米？82361CBC=6+2=8AC=8-3+1=6AB2=AC2+BC2=36+64=100∴ AC=10（千米）古埃及人曾用下面的方法得到直角：他们用13个等距离的结把一根绳子分成等长的12段，一个工匠同时握住第一个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角在第4个结处。3、将一根长为24个单位的绳子，分别标出A，B，C，D四个点，它们将绳子分成长为6个单位、8个单位和10个单位的三条线段，自己握住绳子的两个端点（A点和D点），两名同伴分别握住B点和C点，一起将绳子拉直，会得到一个什么形状的三角形？为什么？因为三边满足勾股定理.