北师大版八年级数学上册第1章勾股定理 知识点分类练习题 难度中等偏上 2022-2023学年(含解析)
文档属性
| 名称 | 北师大版八年级数学上册第1章勾股定理 知识点分类练习题 难度中等偏上 2022-2023学年(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 480.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 16:55:11 | ||
图片预览



文档简介
2022-2023学年北师大版八年级数学上册《第1章勾股定理》知识点分类练习题(附答案)
一.勾股定理
1.在△ABC中,AB=10,AC=17,BC边上的高AD=8,则△ABC的面积为( )
A.72 B.84 C.36 或 84 D.72 或 84
2.有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上“生长”出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图所示的形状图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了888次后形成的图形中所有的正方形的面积和是( )
A.445 B.887 C.888 D.889
3.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.
4.问题背景:在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上.
(2)画△DEF,DE、EF、DF三边的长分别为、、
①判断三角形的形状,说明理由.
②求这个三角形的面积.
二.勾股定理的证明
5.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是:大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式c2=,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题
(1)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.
(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
6.(1)问题情境:
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,借助“数形关系”利用面积法进行证明,而以刘徽的“青朱出入图”为代表的“无字证明”也颇为神奇,证明不需用任何数学符号和文字,整个证明单靠移动几块图形而得出.
如图1和2,将4个全等的直角三角形拼成边长为(a+b)的正方形,使中间留下一个边长为c的空白正方形,画出边长为(a+b)的正方形,再移动三角形至图2所示的位置中,于是留下了边长分别为a和b的两个空白正方形.则图1和图2中的白色部分面积必定相等,即 ;
(2)尝试证明:实际上只需图2的“一半”即可用“数形关系”和面积法证明,美国总统伽菲尔德在1876年利用图3证明了勾股定理,请你来试一试,借助图3完成证明:
(3)问题拓展:已知Rt△ABC的两直角边分别为a,b,斜边为c,求证:≤.
三.勾股定理的逆定理
7.若△ABC的三边a、b、c满足(a﹣b)2+|a2+b2﹣c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
8.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,问过3秒时,△BPQ的面积为多少?
四.勾股数(共2小题)
9.下列各组数据中是勾股数的是( )
A.0.3,0.4,0.5 B.32,42,52
C.9,12,15 D.,,
10.王老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 ……
a 22﹣1 32﹣1 42﹣1 52﹣1 ……
b 4 6 8 10 ……
c 22+1 32+1 42+1 52+1 ……
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n的代数式表示:a= ,b= ,c= .
(2)猜想以a、b、c为边的三角形是否为直角三角形?并证明你的猜想?
(3)观察下列勾股数:32+42=52,52+122=132,72+242=252,92+402=412,分析其中的规律,根据规律写出第五组勾股数.
五.勾股定理的应用
11.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
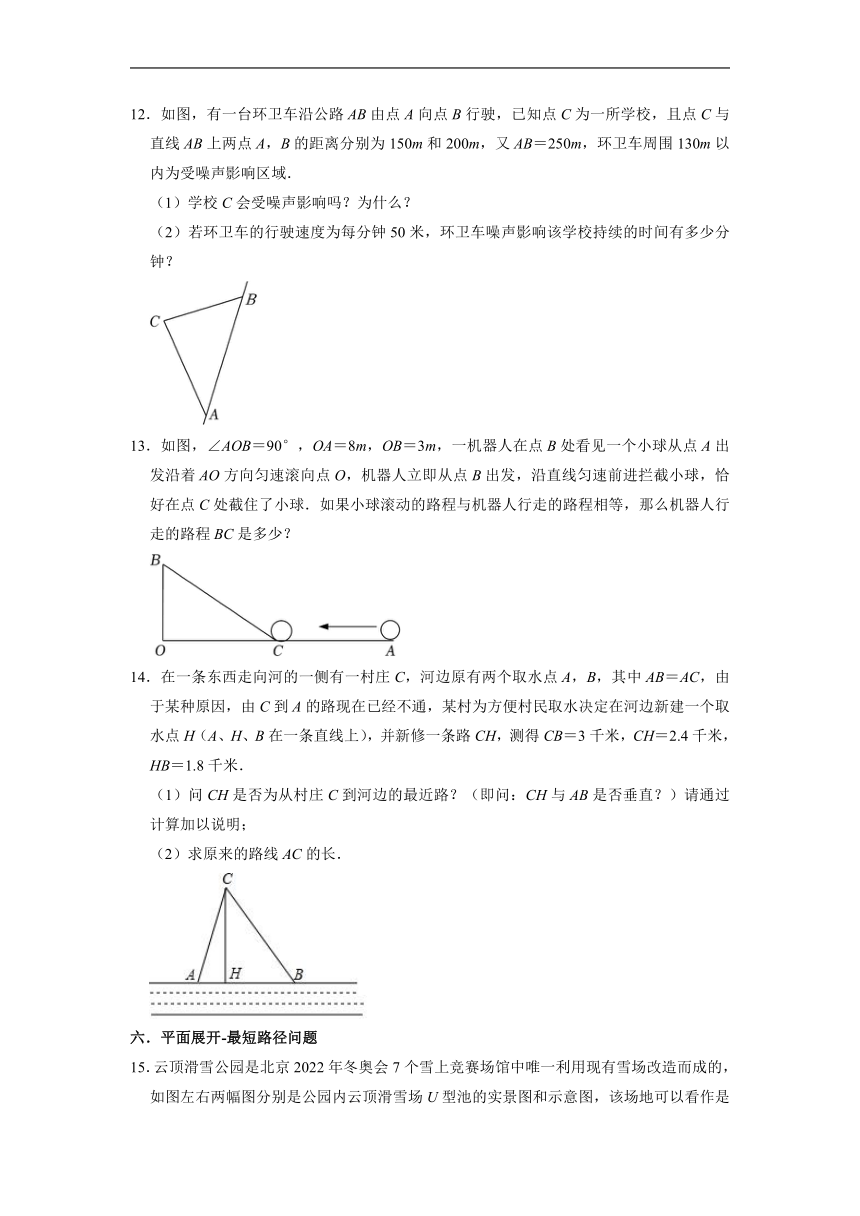
12.如图,有一台环卫车沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,环卫车周围130m以内为受噪声影响区域.
(1)学校C会受噪声影响吗?为什么?
(2)若环卫车的行驶速度为每分钟50米,环卫车噪声影响该学校持续的时间有多少分钟?
13.如图,∠AOB=90°,OA=8m,OB=3m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的路程与机器人行走的路程相等,那么机器人行走的路程BC是多少?
14.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
六.平面展开-最短路径问题
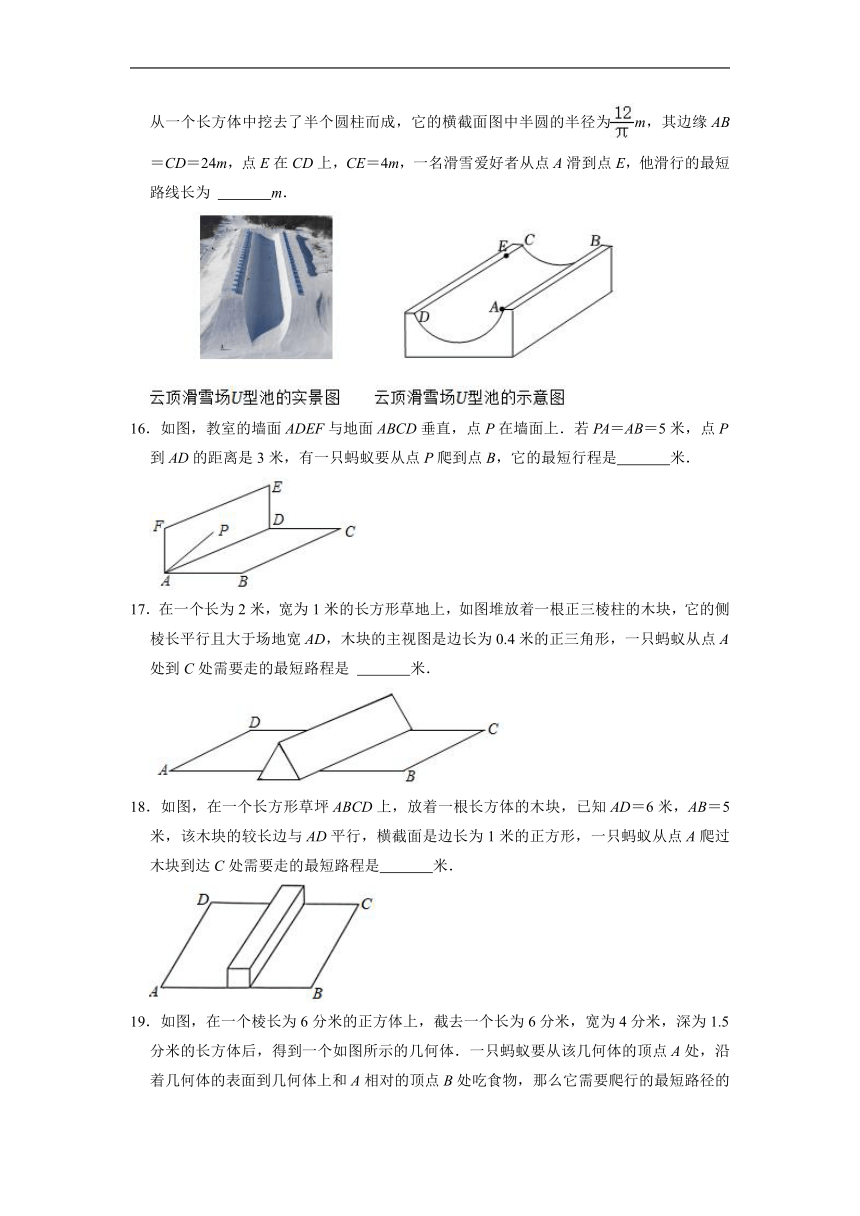
15.云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的,如图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图,该场地可以看作是从一个长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为m,其边缘AB=CD=24m,点E在CD上,CE=4m,一名滑雪爱好者从点A滑到点E,他滑行的最短路线长为 m.
16.如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5米,点P到AD的距离是3米,有一只蚂蚁要从点P爬到点B,它的最短行程是 米.
17.在一个长为2米,宽为1米的长方形草地上,如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽AD,木块的主视图是边长为0.4米的正三角形,一只蚂蚁从点A处到C处需要走的最短路程是 米.
18.如图,在一个长方形草坪ABCD上,放着一根长方体的木块,已知AD=6米,AB=5米,该木块的较长边与AD平行,横截面是边长为1米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是 米.
19.如图,在一个棱长为6分米的正方体上,截去一个长为6分米,宽为4分米,深为1.5分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.
20.如图,一个正方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你在正方体木柜的表面展开图中画出蚂蚁能够最快到达目的地的可能路径;
(2)当正方体木柜的棱长为4时,求蚂蚁爬过的最短路径的长.
21.如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 .
22.仔细阅读,解答下列问题
(1)有一长方体的食物包装纸盒如图(1),已知长方体的底面长为12,宽为9,高为5,一只蚂蚁想从底面A处爬到B处去吃食物,请问:蚂蚁爬行的最短距离是多少?
(2)如图(2),圆柱形容器的高为1.2米,底面周长为1米,在容器内壁离容器底部0.3米的点B处有一只蚊子,此处一只壁虎正好在容器外壁离容器上沿0.3米与蚊子相对的点A处,求壁虎捕捉到蚊子的最短路程是多少?(容器厚度忽略不计).
23.如图.长方体的底面是边长2cm的正方形,高为6cm.如果从点A开始经过4个侧面缠绕2圈到达B,那么所用细线最短需要 cm.
24.华罗庚爷爷说:数学是我国人民所擅长的学科.请同学们求解《九章算术》中的一个古代问题:“今有木长二丈,围之三尺,葛生其下,缠木七周,上与木齐.问葛长几何?”
白话译文:如图,有圆柱形木棍直立地面,高20尺,圆柱底面周长3尺.葛藤生于圆柱底部A点,等距离缠绕圆柱七周,恰好子长到圆柱上底面的B点.问葛藤的长度是多少尺?
参考答案
一.勾股定理
1.解:在Rt△ABD中,由勾股定理得:BD===6,
在Rt△ACD中,由勾股定理得:CD===15,
分两种情况:
①如图1,当AD在△ABC的内部时,BC=15+6=21,
则△ABC的面积=BC×AD=×21×8=84;
②如图2,当AD在△ABC的外部时,BC=15﹣6=9,
则△ABC的面积=BC×AD=×9×8=36;
综上所述,△ABC的面积为36或84,
故选:C.
2.解:根据勾股定理以及正方形的面积公式,可以发现:经过n次生长后,所有正方形的面积和等于第一个正方形的面积的(n+1)倍,
∴生长n次后,变成的图中所有正方形的面积Sn=n+1,
∴生长”了888次后形成的图形中所有的正方形的面积和是888+1=889,
故选:D.
3.解:由折叠可知△ADE和△AFE关于AE成轴对称,
故AF=AD,EF=DE=DC﹣CE=8﹣3=5.
所以CF=4,
设BF=xcm,则AF=AD=BC=x+4.
在Rt△ABF中,由勾股定理,得82+x2=(x+4)2.
解得x=6,故BC=10.
所以阴影部分的面积为:10×8﹣2S△ADE=80﹣50=30(cm2).
4.解:(1)如图,
S△ABC=3×3﹣×3×1﹣×2×1﹣×3×2=3.5;
(2)①△DEF为直角三角形,理由如下:
因为+=,
所以△DEF为直角三角形;
②S△DEF=3×2﹣×3×1﹣×2×2﹣×1×1=2;
答:△DEF的面积为2.
二.勾股定理的证明
5.解:(1)在Rt△ABC中
由面积的两种算法可得:
解得:CD=
(2)在Rt△ABD中AD2=42﹣x2=16﹣x2
在Rt△ADC中AD2=52﹣(6﹣x)2=﹣11+12x﹣x2
所以16﹣x2=﹣11+12x﹣x2…(9分)
解得=(10分)
6.(1)解:在图1中,白色部分为边为c的正方形,其面积为c2,
在图2中,白色部分为边长分别为a和b的两个正方形,其面积和为a2+b2,
而a、b、c是直角三角形的三边,所以有c2=a2+b2,
故答案为:c2=a2+b2;
(2)证明:∵S白三角形=S梯形﹣2S黑三角形,
∴c2=(a+b)(a+b)﹣2×ab,
即c2=a2+b2;
(3)证明:∵0≤(a﹣b)2,
∴2ab≤a2+b2,
∴a2+b2+2ab≤2(a2+b2),
∵a2+b2=c2,
∴(a+b)2≤2c2,
∴≤2,
∴≤.
三.勾股定理的逆定理
7.解:∵(a﹣b)2+|a2+b2﹣c2|=0,
∴a﹣b=0,a2+b2﹣c2=0,
解得:a=b,a2+b2=c2,
∴△ABC的形状为等腰直角三角形;
故选:C.
8.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP BQ=×6×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
四.勾股数
9.解:A、0.3,0.4,0.5都不是正整数,故不是勾股数,不符合题意;
B、92+162≠252,不能构成直角三角形,故不符合题意;
C、92+122=152,三边是整数,同时能构成直角三角形,符合题意;
D、,,都不是整数,故不是勾股数,不符合题意;
故选:C.
10.解:(1)由题意:a=n2﹣1,b=2n,c=n2+1,
故答案为:n2﹣1,2n,n2+1;
(2)猜想:以a、b、c为边的三角形是直角三角形.
理由:∵a=n2﹣1,b=2n,c=n2+1,
∴a2+b2=(n2﹣1)2+4n2=n4+2n2+1=(n2+1)2=c2,
∴以a、b、c为边的三角形是直角三角形.
(3)观察可知:第五组勾股数为:112+602=612.
五.勾股定理的应用
11.解:设水面以下荷叶的高度为OH=hm,则荷叶的高度为AO=BO=(h+1)m,如图所示:
在Rt△OHB中,BH=3m,由勾股定理得:OH2+BH2=BO2,
即h2+32=(h+1)2,
解得:h=4(m),
∴h+1=5(m),
∴荷叶的高度为5m,
故答案为:5m.
12.解:(1)学校C会受噪声影响.
理由:如图,过点C作CD⊥AB于D,
∵AC=150m,BC=200m,AB=250m,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
∴AC×BC=CD×AB,
∴150×200=250×CD,
∴CD==120(m),
∵环卫车周围130m以内为受噪声影响区域,
∴学校C会受噪声影响.
(2)当EC=130m,FC=130m时,正好影响C学校,
∵ED=(m),
∴EF=100(m),
∵环卫车的行驶速度为每分钟50米,
∴100÷50=2(分钟),
即环卫车噪声影响该学校持续的时间有2分钟.
13.解:∵小球滚动的速度与机器人行走的速度相等,
∴BC=AC,
设BC=AC=xm,
则OC=(8﹣x)m,
在Rt△BOC中,
∵OB2+OC2=BC2,
∴32+(8﹣x)2=x2,
解得x=.
∴机器人行走的路程BC为m.
14.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(2.4)2+(1.8)2=9
BC2=9
∴CH2+BH2=BC2
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x﹣1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.8)2+(2.4)2
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
六.平面展开-最短路径问题
15.解:将半圆面展开可得:
AD=12m,DE=DC﹣CE=20m,
在Rt△ADE中,
AE===4(m),
即滑行的最短路线长为4m,
故答案为:4.
16.解:如图,过P作PG⊥BF于G,连接PB,
∵AG=3米,AP=AB=5米,
∴PG=4米,
∴BG=8米,
∴PB==4(米).
故这只蚂蚁的最短行程应该是4米.
故答案为:4.
17.解:如图,将木块展开,得到右图的长方形,
右图长方形的AB相当于是2+0.4+0.4﹣0.4=2.4,
宽仍然为1米.
于是最短路径为:=2.6米.
故答案为:2.6.
18.解:由题意可知,将木块展开,
相当于是AB﹣1+3个正方形的宽,
∴长为5﹣1+3×1=7米;宽为6米.
于是最短路径为:米.
故答案为:
19.解:如图所示,
AB=(分米).
答:它需要爬行的最短路径的长是分米.
故答案为:
20.解:(1)蚂蚁能够最快到达目的地的可能路径有如图的AC′1和AC1.
(2)如上图,AC′1==.AC1==.
所以蚂蚁爬过的最短路径的长是.
21.解:如图:
∵高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,
∴A′D=0.6m,BD=0.8m,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B==
=1(m).
故答案为:1m.
22.解:(1)第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是12cm和14cm,
则所走的最短线段是 =2,
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是9cm和17cm,
所以走的最短线段是=cm;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是21cm和5cm,
所以走的最短线段是=cm;
三种情况比较而言,第一种情况最短,
∴蚂蚁爬行的最短距离是2cm;
(2)如图:∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.5m,BD=1.2m,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=
=
=1.3(m).
答:壁虎捕捉到蚊子的最短路程是1.3m.
23.解:将长方体的侧面沿AB展开,取A′B′的中点C,取AB的中点C′,连接B′C′,AC,则AC+B′C′为所求的最短细线长,
∵AC2=AA′2+A′C2,AC=cm,
∴B′C′2=BB′2+C′B2=73,
∴B′C′=(cm),
∴AC+B′C′=2(cm),
答:所用细线最短长度是2cm,
故答案为:2.
24.解:如图,一条直角边(即木棍的高)长20尺,
另一条直角边长7×3=21(尺),
因此葛藤长=29(尺).
答:葛藤长29尺.
一.勾股定理
1.在△ABC中,AB=10,AC=17,BC边上的高AD=8,则△ABC的面积为( )
A.72 B.84 C.36 或 84 D.72 或 84
2.有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上“生长”出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图所示的形状图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了888次后形成的图形中所有的正方形的面积和是( )
A.445 B.887 C.888 D.889
3.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8cm,求图中阴影部分的面积.
4.问题背景:在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上.
(2)画△DEF,DE、EF、DF三边的长分别为、、
①判断三角形的形状,说明理由.
②求这个三角形的面积.
二.勾股定理的证明
5.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是:大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式c2=,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题
(1)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.
(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
6.(1)问题情境:
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,借助“数形关系”利用面积法进行证明,而以刘徽的“青朱出入图”为代表的“无字证明”也颇为神奇,证明不需用任何数学符号和文字,整个证明单靠移动几块图形而得出.
如图1和2,将4个全等的直角三角形拼成边长为(a+b)的正方形,使中间留下一个边长为c的空白正方形,画出边长为(a+b)的正方形,再移动三角形至图2所示的位置中,于是留下了边长分别为a和b的两个空白正方形.则图1和图2中的白色部分面积必定相等,即 ;
(2)尝试证明:实际上只需图2的“一半”即可用“数形关系”和面积法证明,美国总统伽菲尔德在1876年利用图3证明了勾股定理,请你来试一试,借助图3完成证明:
(3)问题拓展:已知Rt△ABC的两直角边分别为a,b,斜边为c,求证:≤.
三.勾股定理的逆定理
7.若△ABC的三边a、b、c满足(a﹣b)2+|a2+b2﹣c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
8.如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,问过3秒时,△BPQ的面积为多少?
四.勾股数(共2小题)
9.下列各组数据中是勾股数的是( )
A.0.3,0.4,0.5 B.32,42,52
C.9,12,15 D.,,
10.王老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 ……
a 22﹣1 32﹣1 42﹣1 52﹣1 ……
b 4 6 8 10 ……
c 22+1 32+1 42+1 52+1 ……
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n的代数式表示:a= ,b= ,c= .
(2)猜想以a、b、c为边的三角形是否为直角三角形?并证明你的猜想?
(3)观察下列勾股数:32+42=52,52+122=132,72+242=252,92+402=412,分析其中的规律,根据规律写出第五组勾股数.
五.勾股定理的应用
11.如图,一株荷叶高出水面1m,一阵风吹过来,荷叶被风吹的贴着水面,这时它偏离原来位置有3m远,则荷叶原来的高度是 .
12.如图,有一台环卫车沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,环卫车周围130m以内为受噪声影响区域.
(1)学校C会受噪声影响吗?为什么?
(2)若环卫车的行驶速度为每分钟50米,环卫车噪声影响该学校持续的时间有多少分钟?
13.如图,∠AOB=90°,OA=8m,OB=3m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的路程与机器人行走的路程相等,那么机器人行走的路程BC是多少?
14.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
六.平面展开-最短路径问题
15.云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的,如图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图,该场地可以看作是从一个长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为m,其边缘AB=CD=24m,点E在CD上,CE=4m,一名滑雪爱好者从点A滑到点E,他滑行的最短路线长为 m.
16.如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5米,点P到AD的距离是3米,有一只蚂蚁要从点P爬到点B,它的最短行程是 米.
17.在一个长为2米,宽为1米的长方形草地上,如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽AD,木块的主视图是边长为0.4米的正三角形,一只蚂蚁从点A处到C处需要走的最短路程是 米.
18.如图,在一个长方形草坪ABCD上,放着一根长方体的木块,已知AD=6米,AB=5米,该木块的较长边与AD平行,横截面是边长为1米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是 米.
19.如图,在一个棱长为6分米的正方体上,截去一个长为6分米,宽为4分米,深为1.5分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.
20.如图,一个正方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你在正方体木柜的表面展开图中画出蚂蚁能够最快到达目的地的可能路径;
(2)当正方体木柜的棱长为4时,求蚂蚁爬过的最短路径的长.
21.如图,圆柱形容器的高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 .
22.仔细阅读,解答下列问题
(1)有一长方体的食物包装纸盒如图(1),已知长方体的底面长为12,宽为9,高为5,一只蚂蚁想从底面A处爬到B处去吃食物,请问:蚂蚁爬行的最短距离是多少?
(2)如图(2),圆柱形容器的高为1.2米,底面周长为1米,在容器内壁离容器底部0.3米的点B处有一只蚊子,此处一只壁虎正好在容器外壁离容器上沿0.3米与蚊子相对的点A处,求壁虎捕捉到蚊子的最短路程是多少?(容器厚度忽略不计).
23.如图.长方体的底面是边长2cm的正方形,高为6cm.如果从点A开始经过4个侧面缠绕2圈到达B,那么所用细线最短需要 cm.
24.华罗庚爷爷说:数学是我国人民所擅长的学科.请同学们求解《九章算术》中的一个古代问题:“今有木长二丈,围之三尺,葛生其下,缠木七周,上与木齐.问葛长几何?”
白话译文:如图,有圆柱形木棍直立地面,高20尺,圆柱底面周长3尺.葛藤生于圆柱底部A点,等距离缠绕圆柱七周,恰好子长到圆柱上底面的B点.问葛藤的长度是多少尺?
参考答案
一.勾股定理
1.解:在Rt△ABD中,由勾股定理得:BD===6,
在Rt△ACD中,由勾股定理得:CD===15,
分两种情况:
①如图1,当AD在△ABC的内部时,BC=15+6=21,
则△ABC的面积=BC×AD=×21×8=84;
②如图2,当AD在△ABC的外部时,BC=15﹣6=9,
则△ABC的面积=BC×AD=×9×8=36;
综上所述,△ABC的面积为36或84,
故选:C.
2.解:根据勾股定理以及正方形的面积公式,可以发现:经过n次生长后,所有正方形的面积和等于第一个正方形的面积的(n+1)倍,
∴生长n次后,变成的图中所有正方形的面积Sn=n+1,
∴生长”了888次后形成的图形中所有的正方形的面积和是888+1=889,
故选:D.
3.解:由折叠可知△ADE和△AFE关于AE成轴对称,
故AF=AD,EF=DE=DC﹣CE=8﹣3=5.
所以CF=4,
设BF=xcm,则AF=AD=BC=x+4.
在Rt△ABF中,由勾股定理,得82+x2=(x+4)2.
解得x=6,故BC=10.
所以阴影部分的面积为:10×8﹣2S△ADE=80﹣50=30(cm2).
4.解:(1)如图,
S△ABC=3×3﹣×3×1﹣×2×1﹣×3×2=3.5;
(2)①△DEF为直角三角形,理由如下:
因为+=,
所以△DEF为直角三角形;
②S△DEF=3×2﹣×3×1﹣×2×2﹣×1×1=2;
答:△DEF的面积为2.
二.勾股定理的证明
5.解:(1)在Rt△ABC中
由面积的两种算法可得:
解得:CD=
(2)在Rt△ABD中AD2=42﹣x2=16﹣x2
在Rt△ADC中AD2=52﹣(6﹣x)2=﹣11+12x﹣x2
所以16﹣x2=﹣11+12x﹣x2…(9分)
解得=(10分)
6.(1)解:在图1中,白色部分为边为c的正方形,其面积为c2,
在图2中,白色部分为边长分别为a和b的两个正方形,其面积和为a2+b2,
而a、b、c是直角三角形的三边,所以有c2=a2+b2,
故答案为:c2=a2+b2;
(2)证明:∵S白三角形=S梯形﹣2S黑三角形,
∴c2=(a+b)(a+b)﹣2×ab,
即c2=a2+b2;
(3)证明:∵0≤(a﹣b)2,
∴2ab≤a2+b2,
∴a2+b2+2ab≤2(a2+b2),
∵a2+b2=c2,
∴(a+b)2≤2c2,
∴≤2,
∴≤.
三.勾股定理的逆定理
7.解:∵(a﹣b)2+|a2+b2﹣c2|=0,
∴a﹣b=0,a2+b2﹣c2=0,
解得:a=b,a2+b2=c2,
∴△ABC的形状为等腰直角三角形;
故选:C.
8.解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9﹣3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=BP BQ=×6×6=18(cm2).
故过3秒时,△BPQ的面积为18cm2.
四.勾股数
9.解:A、0.3,0.4,0.5都不是正整数,故不是勾股数,不符合题意;
B、92+162≠252,不能构成直角三角形,故不符合题意;
C、92+122=152,三边是整数,同时能构成直角三角形,符合题意;
D、,,都不是整数,故不是勾股数,不符合题意;
故选:C.
10.解:(1)由题意:a=n2﹣1,b=2n,c=n2+1,
故答案为:n2﹣1,2n,n2+1;
(2)猜想:以a、b、c为边的三角形是直角三角形.
理由:∵a=n2﹣1,b=2n,c=n2+1,
∴a2+b2=(n2﹣1)2+4n2=n4+2n2+1=(n2+1)2=c2,
∴以a、b、c为边的三角形是直角三角形.
(3)观察可知:第五组勾股数为:112+602=612.
五.勾股定理的应用
11.解:设水面以下荷叶的高度为OH=hm,则荷叶的高度为AO=BO=(h+1)m,如图所示:
在Rt△OHB中,BH=3m,由勾股定理得:OH2+BH2=BO2,
即h2+32=(h+1)2,
解得:h=4(m),
∴h+1=5(m),
∴荷叶的高度为5m,
故答案为:5m.
12.解:(1)学校C会受噪声影响.
理由:如图,过点C作CD⊥AB于D,
∵AC=150m,BC=200m,AB=250m,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
∴AC×BC=CD×AB,
∴150×200=250×CD,
∴CD==120(m),
∵环卫车周围130m以内为受噪声影响区域,
∴学校C会受噪声影响.
(2)当EC=130m,FC=130m时,正好影响C学校,
∵ED=(m),
∴EF=100(m),
∵环卫车的行驶速度为每分钟50米,
∴100÷50=2(分钟),
即环卫车噪声影响该学校持续的时间有2分钟.
13.解:∵小球滚动的速度与机器人行走的速度相等,
∴BC=AC,
设BC=AC=xm,
则OC=(8﹣x)m,
在Rt△BOC中,
∵OB2+OC2=BC2,
∴32+(8﹣x)2=x2,
解得x=.
∴机器人行走的路程BC为m.
14.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(2.4)2+(1.8)2=9
BC2=9
∴CH2+BH2=BC2
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x﹣1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.8)2+(2.4)2
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
六.平面展开-最短路径问题
15.解:将半圆面展开可得:
AD=12m,DE=DC﹣CE=20m,
在Rt△ADE中,
AE===4(m),
即滑行的最短路线长为4m,
故答案为:4.
16.解:如图,过P作PG⊥BF于G,连接PB,
∵AG=3米,AP=AB=5米,
∴PG=4米,
∴BG=8米,
∴PB==4(米).
故这只蚂蚁的最短行程应该是4米.
故答案为:4.
17.解:如图,将木块展开,得到右图的长方形,
右图长方形的AB相当于是2+0.4+0.4﹣0.4=2.4,
宽仍然为1米.
于是最短路径为:=2.6米.
故答案为:2.6.
18.解:由题意可知,将木块展开,
相当于是AB﹣1+3个正方形的宽,
∴长为5﹣1+3×1=7米;宽为6米.
于是最短路径为:米.
故答案为:
19.解:如图所示,
AB=(分米).
答:它需要爬行的最短路径的长是分米.
故答案为:
20.解:(1)蚂蚁能够最快到达目的地的可能路径有如图的AC′1和AC1.
(2)如上图,AC′1==.AC1==.
所以蚂蚁爬过的最短路径的长是.
21.解:如图:
∵高为0.9m,底面周长为1.2m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.2m与蚊子相对的点A处,
∴A′D=0.6m,BD=0.8m,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B==
=1(m).
故答案为:1m.
22.解:(1)第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是12cm和14cm,
则所走的最短线段是 =2,
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是9cm和17cm,
所以走的最短线段是=cm;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是21cm和5cm,
所以走的最短线段是=cm;
三种情况比较而言,第一种情况最短,
∴蚂蚁爬行的最短距离是2cm;
(2)如图:∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.5m,BD=1.2m,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=
=
=1.3(m).
答:壁虎捕捉到蚊子的最短路程是1.3m.
23.解:将长方体的侧面沿AB展开,取A′B′的中点C,取AB的中点C′,连接B′C′,AC,则AC+B′C′为所求的最短细线长,
∵AC2=AA′2+A′C2,AC=cm,
∴B′C′2=BB′2+C′B2=73,
∴B′C′=(cm),
∴AC+B′C′=2(cm),
答:所用细线最短长度是2cm,
故答案为:2.
24.解:如图,一条直角边(即木棍的高)长20尺,
另一条直角边长7×3=21(尺),
因此葛藤长=29(尺).
答:葛藤长29尺.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
