探索轴对称的性质1[下学期]

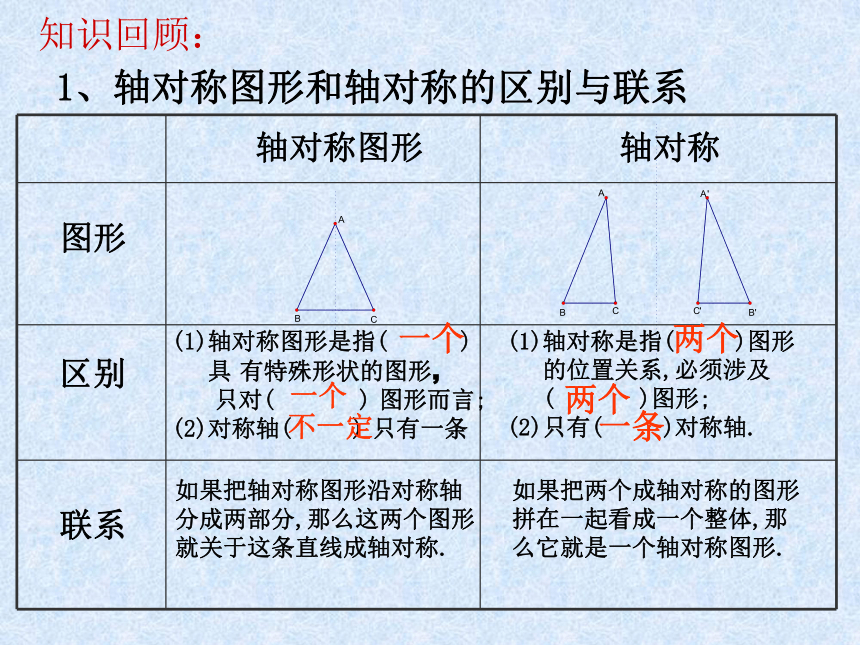
课件32张PPT。 20世纪著名数学家赫尔曼·外 尔所说的，“对称是一种思想，人们毕生追求，并创造次序、美丽和完善……” 探索轴对称的性质1、轴对称图形和轴对称的区别与联系 轴对称图形轴对称 区别联系图形 (1)轴对称图形是指( )
具 有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.一个一个不一定 两个两个一条知识回顾：实物 欣赏蝴蝶建筑 如图7-5，将一张矩形纸对折，然后用笔尖扎出“14’’这个数字，将纸打开后铺平．
(1)上图中，两个“14‘’有什么关
　系?
(2)在上面扎字的过程中，点E　与点E’重合，点F与点F’ 重　合．设折痕所在直线为L，连　接；点E与点E’ 的线段与L有　什么关系?点F与点F’呢?
(3)线段AB与线段A’B’有什么关　系?CD与C’D’呢?
(4)∠1与∠2有什么关系?∠3与　∠4呢?说说你的理由．
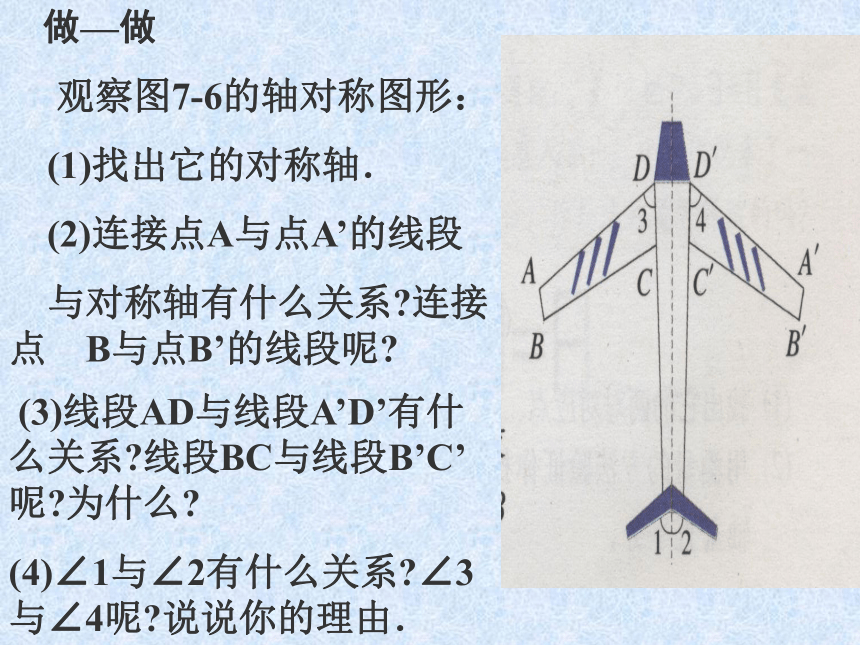
　做—做
　 观察图7-6的轴对称图形：
　(1)找出它的对称轴．
(2)连接点A与点A’的线段
　与对称轴有什么关系?连接　点　B与点B’的线段呢? (3)线段AD与线段A’D’有什么关系?线段BC与线段B’C’呢?为什么?
(4)∠1与∠2有什么关系?∠3与∠4呢?说说你的理由． 在图7—6中，沿对称轴对折后，点A与点A’重合，称
点A关于对称轴的对应点是点A’．类似地，线段AD关于对称轴的对应线段是线段A’D’，∠3关于对称轴的对应角是∠ 4．
对应点所连的线段被对称轴垂直平分。 对应线段相等，对应角相等． 2、△ABC与△DEF关于直线L成轴对称，则∠C是多少度？ L小结：1．轴对称是 图形关于某条直线对称。
轴对称图形是 图形关于某条直线 对称。3．如何把实际问题抽象或转化为几何模型。两个一个2.轴对称的性质：(1).对应点连线段被对称轴垂直平分 (2).对应线段相等，对应角相等。 练习：
1、用笔尖扎重叠的纸可以得到下面　成轴对称的两个图案 (第1题)

(1)找出它的两对对应点、两条对应线　段和两　个对应角．
(2)用测量的方法验证你找到的对应点　所连线　段分别被对称轴垂直平分．2、在下列图形中，找出轴对称图形，并找出　它的两组对应点。3、下图是在方格纸上画出的一棵树的一半，　以树干为对称轴画出树的另一半。观察与思考
1、国旗是一个国家的象征，观察下面的国旗，是轴对称图形的是（ ）
A.加拿大、韩国、乌拉圭 B.加拿大、瑞典、澳大利亚
C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士

加拿大 韩国 澳大利亚 乌拉圭 瑞典 瑞士C 1、 一个角的角平分线就是这个角的对称轴.( )辨析与思考判断× 2、 直线BD是长方形ABCD的对称轴.( )×一个汽车车牌在水中的倒影如图所示，你能确定该车的牌照号码吗？再试牛刀一次晚会上，主持人出了一道题目：“如何把 2+3=8 变成一个真正的等式？”过了很长时间，也没有人答出。小兰仅仅拿了一面镜子，就很快解决了这道题目。你知道她是怎样做的吗？你知道为什么吗？你的眼力下面哪一面镜子里是他的像？（ D ）比一比A′ 如图，EFGH是矩形的台球桌面，有两球分别位于A、B两点的位置，试问怎样撞击A球，才能使A球先碰撞台边EF反弹后再击中B球？试一试：解：1．作点A关于EF的对称点A′ 2．连结A′B交EF于点C则沿AC撞击黑球A，必沿CB反弹击中白球B。C 如果在黑板上写出如下时间，那么镜子里出现的是几点 ? 我来试试看 MN是AB的垂直平分线，EF是BC垂直平分线。PA与PC是否相等，为什么？M动动脑筋 如图，古罗马有一位将军，他每天都要从驻地A 出发，到河边饮马，再到河岸同侧的军营B 巡视。他经常想因该怎样走才能使路程最短，但他百思不得其解。 B′CA
如图，七（1）班与七（2）班两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使PM=PN，请你用折纸的方法找出P点并说明理由。?
BCMN··P1、① 如图, AB//CD,∠ACD的角平分线交AB与E,想一想△ACE是什么三角形. 应用与解释 作业：
课本第232页习题2。