河南省灵宝市第三高级中学2014届高三上学期第一次质量检测数学(文)试题
文档属性
| 名称 | 河南省灵宝市第三高级中学2014届高三上学期第一次质量检测数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 186.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-17 17:42:16 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
灵宝市第三高级中学2014届高三上学期第一次质量检测
数学文试题
一 选择题:(每小题5分,共12道小题,60分)
1.已知集合,则 ( )
A. B.
C. D.
2.已知是虚数单位,则满足的复数为 ( )
A. B. C. D.
3.对于两条直线a,b和平面,若的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分又不必要条件
4.要得到的图象,只要把的图象 ( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
5.下列函数中,既是偶函数又在(0,+∞)单调递增的函数是 ( )
A. B. C. D.
6.命题 p:,使得,命题q: .则下列命题中真命题为( )
A. B.
C. D.
7.在下列区间中函数的零点所在的区间为( )
A. B. C. D.
8.设a,b是两个不共线向量,若共线,则实数k的值为( )
A. B.- C.± D.8
9..定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x∈[0,]时,f(x)=sinx,则f()的值为( )
A.- B. C.- D.
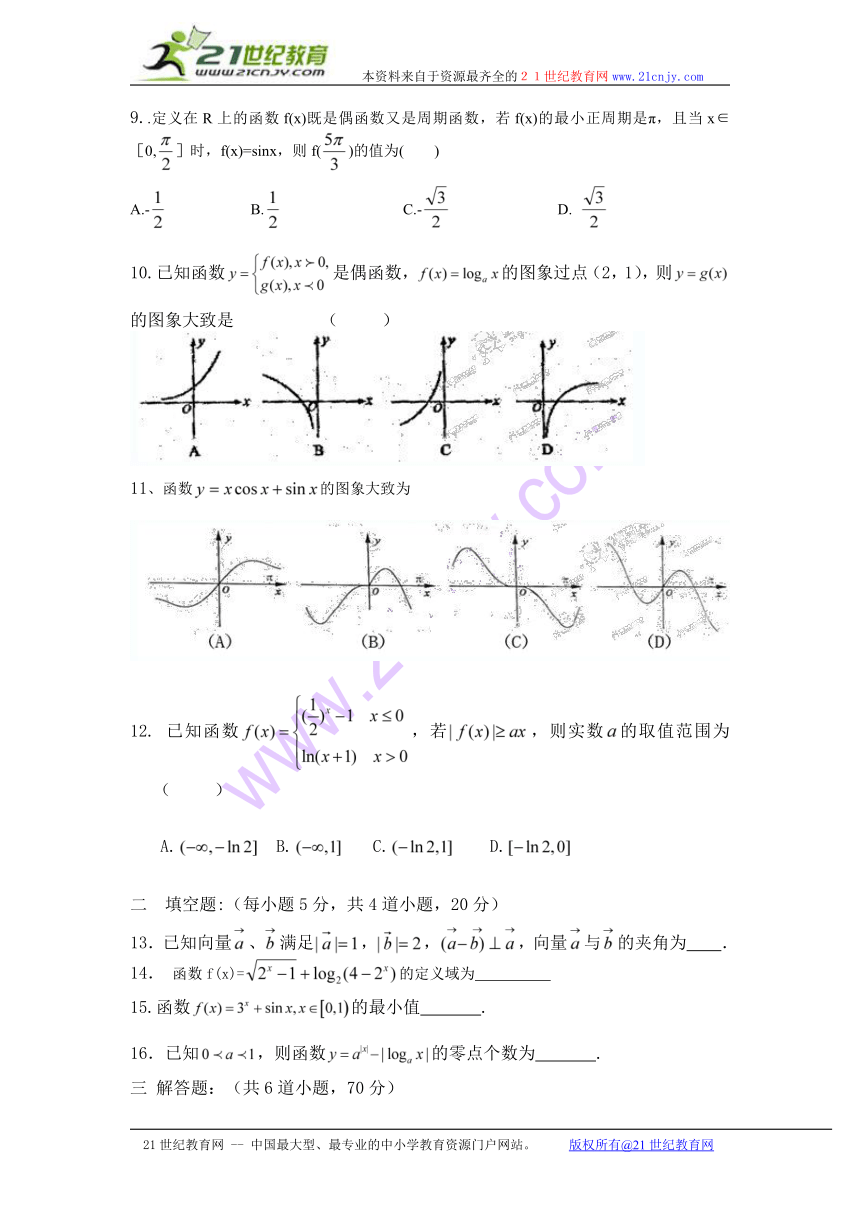
10.已知函数是偶函数,的图象过点(2,1),则的图象大致是 ( )
11、函数的图象大致为
12. 已知函数,若,则实数的取值范围为( )
A. B. C. D.
二 填空题:(每小题5分,共4道小题,20分)
13.已知向量、满足,,,向量与的夹角为 .
14. 函数f(x)=的定义域为
15.函数的最小值 .
16.已知,则函数的零点个数为 .
三 解答题:(共6道小题,70分)
17.(本小题满分10分)已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明.
18.(本小题满分12分)已知集合
(1)若a=1,求;
(2)若是的充分条件,求实数a的取值范围.
19.(本小题满分12分)已知.
(1)化简f(a);
(2)若是第三象限角,且,求f(a)的值.
20.(本小题满分12分)已知函数.(1)求实数的范围,使在区间上是单调递增函数。(2)求的最小值。
21.(本小题满分12分)命题P:关于x的不等式,对一切恒成立,命题q:函数是增函数,若为真,为假,求实数a的取值范围.
22. (本小题满分12分)已知函数
(1)求函数的图像在处的切线方程;
(2)求的最大值;
(3)设实数,求函数在上的最小值.
灵宝三高第一次质量检测高三数学(文科)试题 答案
17.解(1)f(x)=loga(x+1)-loga(1-x),则解得-1(2)由(1)知f(x)的定义域为{x|-1且f(-x)=loga(-x+1)-loga(1+x)
=-[loga(x+1)-loga(1-x)]=-f(x),
故f(x)为奇函数.
18.解:(1)
当a=1时,
则…………6分
(2)
(3)是的充分条件,
即实数a的取值范围是
20.解:(1)因为是开口向上的二次函数,且对称轴为,为了使在上是增函数,故,即 (5分)
(2)当,即时,在上是增函数,所以
当,即时,在上是减函数,在上是增函数,所以
当,即时,在上是减函数,所以
综上可得
22.解析(1)定义域为(0,+∞),
函数处的切线方程为
(2)令 当时, f(x)在(0, e)上为增函数;
当时,在(e,+∞)上为减函数,
(3)∵a>0,由(2)知:F(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
F(x)在[a,2 a]上的最小值
当时,
当2<a时,……14分
(3)另法:①2 a<e,即……8分
②即
1° 时……10分 2°,时,……12分
③时,……13分
时 时,……14分
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
灵宝市第三高级中学2014届高三上学期第一次质量检测
数学文试题
一 选择题:(每小题5分,共12道小题,60分)
1.已知集合,则 ( )
A. B.
C. D.
2.已知是虚数单位,则满足的复数为 ( )
A. B. C. D.
3.对于两条直线a,b和平面,若的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分又不必要条件
4.要得到的图象,只要把的图象 ( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
5.下列函数中,既是偶函数又在(0,+∞)单调递增的函数是 ( )
A. B. C. D.
6.命题 p:,使得,命题q: .则下列命题中真命题为( )
A. B.
C. D.
7.在下列区间中函数的零点所在的区间为( )
A. B. C. D.
8.设a,b是两个不共线向量,若共线,则实数k的值为( )
A. B.- C.± D.8
9..定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x∈[0,]时,f(x)=sinx,则f()的值为( )
A.- B. C.- D.
10.已知函数是偶函数,的图象过点(2,1),则的图象大致是 ( )
11、函数的图象大致为
12. 已知函数,若,则实数的取值范围为( )
A. B. C. D.
二 填空题:(每小题5分,共4道小题,20分)
13.已知向量、满足,,,向量与的夹角为 .
14. 函数f(x)=的定义域为
15.函数的最小值 .
16.已知,则函数的零点个数为 .
三 解答题:(共6道小题,70分)
17.(本小题满分10分)已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明.
18.(本小题满分12分)已知集合
(1)若a=1,求;
(2)若是的充分条件,求实数a的取值范围.
19.(本小题满分12分)已知.
(1)化简f(a);
(2)若是第三象限角,且,求f(a)的值.
20.(本小题满分12分)已知函数.(1)求实数的范围,使在区间上是单调递增函数。(2)求的最小值。
21.(本小题满分12分)命题P:关于x的不等式,对一切恒成立,命题q:函数是增函数,若为真,为假,求实数a的取值范围.
22. (本小题满分12分)已知函数
(1)求函数的图像在处的切线方程;
(2)求的最大值;
(3)设实数,求函数在上的最小值.
灵宝三高第一次质量检测高三数学(文科)试题 答案
17.解(1)f(x)=loga(x+1)-loga(1-x),则解得-1
=-[loga(x+1)-loga(1-x)]=-f(x),
故f(x)为奇函数.
18.解:(1)
当a=1时,
则…………6分
(2)
(3)是的充分条件,
即实数a的取值范围是
20.解:(1)因为是开口向上的二次函数,且对称轴为,为了使在上是增函数,故,即 (5分)
(2)当,即时,在上是增函数,所以
当,即时,在上是减函数,在上是增函数,所以
当,即时,在上是减函数,所以
综上可得
22.解析(1)定义域为(0,+∞),
函数处的切线方程为
(2)令 当时, f(x)在(0, e)上为增函数;
当时,在(e,+∞)上为减函数,
(3)∵a>0,由(2)知:F(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
F(x)在[a,2 a]上的最小值
当时,
当2<a时,……14分
(3)另法:①2 a<e,即……8分
②即
1° 时……10分 2°,时,……12分
③时,……13分
时 时,……14分
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
