2.1 整式 第3课时(多项式) 课件(共15张PPT)
文档属性
| 名称 | 2.1 整式 第3课时(多项式) 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 20:06:01 | ||
图片预览






文档简介
(共15张PPT)
多项式
|2.1 整式 第 3 课时|
2.1 整 式 第2课时 用字母表示数
理解多项式、多项式的项和次数、整式的概念.
会用多项式表示简单的数量关系,并根据多项式中字母的值求多项式的值.
经历用整式表示数量关系的过程,体会用整式表示数量关系的简洁性和一般性.
知识回顾
数或字母的积,单独的一个数或字母也是单项式
单项式的定义:
单项式的系数:
单项式的次数:
单项式中的数字因数
一个单项式中,所有字母的指数的和
的系数是 ____,它的次数是____.
的系数是 ____,它的次数是____.
2
4
新知探究
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
3.如图 (图中长度单位:cm),用式子表示三角尺的面积;
(3x+5y+2z)
(t-5)
问题1 填空
问题2 它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
3x+5y+2z
x2+2x+18
t-5
多项式的定义:几个单项式的和叫做多项式
归纳知识
针对练习
1.下列各式中是多项式的有__________;
①-5a
④π
②
③
⑤
⑥
②③⑤
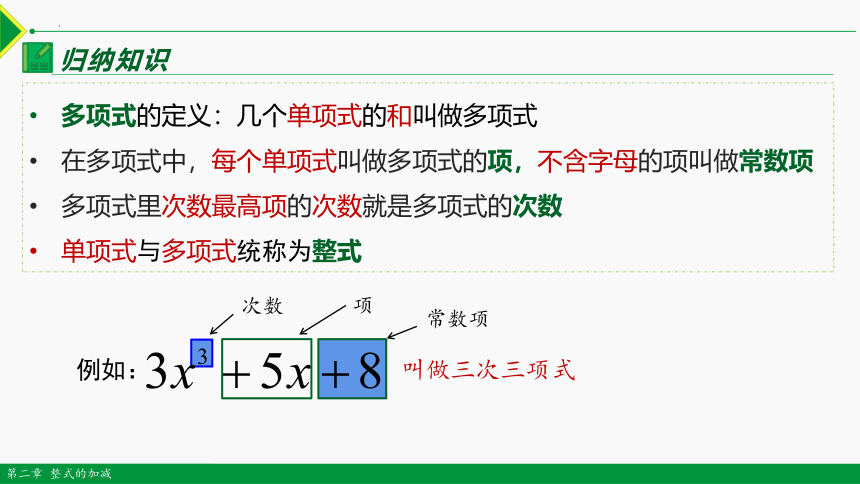
例如:
常数项
次数
项
叫做三次三项式
多项式的定义:几个单项式的和叫做多项式
在多项式中,每个单项式叫做多项式的项,不含字母的项叫做常数项
多项式里次数最高项的次数就是多项式的次数
单项式与多项式统称为整式
归纳知识
典例讲解
例1 指出下列多项式的项和次数,并说明它们是几次几项式?
(1) x4-x2-1;
(2) -3a2-3b2+1;
(3) -2x6+xy-x2y5-2xy3+1.
解:(1) x4-x2-1的项是x4,-x2,-1,次数是4,是四次三项式;
(2) -3a2-3b2+1的项是-3a2,-3b2,1,次数是2,是二次三项式;
(3) -2x6+x5y2-x2y5-2xy3+1的项是-2x6,x5y2,-x2y5,-2xy3,1,次数是7,是七次五项式.
例2 已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,
所以m=4.
所以该多项式为-5x4+104x5-4x4y2.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
例3 若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得
m=0,n-1=0,
所以n=1.
课堂小结
次数 : 所有字母的指数的和
系数:单项式中的数字因数
次数:多项式中次数最高的项的次数
项:式中的每个单项式叫多项式的项,
(其中不含字母的项叫做常数项)
整式
单项式
多项式
随堂练习
1. 将式子: 填入相应的大括号中.
单项式:{ ,…};
多项式:{ ,…};
整式:{ ,…}.
2.一个关于字母x的二次三项式的二次项系数为4,一次项系数为1,常数项为7,则这个二次三项式为_____.
4x2+x+7
3.若 是关于x的一次式,则a =______,若它是关于x的二次二项式,则a =______.
4.多项式 是关于a、b的四次三项式,且最高次项的系数为-2,则x=______,y=______.
2
-3
-5
3
5.下列多项式各有几项?每项次数是什么?是几次几项式?
(1)5-x3y4+x2y2; (2) .
解:(1)5-x3y4+x2y2的项有5,-x3y4,+x2y2,其中5是常数项,-x3y4次数是7,+x2y2次数是4,它是七次三项式;
(2 ) 的项有 , , , , 其中
是常数项 , 次数是3, 次数是2, 次数是1, 它是三次四项式.
6. 某公园的门票价格如下:成人票每张20元,学生票每张10元.一个旅游团有a个成人,b个学生.(1)该旅游团应付门票多少元?(2)若该旅游团有30个成人,10个学生,则他们应付门票多少元?
解:(1)该旅游团应付的门票费是(20a+10b)元.
(2)把a=30,b=10代入代数式,得
20a+10b =20×30+10×10 =700.
因此,他们应付700元门票费
多项式
|2.1 整式 第 3 课时|
2.1 整 式 第2课时 用字母表示数
理解多项式、多项式的项和次数、整式的概念.
会用多项式表示简单的数量关系,并根据多项式中字母的值求多项式的值.
经历用整式表示数量关系的过程,体会用整式表示数量关系的简洁性和一般性.
知识回顾
数或字母的积,单独的一个数或字母也是单项式
单项式的定义:
单项式的系数:
单项式的次数:
单项式中的数字因数
一个单项式中,所有字母的指数的和
的系数是 ____,它的次数是____.
的系数是 ____,它的次数是____.
2
4
新知探究
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
3.如图 (图中长度单位:cm),用式子表示三角尺的面积;
(3x+5y+2z)
(t-5)
问题1 填空
问题2 它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
3x+5y+2z
x2+2x+18
t-5
多项式的定义:几个单项式的和叫做多项式
归纳知识
针对练习
1.下列各式中是多项式的有__________;
①-5a
④π
②
③
⑤
⑥
②③⑤
例如:
常数项
次数
项
叫做三次三项式
多项式的定义:几个单项式的和叫做多项式
在多项式中,每个单项式叫做多项式的项,不含字母的项叫做常数项
多项式里次数最高项的次数就是多项式的次数
单项式与多项式统称为整式
归纳知识
典例讲解
例1 指出下列多项式的项和次数,并说明它们是几次几项式?
(1) x4-x2-1;
(2) -3a2-3b2+1;
(3) -2x6+xy-x2y5-2xy3+1.
解:(1) x4-x2-1的项是x4,-x2,-1,次数是4,是四次三项式;
(2) -3a2-3b2+1的项是-3a2,-3b2,1,次数是2,是二次三项式;
(3) -2x6+x5y2-x2y5-2xy3+1的项是-2x6,x5y2,-x2y5,-2xy3,1,次数是7,是七次五项式.
例2 已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,
所以m=4.
所以该多项式为-5x4+104x5-4x4y2.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
例3 若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
分析:多项式不含哪一项,则哪一项的系数为0.
解:由题意得
m=0,n-1=0,
所以n=1.
课堂小结
次数 : 所有字母的指数的和
系数:单项式中的数字因数
次数:多项式中次数最高的项的次数
项:式中的每个单项式叫多项式的项,
(其中不含字母的项叫做常数项)
整式
单项式
多项式
随堂练习
1. 将式子: 填入相应的大括号中.
单项式:{ ,…};
多项式:{ ,…};
整式:{ ,…}.
2.一个关于字母x的二次三项式的二次项系数为4,一次项系数为1,常数项为7,则这个二次三项式为_____.
4x2+x+7
3.若 是关于x的一次式,则a =______,若它是关于x的二次二项式,则a =______.
4.多项式 是关于a、b的四次三项式,且最高次项的系数为-2,则x=______,y=______.
2
-3
-5
3
5.下列多项式各有几项?每项次数是什么?是几次几项式?
(1)5-x3y4+x2y2; (2) .
解:(1)5-x3y4+x2y2的项有5,-x3y4,+x2y2,其中5是常数项,-x3y4次数是7,+x2y2次数是4,它是七次三项式;
(2 ) 的项有 , , , , 其中
是常数项 , 次数是3, 次数是2, 次数是1, 它是三次四项式.
6. 某公园的门票价格如下:成人票每张20元,学生票每张10元.一个旅游团有a个成人,b个学生.(1)该旅游团应付门票多少元?(2)若该旅游团有30个成人,10个学生,则他们应付门票多少元?
解:(1)该旅游团应付的门票费是(20a+10b)元.
(2)把a=30,b=10代入代数式,得
20a+10b =20×30+10×10 =700.
因此,他们应付700元门票费
