第二章 整式复习 第1课时 课件(共14张PPT)
文档属性
| 名称 | 第二章 整式复习 第1课时 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 11:22:56 | ||
图片预览






文档简介
(共14张PPT)
2.2 整式复习 第1课时
人教版 七年级上册
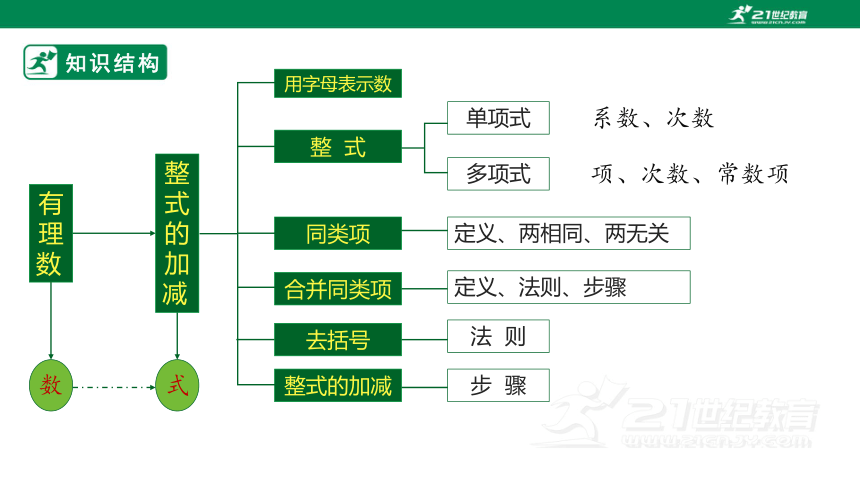
知识结构
整式的加减
用字母表示数
单项式
多项式
去括号
同类项
合并同类项
整式的加减
系数、次数
项、次数、常数项
定义、两相同、两无关
定义、法则、步骤
法 则
步 骤
整 式
有理数
数
式
知识要点
1.单项式:都是数或字母的积,这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式的系数:单项式中的数字因数叫做这个单项式的系数.
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
一、整式的有关概念
4.多项式:几个单项式的和叫做多项式.
5.多项式的次数:多项式里次数最高项的次数,叫做这个多项式的次数.
6.整式:单项式与多项式统称整式.
一、整式的有关概念
1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.几个常数项也是同类项.
2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项,即把它们的系数相加作为新的系数,而字母部分不变.
【注意】
(1)同类项不考虑字母的排列顺序,如-7xy与yx是同类项;
(2)只有同类项才能合并,如x2+x3不能合并.
二、同类项、合并同类项
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项
三、整式的加减
课堂练习
D
C
B
单项式:_______________________;
多项式:________________;
整式:_______________________________________.
5.计算4a+2a-a的结果等于________.
5a
6.下列去括号正确的是( )
A.3a-(2a-c)=3a-2a+c
B.3a+2(2b-3c)=3a+4b-3c
C.6a+(-2b+5)=6a+2b-5
D.(5x-3y)-(2x-y)=5x+3y-2x+y
A
(2)2(2x-3y)-(3x+2y+1),其中x=2,y=- .
8.一名同学做一道题:已知两个多项式A,B,计算2A+B,他误将“2A+B”看成“A+2B”,求得的结果为9x2-2x+7.已知B=x2+3x-2,求2A+B的正确结果.
解:将B=x2+3x-2代入A+2B=9x2-2x+7,得
A+2(x2+3x-2)=9x2-2x+7,
则A=9x2-2x+7-2(x2+3x-2)
=9x2-2x+7-2x2-6x+4
=7x2-8x+11.
将A=7x2-8x+11,B=x2+3x-2代入2A+B,得
2(7x2-8x+11)+(x2+3x-2)
=14x2-16x+22+x2+3x-2
=15x2-13x+20.
所以2A+B的正确结果是:15x2-13x+20.
2.2 整式复习 第1课时
人教版 七年级上册
知识结构
整式的加减
用字母表示数
单项式
多项式
去括号
同类项
合并同类项
整式的加减
系数、次数
项、次数、常数项
定义、两相同、两无关
定义、法则、步骤
法 则
步 骤
整 式
有理数
数
式
知识要点
1.单项式:都是数或字母的积,这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
2.单项式的系数:单项式中的数字因数叫做这个单项式的系数.
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
一、整式的有关概念
4.多项式:几个单项式的和叫做多项式.
5.多项式的次数:多项式里次数最高项的次数,叫做这个多项式的次数.
6.整式:单项式与多项式统称整式.
一、整式的有关概念
1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.几个常数项也是同类项.
2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项,即把它们的系数相加作为新的系数,而字母部分不变.
【注意】
(1)同类项不考虑字母的排列顺序,如-7xy与yx是同类项;
(2)只有同类项才能合并,如x2+x3不能合并.
二、同类项、合并同类项
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项
三、整式的加减
课堂练习
D
C
B
单项式:_______________________;
多项式:________________;
整式:_______________________________________.
5.计算4a+2a-a的结果等于________.
5a
6.下列去括号正确的是( )
A.3a-(2a-c)=3a-2a+c
B.3a+2(2b-3c)=3a+4b-3c
C.6a+(-2b+5)=6a+2b-5
D.(5x-3y)-(2x-y)=5x+3y-2x+y
A
(2)2(2x-3y)-(3x+2y+1),其中x=2,y=- .
8.一名同学做一道题:已知两个多项式A,B,计算2A+B,他误将“2A+B”看成“A+2B”,求得的结果为9x2-2x+7.已知B=x2+3x-2,求2A+B的正确结果.
解:将B=x2+3x-2代入A+2B=9x2-2x+7,得
A+2(x2+3x-2)=9x2-2x+7,
则A=9x2-2x+7-2(x2+3x-2)
=9x2-2x+7-2x2-6x+4
=7x2-8x+11.
将A=7x2-8x+11,B=x2+3x-2代入2A+B,得
2(7x2-8x+11)+(x2+3x-2)
=14x2-16x+22+x2+3x-2
=15x2-13x+20.
所以2A+B的正确结果是:15x2-13x+20.
