第一章 有理数 章节复习课件(共64张PPT)
文档属性
| 名称 | 第一章 有理数 章节复习课件(共64张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览








文档简介
(共64张PPT)
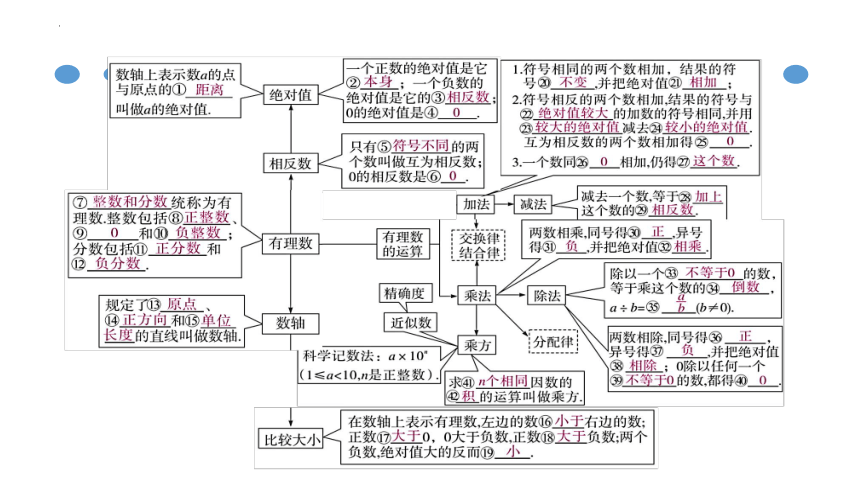
有理数章节复习
1.对本章知识要点进行复习梳理;
2.会运用有理数的运算法则、运算律,熟练进行有理数的运算; (重点、难点)
3.用科学记数法表示绝对值较大的数;
4.用四舍五入法,按要求(精确度)确定运算结果.
4.用正、负数表示具有相反意义的量.
一、正数和负数
1.像1,2,3,1.8%这样大于0的数叫做正数.
2.像-3,-1,-2,-2.7%这样在正数前面加上符号“-”(负)的数叫做负数.
3.0既不是正数,也不是负数.
5.具有相反意义的量应满足的条件:
①必须是同类量,而且是成对出现的;②只要求意义相反,不要求数量一定相等.
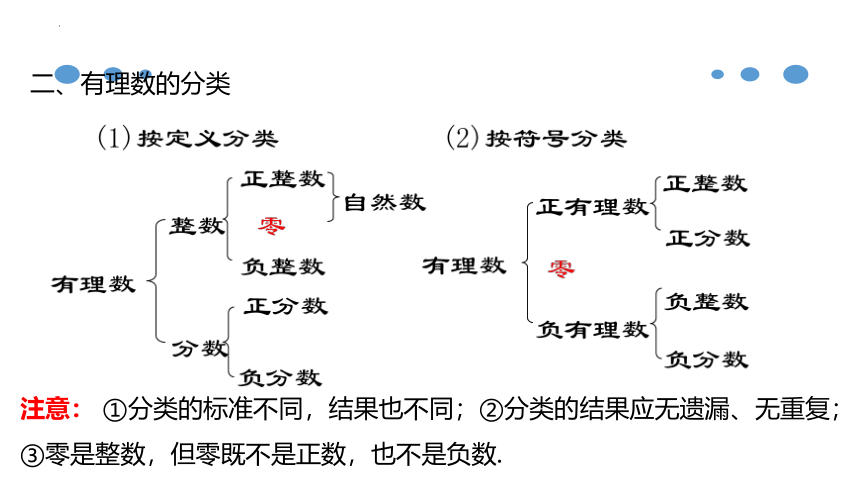
二、有理数的分类
注意: ①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
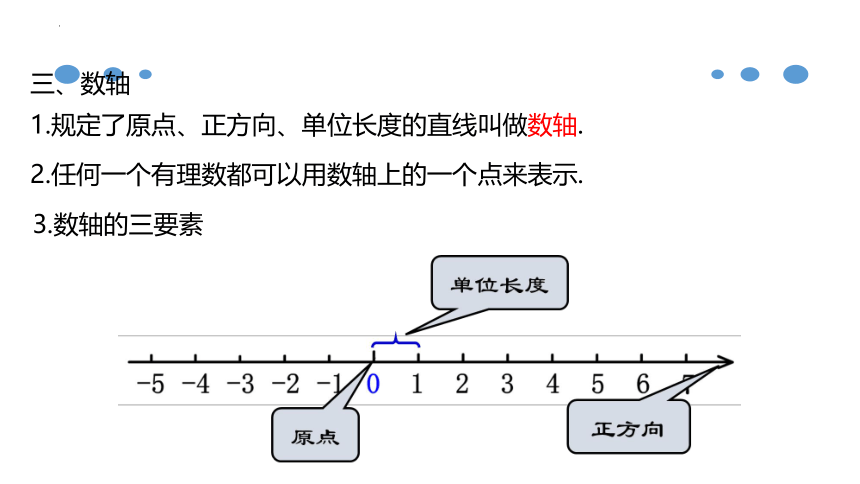
三、数轴
3.数轴的三要素
1.规定了原点、正方向、单位长度的直线叫做数轴.
2.任何一个有理数都可以用数轴上的一个点来表示.
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.(单位长度要一致)
0
0
1
2
3
-1
-2
-3
三、数轴
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻度均匀.
画数轴注意事项:
三、数轴
位置特征:1.分居原点左右;2.到原点距离相等.
a的相反数是-a ; 0的相反数是0
2
5
2
5
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
四、相反数
五、绝对值
1.定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,用“|a|”表示.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
2.绝对值的性质及应用
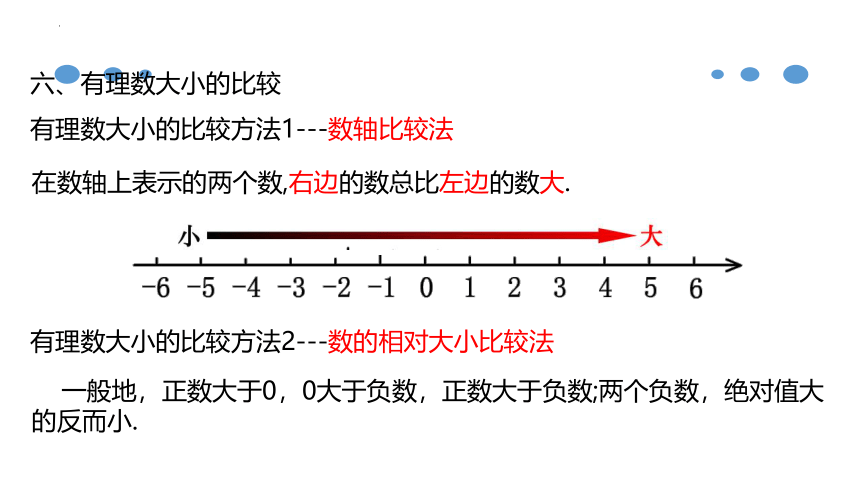
六、有理数大小的比较
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
七、有理数的运算
有理数加法运算的基本解题思路:
1.先判断类型(同号、异号等);2.再确定和的符号;3.最后进行绝对值的加减运算.
七、有理数的运算
(a+b)+c=a+(b+c)
a+b=b+a
1.加法交换律:在有理数加法中,两个数相加,交换加数的位置,和不变.
2.加法结合律:在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
用字母表示为:
用字母表示为:
七、有理数的运算
有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题.
七、有理数的运算
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
七、有理数的运算
法则二:两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0.
法则一:除以一个不等于0的数,等于乘这个数的倒数.
1.有理数除法法则:
2.有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
3.乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
七、有理数的运算
3.乘方的符号法则:
(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数,负数的偶次幂是正数;(3)零的正整数次幂都是零.
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.组成要素
1.乘方的定义
七、有理数的运算
(1)看清运算,定运算顺序;
(2)根据特点,巧用运算律;
(3)选对法则,耐心计算.
2.有理数的加减乘除混合运算三步走:
【运算顺序】1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.有理数的混合运算
我们可以把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10), n是正整数.这种记数方法叫做科学记数法.
1.用科学计数法表示较大的数应注意以下两点:
1≤<10
当大数是大于10的整数时,n为整数位减去1.
2.灵活运用科学计数法,注意解题技巧,总结解题规律.
八、科学记数法
九、近似数
1.近似数:
(1)我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
(2)有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,2022年全国高考报名人数1193万人.
近似数与准确数的接近程度,可以用精确度表示.
2.精确度:
正数和负数的概念及其应用
1
例1.牛奶盒的包装上印有260±5ml,下列四盒送去质检,不合格的是( )
A.265ml B.262ml C.258ml D.250ml
【分析】解:∵牛奶盒的包装上印有260±5ml,
∴最大值为:260+5=265(ml),最小值为:260-5=255(ml),
∴选项A、B、C均合格,选项D不合格.
故选:D.
D
正数和负数的概念及其应用
1
例2.下列是具有相反意义的量是( )
A.身高增加1cm和体重减少1kg B.顺时针旋转90°和逆时针旋转45°
C.向右走2米和向西走5米 D.购买5本图书和借出4本图书
【分析】解:A、身高和体重不是相反的量,不符合题意;
B、顺时针旋转与逆时针旋转是具有相反意义的量,符合题意;
C、向右和向西不是相反的量,不符合题意;
D、购买和借出不是相反的量,不符合题意;
故选:B.
B
正数和负数的概念及其应用
1
例3.北京与柏林的时差为7小时,例如,北京时间14:00,同一时刻的柏林时间是7:00.小丽和小红分别在北京和柏林,她们相约在各自当地时间8:00~17:00之间选择一个时刻开始通话,这个时刻可以是北京时间( )
A.9:30 B.11:30 C.13:30 D.15:30
【分析】解:由题意得,柏林时间比北京时间早7小时,
当柏林时间为8:00,则北京时间为15:00;当北京时间为17:00,则柏林时间为10:00;
所以这个时间可以是北京时间的15:00到17:00之间,
故选:D.
D
【1-1】某运动项目的比赛规定,胜一场记作“+1”分,平局记作“0”分,如果某队得到“-1”分,则该队在比赛中( )
A.与对手打成平局 B.输给对手 C.打赢了对手 D.无法确定
【1-2】下列各组数中,具有相反意义的量是( )
A.盈利40元和运出货物20吨 B.向东走4千米和向南走4千米
C.身高180 cm和身高90cm D.收入500元和支出200元
B
D
城市 悉尼 纽约
时差/时 +2 -13
【1-3】纽约、悉尼与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京晚的时数):
当北京10月1日23时,悉尼、纽约的时间分别是 ( )
A.9月30日21时;9月30日10时 B.10月1日10时;10月2日10时
C.10月2日1时; 10月1日10时 D.9月30日21时;10月2日12时
C
有理数的相关概念、分类及其应用
2
例4. 下列各数中,是负整数的是( )
A.-23 B.-|-0.1| C.-(-) D.(-2)2
A
【分析】解:A.-23=-8,是负整数;
B.-|-0.1|=-0.1,是负分数不是负整数;
C.-(-)=,是正分数不是负整数;
D.(-2)2=4,是正整数不是负整数;
故选A.
例5.把下列各数填在相应的集合中:
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
有理数的相关概念、分类及其应用
2
【2-1】下列说法正确的是( )
A.正有理数和负有理数组成全体有理数 B.零既不是正数,也不是负数
C.0.5既不是整数,也不是分数,因而它不是有理数 D.在有理数中,零的意义表示没有
【2-2】在 ,,,,,,, 中,
整数是________;正分数是_____________________;有理数有____个.
B
7
-17,0
,,,
【2-3】指出下列各数中的正数、负数、整数、分数:
-15,+6,-2,-0.9,1,,0,3,0.63,-4.95.
解:正数集合:{ }
负数集合:{ }
整数集合:{ }
分数集合:{ }
-15,-2,-0.9,-4.95,…
-15,+6,-2,1,0,…
-0.9,,3,0.63,-4.95,…
+6,1,3,0.63…
数轴、相反数、绝对值的概念及相关运算
3
例6.如果小虫在数轴上爬行了5个单位长度后停在表示﹣3的点上,那么小虫开始爬行的位置是表示( )的点.
A.﹣8 B.﹣2 C.﹣8或2 D.8或﹣2
C
分析:逆向思维.距离-3的点5个单位长度的点有两个,分别在-3的左边是-8;右边是2.
例7.若 ,则a=____,b=_____.
【解析】一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
解:因为
所以
所以
所以a=-5,b=3.
【点睛】几个非负数的和为0,则这几个数都为0.
3
-5
数轴、相反数、绝对值的概念及相关运算
3
数轴、相反数、绝对值的概念及相关运算
3
例8.点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:(1)b﹣a<0;(2)|a|<|b|;(3)a+b>0;(4)>0.其中正确的是( ) A.(1)(2) B.(2)(3) C.(3)(4) D.(1)(4)
【分析】解:根据图示,可得﹣3<a<0,b>3,
∴(1)b﹣a>0,故错误;(2)|a|<|b|,故正确;(3)a+b>0,故正确;(4)<0,故错误.故选B.
B
数轴、相反数、绝对值的概念及相关运算
3
例9.如果、、是非零有理数,且,那么的所有可能的值为_____.
【分析】、、为非零有理数,且
、、只能为两正一负或一正两负.
①当、、为两正一负时,设、为正,为负
原式
②当、、为一正两负时,设为正,、为负
原式综上,的值为.
0
例10.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索:
(1)计算|5-(-2)|=______;
(2)使得|x-1|+|x+5|=6这样的整数有_______________________(写出所有符合条件的整数);
(3)由以上探索猜想对于任何有理数x,式子|x-2|+|x+3.5|是否有最小值?________
数轴、相反数、绝对值的概念及相关运算
3
数轴、相反数、绝对值的概念及相关运算
3
解:(1),
故答案为:7;
(2)可以理解为:数轴上某点到1所对应的点的距离和到所对应的点的距离之和为6,满足条件的整数有:,,,,,0,1,
故答案为:,,,,,0,1;
(3)有,理解为:数轴上某点到2所对应的点的距离和到所对应的点的距离之和,其最小值为.
【3-1】点A为数轴上表示-1的动点,当点A沿数轴移动3个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-4 C.2或-4 D.不同于以上
C
【3-2】下列各对数中,互为相反数的有( )
①-1与+1;②+(+1)与-1;③-(-2)与+(-2);④-(-)与+(+) ;
⑤+[-(+1)]与-[+(-1)];⑥-(+2)与-(-2).
A.6对 B.5对 C.4对 D.3对
B
【3-3】在数轴上,a,b所表示的数如图所示,下列结论正确的是( )
A.a+b>0 B.|b|<|a| C.a﹣b>0 D.a b>0
C
【3-4】若,则______.
4
【3-5】|x﹣5|+|2﹣x|的最小值为_____.
3
有理数的大小比较
4
例11.比较下列各对数的大小.
(1) -(-1)和-(+2);(2)-和-;(3) -(-0.3)和|-|.
解:(1)先化简,-(-1)=1,-(+2)=-2
因为正数大于负数,
所以1>-2,即 -(-1)>-(+2)
(2)这是两个负数比较大小,先求它们的绝对值.
|-|= ,|-|= =
因为< ,即|-|<|-|,
所以->-
(3)先化简,-(-0.3)=0.3,|-|=
0.3< ,即-(-0.3)<|-|.
有理数的大小比较
4
例12.若、为有理数,,,且,那么,,,的大小关系是( )
A. B.
C. D.
C
【分析】解:∵,,且,
∴,,,
∴,
∴.故选:C.
【4-2】下列判断,正确的是( )
A.若a>b,则│a│>│b│ B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│ D.若a>b>0,则│a│>│b│
D
【4-3】绝对值大于1而不大于4的整数有__________________________.
-4、-3、-2、2、3、4
【4-1】下列四组有理数大小的比较正确的是( )
A.-> B.->- C.->- D.>
D
例13.计算:
(1)2×(-3)3-4×(-3)+15 (2)(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2)
解:(1)原式=2×(-27)-(-12)+15
=-54+12+15
=-27
(2)原式=-8+(-3)×(16+2)-9÷(-2)
=-8+(-3)×18-(-4.5)
=-8-54+4.5
=-57.5
有理数的运算
5
有理数的运算
5
例14.已知a,b互为相反数,c、d互为倒数,x的平方是4.试求x2-(a+b+cd)x
+(a+b)2000+(-cd)2020的值.
解:根据题意得,
a+b=0,cd=1,x2=4(即x=±2)
(1)当x=2时,原式=4-(0+1)×2+02000+(-1)2020=4-2+O+1=3
(2)当x=-2时,原式=4-(0+1)×(-2)+02000+(-1)2020=4-(-2)+O+1=7.
有理数的运算
5
例15.计算:
解:设,,,
而A+B==1,∴原式=.
【5-2】如图是一个计算程序,若输入a的值为-1,则输出的结果应为( )
A.7 B.﹣5 C.1 D.5
【5-1】计算﹣23+[(﹣4)2﹣(1﹣32)×3]= .
B
32
【5-3】现规定一种新的运算“☉”: a☉b=ab,如3☉2=32=9.则3等于( )
A. B.8 C. D.
A
例16.某公司去年1~3月平均每月亏损1.5万元,4~6月平均盈利2万元,7~10月平均盈利1.7万元,11~12月平均亏损2.3万元,这个公司去年总盈亏情况如何?
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为
(-1.5)×3+2×3+1.7×4+(-2.3)×2
=-4.5+6+6.8-4.6
=3.7
答:这个公司去年全年盈利3.7万元.
有理数运算的实际应用
6
有理数运算的实际应用
6
例17.入冬以来,某品牌的羽绒服统计了在西乡市场某一周的销售情况,以每天100件为标准,超过的件数记作正数,不足的件数记作负数,记录如下:8,12,-9,6,-11,10,-2.
(1)求销量最多的一天比销量最少的一天多销售______件;
(2)该品牌羽绒服这一周的销售总量是多少件?若每件羽绒服的利润为130元,则这一周销售该品牌羽绒服的总利润为多少元?
有理数运算的实际应用
6
解:(1)(件)
(2)7×100+8+12+(-9)+6+(-11)+10+(-2)=714(件)
所以该品牌羽绒服这一周的销售总量是714件.
714×130=92820(元)
所以这一周销售该品牌羽绒服的总利润为92820元.
【6-1】某人用400元购买了8套儿童服装,准备以一定价格出售.他以每套55元的价格为标准,将超出的记作正数,不足的记作负数,记录如下:+2,-3,+2,+1,-2,-1,0,-2(单位:元).他卖完这8套儿童服装后是盈利还是亏损?他盈利(或亏损)了多少钱?
解:(元),
(元),
答:他盈利了37元.
【6-2】武汉百步亭小区交警每天都骑摩托车沿南北街来回巡逻,早晨从A地出发,晚上最后到达B地.假定向北为正方向,当天巡逻记录如下(单位:km):14,﹣9,18,﹣7,13,﹣6,10,﹣6,问:
(1)B地在A地什么位置?
(2)若摩托车每千米耗油0.1升,则一共需耗油多少升?
解:(1)14-9+18-7+13-6+10-6=14+18+13+10-9-7-6-6=27(km),
答:B在A正北27km;
(2)|14|+|﹣9|+|18|+|﹣7|+|13|+|﹣6|+|10|+|﹣6|=83(km),
83×0.1=8.3 (升 ),
答:一共需耗油8.3升.
【6-3】2021年国庆档电影《长津湖》以抗美援朝为背景,讲述了中国人民志愿军在极端严酷惨烈的环境下,凭借钢铁意志最终取得了长津湖战役的胜利,该电影也再次扻起了全民爱国热潮,国安民才安,有国才有家!据猫眼数据,截止10月8日,《长津湖》累计票房超过60亿,成为2021年全球票房冠军!该电影9月30日在莱芜的票房为6.7万元,接下来国庆假期7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房).
日期 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
票房(万元) +7.6 +2.7 +2.5 +4.7 +2 -0.6 -13.8
(1)国庆假期7天中,10月4日的票房收入是______万元;
(2)国庆假期7天中,票房收入最多的一天是10月______日;
(3)国庆假期7天中,求票房收入最多的一天比最少的一天多多少万元?
(1)解: 10月4日的票房收入是:6.7+7.6+2.7+2.5+4.7=24.2(万元),
故答案为:24.2;
(2)解:10月1日票房收入为:6.7+7.6=14.3(万元),
10月2日票房收入为:14.3+2.7=17(万元),
10月3日票房收入为:17+2.5=19.5(万元),
10月4日票房收入为:19.5+4.7=24.2(万元),
10月5日票房收入为:24.2+2=26.2(万元),
10月6日票房收入为:26.2 0.6=25.6(万元),
10月7日票房收入为:25.6 13.8=11.8(万元),
故国庆假期7天中,票房收入最多的一天是10月5日.
故答案为:5;
(3)解:26.2 11.8=14.4(万元),
故票房收入最多的一天比最少的一天多14.4万元.
例18.用科学记数法表示下列各数:
1000000,57000000,-123000000000
解:1000000=106,57000000=5.7×107,-123000000000=-1.23×1011
科学记数法及其应用
7
例19.下列用科学记数法写出的数,原数分别是什么数?
1×107,4×103, 8.5×106, 7.04×105, -3.96×104.
解:1×107=10000000, 4×103=4000, 8.5×106=8500000,
7.04×105=704000,-3.96×104=-39600.
【7-1】据统计,中国每年生产75亿支铅笔,需要大量木材.75亿用科学记数法表示为____________.
【7-2】天文学里常用“光年”作为距离单位.规定1“光年”为光一-年(365天)内传播的距离,光的传播速度为3×108米/秒,则用科学记数法表示1光年=_____________千米.
7.5×109
9.4608×1012
【7-3】生物学指出:生态系统中,每输入一个营养级的能量,大约只有10%的能量能够流动到下一个营养级,在H1→H2→H3→H4→H5→H6, 这条生物链中(Hn表示第n个营养级,n=1,2,…,6),要使H6获得30千焦的能量,则需要H1的提供的能量为多少千焦 (用科学记数法表示)
解:根据题意,得30×10×10×10×10×10
=3000000=3×106(千焦)
答:需要H1的提供的能量为3×106千焦.
近似数及其应用
8
(1)0.0158(精确到0.001);
(2)304.35(精确到个位);
(3)1.804(精确到0.1);
(4)1.804(精确到0.01).
例20.按括号内的要求,用四舍五入法对下列各数取近似数:
解:(1)0.0158 ≈0.016;(2)304.35≈304;
(3)1.804 ≈1.8; (4)1.804≈1.80.
对8四舍五入
对3四舍五入
对0四舍五入
对4四舍五入
近似数及其应用
8
例21.下列由四舍五入得到的近似数,各精确到哪一位?
(1)3200;(2)230万;(3)0.080;(4)6.2×103;(5)4.00万.
解:(1)近似数3200精确到个位;
(2)近似数230万精确到万位;
(3)近似数0.080精确到千分位;
(4)近似数6.2×103精确到百位;
(5)近似数4.00万精确到百位.
先把数还原,再看2所在的数位.
近似数及其应用
8
例22.数四舍五入后的近似值为1.30,则的取值范围是( )
A. B.
C. D.
【分析】根据四舍五入法的原则,保留两位小数的情况下,大于或等于1.295且小于1.305的数四舍五入后的近似值是1.30,
B
【8-1】下列各数是通过四舍五入得到的近似数:
(1) 0.600它精确到_______位; (2) 4.10×106精确到________位:
(3) 13.6万精确到________位.
【8-2】用四舍五入法,按要求取近似值:
(1) 0.05098 (精确到0.01)≈______;(2) 549.49 (精确到个位)≈______;
(3) 0.9999 (精确到0.1)≈_______.
千分
万
千
0.05
549
1.0
【8-3】近似数3.2的准确值a的取值范围是( )
A.3.1C
与有理数运算有关的规律问题
9
例23.(1)计算:①2-1=___;②22-2-1=___; ③23-22-2-1=___; ④24-23-22-2-1 =___; ⑤25-24-23-22-2-1=___.
(2)根据上面的计算结果猜想:
22020-22019-22018-…-22-2-1的值为____;
2n-2n-l-2n-2-.….-22-2-1的值为____.
(3)根据上面猜想的结论,求213-212-211-210-29-28-27-26的值.
1
1
1
1
1
1
1
解:由猜想的结论得:213-212-211-210-29-28-27-26-25-24-23-22-2-1=1
所以,213-212-211-210-29-28-27-26
=1+1+2+22+23+24+25
=1+2+4+8+16+32
=64
(3)根据上面猜想的结论,求213-212-211-210-29-28-27-26的值.
与有理数运算有关的规律问题
9
例24.如图,在数轴上,点表示1,现将点沿数轴做如下移动:第一次将点向左移动3个单位长度到达点,第2次将点向右平移6个单位长度到达点,第3次将点向左移动9个单位长度到达点…,则第2020次移动到点时,在数轴上对应的实数是_________.
与有理数运算有关的规律问题
9
3031
【9-1】求所有分母不超过100的正的真分数的和,即:=_______.
2475
【9-2】观察下列各式:1-=,1-=,1-=,根据上面的等式所反映的规律(1-)(1-)(1-)=________.
【9-3】观察下列等式:
……
请按上述规律,写出第个式子的计算结果(为正整数)______.(写出最简计算结果即可)
有理数章节复习
1.对本章知识要点进行复习梳理;
2.会运用有理数的运算法则、运算律,熟练进行有理数的运算; (重点、难点)
3.用科学记数法表示绝对值较大的数;
4.用四舍五入法,按要求(精确度)确定运算结果.
4.用正、负数表示具有相反意义的量.
一、正数和负数
1.像1,2,3,1.8%这样大于0的数叫做正数.
2.像-3,-1,-2,-2.7%这样在正数前面加上符号“-”(负)的数叫做负数.
3.0既不是正数,也不是负数.
5.具有相反意义的量应满足的条件:
①必须是同类量,而且是成对出现的;②只要求意义相反,不要求数量一定相等.
二、有理数的分类
注意: ①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
三、数轴
3.数轴的三要素
1.规定了原点、正方向、单位长度的直线叫做数轴.
2.任何一个有理数都可以用数轴上的一个点来表示.
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.(单位长度要一致)
0
0
1
2
3
-1
-2
-3
三、数轴
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻度均匀.
画数轴注意事项:
三、数轴
位置特征:1.分居原点左右;2.到原点距离相等.
a的相反数是-a ; 0的相反数是0
2
5
2
5
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
四、相反数
五、绝对值
1.定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,用“|a|”表示.
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
|a|≥0
2.绝对值的性质及应用
六、有理数大小的比较
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
七、有理数的运算
有理数加法运算的基本解题思路:
1.先判断类型(同号、异号等);2.再确定和的符号;3.最后进行绝对值的加减运算.
七、有理数的运算
(a+b)+c=a+(b+c)
a+b=b+a
1.加法交换律:在有理数加法中,两个数相加,交换加数的位置,和不变.
2.加法结合律:在有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
用字母表示为:
用字母表示为:
七、有理数的运算
有理数的减法法则是一个转化法则,减号转化为加号,同时要注意减数变为它的相反数,这样就可以用加法来解决减法问题.
七、有理数的运算
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
5.乘积是1的两个数互为倒数.
七、有理数的运算
法则二:两数相除,同号得正,异号得负,并把绝对值相除.
0除以任何一个不等于0的数,都得0.
法则一:除以一个不等于0的数,等于乘这个数的倒数.
1.有理数除法法则:
2.有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
3.乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
七、有理数的运算
3.乘方的符号法则:
(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数,负数的偶次幂是正数;(3)零的正整数次幂都是零.
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
2.组成要素
1.乘方的定义
七、有理数的运算
(1)看清运算,定运算顺序;
(2)根据特点,巧用运算律;
(3)选对法则,耐心计算.
2.有理数的加减乘除混合运算三步走:
【运算顺序】1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
1.有理数的混合运算
我们可以把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10), n是正整数.这种记数方法叫做科学记数法.
1.用科学计数法表示较大的数应注意以下两点:
1≤<10
当大数是大于10的整数时,n为整数位减去1.
2.灵活运用科学计数法,注意解题技巧,总结解题规律.
八、科学记数法
九、近似数
1.近似数:
(1)我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
(2)有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,2022年全国高考报名人数1193万人.
近似数与准确数的接近程度,可以用精确度表示.
2.精确度:
正数和负数的概念及其应用
1
例1.牛奶盒的包装上印有260±5ml,下列四盒送去质检,不合格的是( )
A.265ml B.262ml C.258ml D.250ml
【分析】解:∵牛奶盒的包装上印有260±5ml,
∴最大值为:260+5=265(ml),最小值为:260-5=255(ml),
∴选项A、B、C均合格,选项D不合格.
故选:D.
D
正数和负数的概念及其应用
1
例2.下列是具有相反意义的量是( )
A.身高增加1cm和体重减少1kg B.顺时针旋转90°和逆时针旋转45°
C.向右走2米和向西走5米 D.购买5本图书和借出4本图书
【分析】解:A、身高和体重不是相反的量,不符合题意;
B、顺时针旋转与逆时针旋转是具有相反意义的量,符合题意;
C、向右和向西不是相反的量,不符合题意;
D、购买和借出不是相反的量,不符合题意;
故选:B.
B
正数和负数的概念及其应用
1
例3.北京与柏林的时差为7小时,例如,北京时间14:00,同一时刻的柏林时间是7:00.小丽和小红分别在北京和柏林,她们相约在各自当地时间8:00~17:00之间选择一个时刻开始通话,这个时刻可以是北京时间( )
A.9:30 B.11:30 C.13:30 D.15:30
【分析】解:由题意得,柏林时间比北京时间早7小时,
当柏林时间为8:00,则北京时间为15:00;当北京时间为17:00,则柏林时间为10:00;
所以这个时间可以是北京时间的15:00到17:00之间,
故选:D.
D
【1-1】某运动项目的比赛规定,胜一场记作“+1”分,平局记作“0”分,如果某队得到“-1”分,则该队在比赛中( )
A.与对手打成平局 B.输给对手 C.打赢了对手 D.无法确定
【1-2】下列各组数中,具有相反意义的量是( )
A.盈利40元和运出货物20吨 B.向东走4千米和向南走4千米
C.身高180 cm和身高90cm D.收入500元和支出200元
B
D
城市 悉尼 纽约
时差/时 +2 -13
【1-3】纽约、悉尼与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京晚的时数):
当北京10月1日23时,悉尼、纽约的时间分别是 ( )
A.9月30日21时;9月30日10时 B.10月1日10时;10月2日10时
C.10月2日1时; 10月1日10时 D.9月30日21时;10月2日12时
C
有理数的相关概念、分类及其应用
2
例4. 下列各数中,是负整数的是( )
A.-23 B.-|-0.1| C.-(-) D.(-2)2
A
【分析】解:A.-23=-8,是负整数;
B.-|-0.1|=-0.1,是负分数不是负整数;
C.-(-)=,是正分数不是负整数;
D.(-2)2=4,是正整数不是负整数;
故选A.
例5.把下列各数填在相应的集合中:
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ }.
有理数的相关概念、分类及其应用
2
【2-1】下列说法正确的是( )
A.正有理数和负有理数组成全体有理数 B.零既不是正数,也不是负数
C.0.5既不是整数,也不是分数,因而它不是有理数 D.在有理数中,零的意义表示没有
【2-2】在 ,,,,,,, 中,
整数是________;正分数是_____________________;有理数有____个.
B
7
-17,0
,,,
【2-3】指出下列各数中的正数、负数、整数、分数:
-15,+6,-2,-0.9,1,,0,3,0.63,-4.95.
解:正数集合:{ }
负数集合:{ }
整数集合:{ }
分数集合:{ }
-15,-2,-0.9,-4.95,…
-15,+6,-2,1,0,…
-0.9,,3,0.63,-4.95,…
+6,1,3,0.63…
数轴、相反数、绝对值的概念及相关运算
3
例6.如果小虫在数轴上爬行了5个单位长度后停在表示﹣3的点上,那么小虫开始爬行的位置是表示( )的点.
A.﹣8 B.﹣2 C.﹣8或2 D.8或﹣2
C
分析:逆向思维.距离-3的点5个单位长度的点有两个,分别在-3的左边是-8;右边是2.
例7.若 ,则a=____,b=_____.
【解析】一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
解:因为
所以
所以
所以a=-5,b=3.
【点睛】几个非负数的和为0,则这几个数都为0.
3
-5
数轴、相反数、绝对值的概念及相关运算
3
数轴、相反数、绝对值的概念及相关运算
3
例8.点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:(1)b﹣a<0;(2)|a|<|b|;(3)a+b>0;(4)>0.其中正确的是( ) A.(1)(2) B.(2)(3) C.(3)(4) D.(1)(4)
【分析】解:根据图示,可得﹣3<a<0,b>3,
∴(1)b﹣a>0,故错误;(2)|a|<|b|,故正确;(3)a+b>0,故正确;(4)<0,故错误.故选B.
B
数轴、相反数、绝对值的概念及相关运算
3
例9.如果、、是非零有理数,且,那么的所有可能的值为_____.
【分析】、、为非零有理数,且
、、只能为两正一负或一正两负.
①当、、为两正一负时,设、为正,为负
原式
②当、、为一正两负时,设为正,、为负
原式综上,的值为.
0
例10.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索:
(1)计算|5-(-2)|=______;
(2)使得|x-1|+|x+5|=6这样的整数有_______________________(写出所有符合条件的整数);
(3)由以上探索猜想对于任何有理数x,式子|x-2|+|x+3.5|是否有最小值?________
数轴、相反数、绝对值的概念及相关运算
3
数轴、相反数、绝对值的概念及相关运算
3
解:(1),
故答案为:7;
(2)可以理解为:数轴上某点到1所对应的点的距离和到所对应的点的距离之和为6,满足条件的整数有:,,,,,0,1,
故答案为:,,,,,0,1;
(3)有,理解为:数轴上某点到2所对应的点的距离和到所对应的点的距离之和,其最小值为.
【3-1】点A为数轴上表示-1的动点,当点A沿数轴移动3个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-4 C.2或-4 D.不同于以上
C
【3-2】下列各对数中,互为相反数的有( )
①-1与+1;②+(+1)与-1;③-(-2)与+(-2);④-(-)与+(+) ;
⑤+[-(+1)]与-[+(-1)];⑥-(+2)与-(-2).
A.6对 B.5对 C.4对 D.3对
B
【3-3】在数轴上,a,b所表示的数如图所示,下列结论正确的是( )
A.a+b>0 B.|b|<|a| C.a﹣b>0 D.a b>0
C
【3-4】若,则______.
4
【3-5】|x﹣5|+|2﹣x|的最小值为_____.
3
有理数的大小比较
4
例11.比较下列各对数的大小.
(1) -(-1)和-(+2);(2)-和-;(3) -(-0.3)和|-|.
解:(1)先化简,-(-1)=1,-(+2)=-2
因为正数大于负数,
所以1>-2,即 -(-1)>-(+2)
(2)这是两个负数比较大小,先求它们的绝对值.
|-|= ,|-|= =
因为< ,即|-|<|-|,
所以->-
(3)先化简,-(-0.3)=0.3,|-|=
0.3< ,即-(-0.3)<|-|.
有理数的大小比较
4
例12.若、为有理数,,,且,那么,,,的大小关系是( )
A. B.
C. D.
C
【分析】解:∵,,且,
∴,,,
∴,
∴.故选:C.
【4-2】下列判断,正确的是( )
A.若a>b,则│a│>│b│ B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│ D.若a>b>0,则│a│>│b│
D
【4-3】绝对值大于1而不大于4的整数有__________________________.
-4、-3、-2、2、3、4
【4-1】下列四组有理数大小的比较正确的是( )
A.-> B.->- C.->- D.>
D
例13.计算:
(1)2×(-3)3-4×(-3)+15 (2)(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2)
解:(1)原式=2×(-27)-(-12)+15
=-54+12+15
=-27
(2)原式=-8+(-3)×(16+2)-9÷(-2)
=-8+(-3)×18-(-4.5)
=-8-54+4.5
=-57.5
有理数的运算
5
有理数的运算
5
例14.已知a,b互为相反数,c、d互为倒数,x的平方是4.试求x2-(a+b+cd)x
+(a+b)2000+(-cd)2020的值.
解:根据题意得,
a+b=0,cd=1,x2=4(即x=±2)
(1)当x=2时,原式=4-(0+1)×2+02000+(-1)2020=4-2+O+1=3
(2)当x=-2时,原式=4-(0+1)×(-2)+02000+(-1)2020=4-(-2)+O+1=7.
有理数的运算
5
例15.计算:
解:设,,,
而A+B==1,∴原式=.
【5-2】如图是一个计算程序,若输入a的值为-1,则输出的结果应为( )
A.7 B.﹣5 C.1 D.5
【5-1】计算﹣23+[(﹣4)2﹣(1﹣32)×3]= .
B
32
【5-3】现规定一种新的运算“☉”: a☉b=ab,如3☉2=32=9.则3等于( )
A. B.8 C. D.
A
例16.某公司去年1~3月平均每月亏损1.5万元,4~6月平均盈利2万元,7~10月平均盈利1.7万元,11~12月平均亏损2.3万元,这个公司去年总盈亏情况如何?
解:记盈利额为正数,亏损额为负数,公司去年全年总的盈亏(单位:万元)为
(-1.5)×3+2×3+1.7×4+(-2.3)×2
=-4.5+6+6.8-4.6
=3.7
答:这个公司去年全年盈利3.7万元.
有理数运算的实际应用
6
有理数运算的实际应用
6
例17.入冬以来,某品牌的羽绒服统计了在西乡市场某一周的销售情况,以每天100件为标准,超过的件数记作正数,不足的件数记作负数,记录如下:8,12,-9,6,-11,10,-2.
(1)求销量最多的一天比销量最少的一天多销售______件;
(2)该品牌羽绒服这一周的销售总量是多少件?若每件羽绒服的利润为130元,则这一周销售该品牌羽绒服的总利润为多少元?
有理数运算的实际应用
6
解:(1)(件)
(2)7×100+8+12+(-9)+6+(-11)+10+(-2)=714(件)
所以该品牌羽绒服这一周的销售总量是714件.
714×130=92820(元)
所以这一周销售该品牌羽绒服的总利润为92820元.
【6-1】某人用400元购买了8套儿童服装,准备以一定价格出售.他以每套55元的价格为标准,将超出的记作正数,不足的记作负数,记录如下:+2,-3,+2,+1,-2,-1,0,-2(单位:元).他卖完这8套儿童服装后是盈利还是亏损?他盈利(或亏损)了多少钱?
解:(元),
(元),
答:他盈利了37元.
【6-2】武汉百步亭小区交警每天都骑摩托车沿南北街来回巡逻,早晨从A地出发,晚上最后到达B地.假定向北为正方向,当天巡逻记录如下(单位:km):14,﹣9,18,﹣7,13,﹣6,10,﹣6,问:
(1)B地在A地什么位置?
(2)若摩托车每千米耗油0.1升,则一共需耗油多少升?
解:(1)14-9+18-7+13-6+10-6=14+18+13+10-9-7-6-6=27(km),
答:B在A正北27km;
(2)|14|+|﹣9|+|18|+|﹣7|+|13|+|﹣6|+|10|+|﹣6|=83(km),
83×0.1=8.3 (升 ),
答:一共需耗油8.3升.
【6-3】2021年国庆档电影《长津湖》以抗美援朝为背景,讲述了中国人民志愿军在极端严酷惨烈的环境下,凭借钢铁意志最终取得了长津湖战役的胜利,该电影也再次扻起了全民爱国热潮,国安民才安,有国才有家!据猫眼数据,截止10月8日,《长津湖》累计票房超过60亿,成为2021年全球票房冠军!该电影9月30日在莱芜的票房为6.7万元,接下来国庆假期7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房).
日期 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
票房(万元) +7.6 +2.7 +2.5 +4.7 +2 -0.6 -13.8
(1)国庆假期7天中,10月4日的票房收入是______万元;
(2)国庆假期7天中,票房收入最多的一天是10月______日;
(3)国庆假期7天中,求票房收入最多的一天比最少的一天多多少万元?
(1)解: 10月4日的票房收入是:6.7+7.6+2.7+2.5+4.7=24.2(万元),
故答案为:24.2;
(2)解:10月1日票房收入为:6.7+7.6=14.3(万元),
10月2日票房收入为:14.3+2.7=17(万元),
10月3日票房收入为:17+2.5=19.5(万元),
10月4日票房收入为:19.5+4.7=24.2(万元),
10月5日票房收入为:24.2+2=26.2(万元),
10月6日票房收入为:26.2 0.6=25.6(万元),
10月7日票房收入为:25.6 13.8=11.8(万元),
故国庆假期7天中,票房收入最多的一天是10月5日.
故答案为:5;
(3)解:26.2 11.8=14.4(万元),
故票房收入最多的一天比最少的一天多14.4万元.
例18.用科学记数法表示下列各数:
1000000,57000000,-123000000000
解:1000000=106,57000000=5.7×107,-123000000000=-1.23×1011
科学记数法及其应用
7
例19.下列用科学记数法写出的数,原数分别是什么数?
1×107,4×103, 8.5×106, 7.04×105, -3.96×104.
解:1×107=10000000, 4×103=4000, 8.5×106=8500000,
7.04×105=704000,-3.96×104=-39600.
【7-1】据统计,中国每年生产75亿支铅笔,需要大量木材.75亿用科学记数法表示为____________.
【7-2】天文学里常用“光年”作为距离单位.规定1“光年”为光一-年(365天)内传播的距离,光的传播速度为3×108米/秒,则用科学记数法表示1光年=_____________千米.
7.5×109
9.4608×1012
【7-3】生物学指出:生态系统中,每输入一个营养级的能量,大约只有10%的能量能够流动到下一个营养级,在H1→H2→H3→H4→H5→H6, 这条生物链中(Hn表示第n个营养级,n=1,2,…,6),要使H6获得30千焦的能量,则需要H1的提供的能量为多少千焦 (用科学记数法表示)
解:根据题意,得30×10×10×10×10×10
=3000000=3×106(千焦)
答:需要H1的提供的能量为3×106千焦.
近似数及其应用
8
(1)0.0158(精确到0.001);
(2)304.35(精确到个位);
(3)1.804(精确到0.1);
(4)1.804(精确到0.01).
例20.按括号内的要求,用四舍五入法对下列各数取近似数:
解:(1)0.0158 ≈0.016;(2)304.35≈304;
(3)1.804 ≈1.8; (4)1.804≈1.80.
对8四舍五入
对3四舍五入
对0四舍五入
对4四舍五入
近似数及其应用
8
例21.下列由四舍五入得到的近似数,各精确到哪一位?
(1)3200;(2)230万;(3)0.080;(4)6.2×103;(5)4.00万.
解:(1)近似数3200精确到个位;
(2)近似数230万精确到万位;
(3)近似数0.080精确到千分位;
(4)近似数6.2×103精确到百位;
(5)近似数4.00万精确到百位.
先把数还原,再看2所在的数位.
近似数及其应用
8
例22.数四舍五入后的近似值为1.30,则的取值范围是( )
A. B.
C. D.
【分析】根据四舍五入法的原则,保留两位小数的情况下,大于或等于1.295且小于1.305的数四舍五入后的近似值是1.30,
B
【8-1】下列各数是通过四舍五入得到的近似数:
(1) 0.600它精确到_______位; (2) 4.10×106精确到________位:
(3) 13.6万精确到________位.
【8-2】用四舍五入法,按要求取近似值:
(1) 0.05098 (精确到0.01)≈______;(2) 549.49 (精确到个位)≈______;
(3) 0.9999 (精确到0.1)≈_______.
千分
万
千
0.05
549
1.0
【8-3】近似数3.2的准确值a的取值范围是( )
A.3.1
与有理数运算有关的规律问题
9
例23.(1)计算:①2-1=___;②22-2-1=___; ③23-22-2-1=___; ④24-23-22-2-1 =___; ⑤25-24-23-22-2-1=___.
(2)根据上面的计算结果猜想:
22020-22019-22018-…-22-2-1的值为____;
2n-2n-l-2n-2-.….-22-2-1的值为____.
(3)根据上面猜想的结论,求213-212-211-210-29-28-27-26的值.
1
1
1
1
1
1
1
解:由猜想的结论得:213-212-211-210-29-28-27-26-25-24-23-22-2-1=1
所以,213-212-211-210-29-28-27-26
=1+1+2+22+23+24+25
=1+2+4+8+16+32
=64
(3)根据上面猜想的结论,求213-212-211-210-29-28-27-26的值.
与有理数运算有关的规律问题
9
例24.如图,在数轴上,点表示1,现将点沿数轴做如下移动:第一次将点向左移动3个单位长度到达点,第2次将点向右平移6个单位长度到达点,第3次将点向左移动9个单位长度到达点…,则第2020次移动到点时,在数轴上对应的实数是_________.
与有理数运算有关的规律问题
9
3031
【9-1】求所有分母不超过100的正的真分数的和,即:=_______.
2475
【9-2】观察下列各式:1-=,1-=,1-=,根据上面的等式所反映的规律(1-)(1-)(1-)=________.
【9-3】观察下列等式:
……
请按上述规律,写出第个式子的计算结果(为正整数)______.(写出最简计算结果即可)
