12.2.4 直角三角形全等的判定(HL) 课件(共21张PPT)
文档属性
| 名称 | 12.2.4 直角三角形全等的判定(HL) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 10:57:55 | ||
图片预览


文档简介
(共21张PPT)
直角三角形全等的判定
---HL
1.探索并理解直角三角形全等的判定方法“HL”.(难点)
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.(重点)
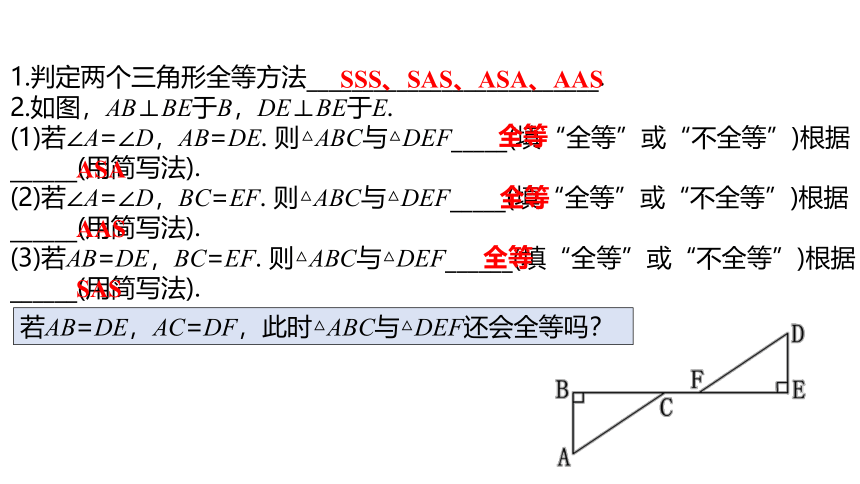
1.判定两个三角形全等方法__________________________.
2.如图,AB⊥BE于B,DE⊥BE于E.
(1)若∠A=∠D,AB=DE. 则△ABC与△DEF_____(填“全等”或“不全等”)根据______(用简写法).
(2)若∠A=∠D,BC=EF. 则△ABC与△DEF_____(填“全等”或“不全等”)根据______(用简写法).
(3)若AB=DE,BC=EF. 则△ABC与△DEF______(填“全等”或“不全等”)根据______(用简写法).
SSS、SAS、ASA、AAS
ASA
全等
全等
全等
AAS
SAS
若AB=DE,AC=DF,此时△ABC与△DEF还会全等吗?
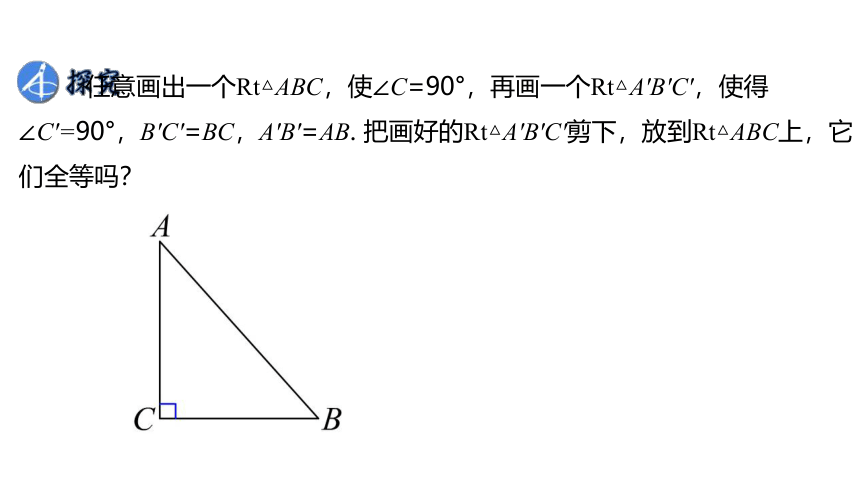
任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′,使得∠C′=90°,B′C′=BC,A′B′=AB. 把画好的Rt△A′B′C′剪下,放到Rt△ABC上,它们全等吗?
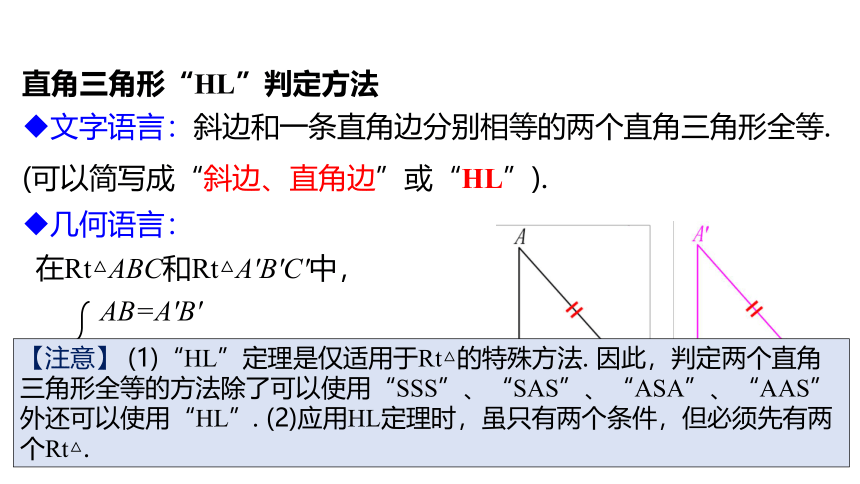
文字语言:斜边和一条直角边分别相等的两个直角三角形全等.
(可以简写成“斜边、直角边”或“HL”).
直角三角形“HL”判定方法
在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′
BC=B′C′
几何语言:
【注意】 (1)“HL”定理是仅适用于Rt△的特殊方法. 因此,判定两个直角三角形全等的方法除了可以使用“SSS”、“SAS”、“ASA”、“AAS”外还可以使用“HL”. (2)应用HL定理时,虽只有两个条件,但必须先有两个Rt△.
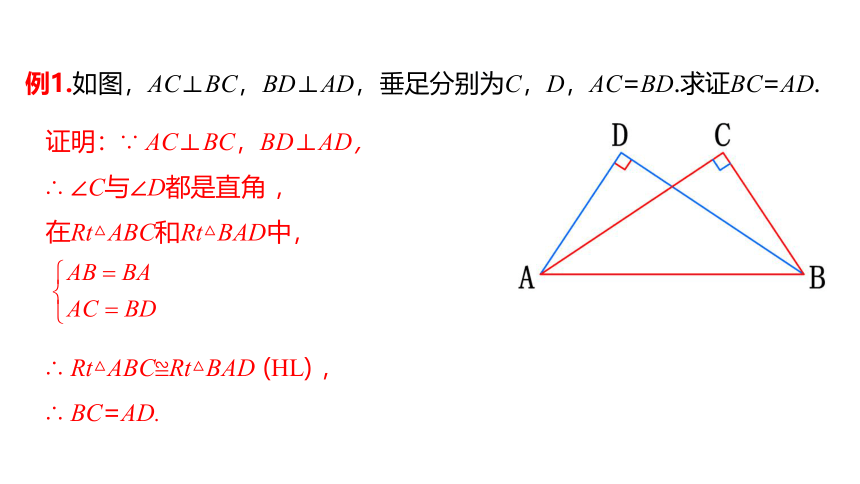
例1.如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证BC=AD.
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C与∠D都是直角 ,
在Rt△ABC和Rt△BAD中,
∴ Rt△ABC≌Rt△BAD (HL) ,
∴ BC=AD.
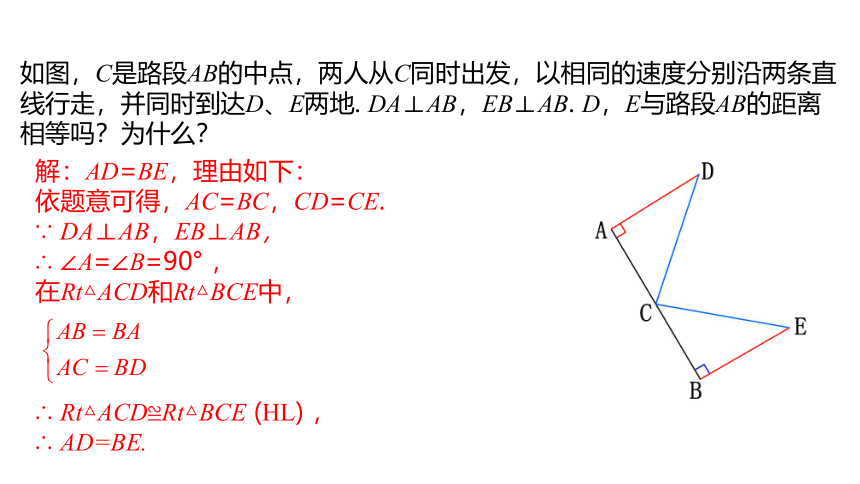
如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D、E两地. DA⊥AB,EB⊥AB. D,E与路段AB的距离相等吗?为什么?
解:AD=BE,理由如下:
依题意可得,AC=BC,CD=CE.
∵ DA⊥AB,EB⊥AB,
∴ ∠A=∠B=90° ,
在Rt△ACD和Rt△BCE中,
∴ Rt△ACD≌Rt△BCE (HL) ,
∴ AD=BE.
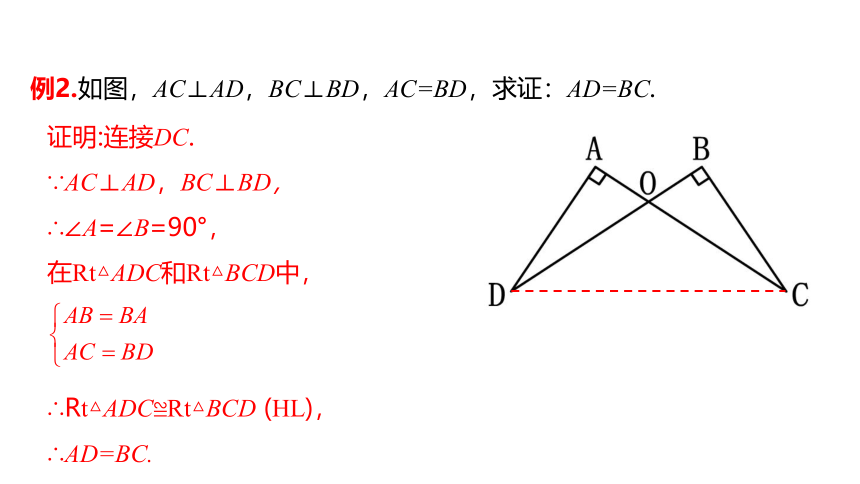
例2.如图,AC⊥AD,BC⊥BD,AC=BD,求证:AD=BC.
证明:连接DC.
∵AC⊥AD,BC⊥BD,
∴∠A=∠B=90°,
在Rt△ADC和Rt△BCD中,
∴Rt△ADC≌Rt△BCD (HL),
∴AD=BC.
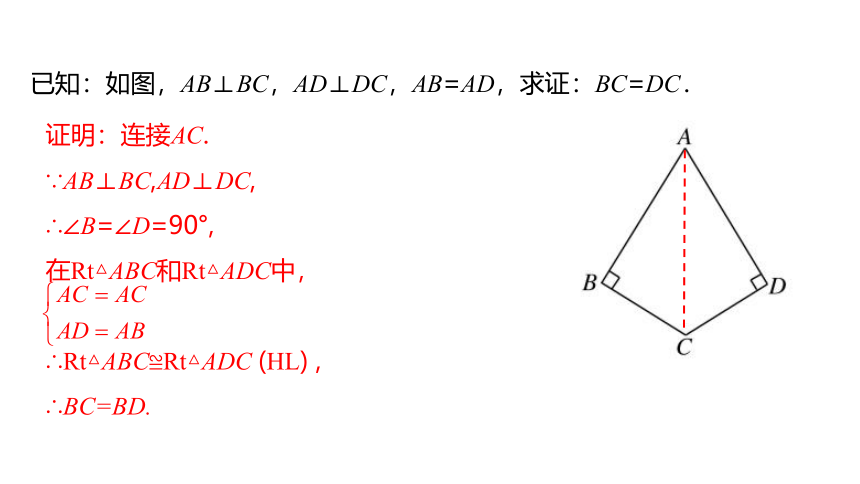
已知:如图,AB⊥BC,AD⊥DC,AB=AD,求证:BC=DC.
证明:连接AC.
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC (HL) ,
∴BC=BD.
例3.如图,已知AD是△ABC的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为E、F.求证BE=CF.
证明:AD平分∠BAC,∴∠BAD=∠CAD,
∵DE、DF分别垂直于AB、AC,
∴∠AED=∠AFD=90°,
在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴DE=DF,
在Rt△BDE和Rt△CDF中,
∴ Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
已知:如图,点A、E、C同一条直线上,AB⊥BC,AD⊥DC,AB=AD.
求证:BE=DE.
证明:∵AB⊥BC,AD⊥DC,
∴在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAE=∠DAE,
在Rt△ABE和Rt△ADE中,
∴Rt△ABE≌Rt△ADE(SAS),
∴BE=DE.
例4.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于E,点F在边AC上,连接DF.
(1)求证:AC=AE;
(2)若DF=DB,试说明∠B与∠AFD的数量关系;
(3)在(2)的条件下,若AB=m,AF=n,求BE的长(用含m,n的代数式表示).
(1)证明:∵∠C=90°,DE⊥AB,
∴∠C=∠AED=90°,
在△ACD和△AED中,
∴△ACD≌△AED(AAS),
∴AC=AE.
例4.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于E,点F在边AC上,连接DF.
(2)若DF=DB,试说明∠B与∠AFD的数量关系;
(2)解:∠B+∠AFD=180°,理由如下:
由(1)得:△ACD≌△AED,
∴DC=DE,
在Rt△CDF和Rt△EDB中,
∴Rt△CDF≌Rt△EDB(HL),
∴∠CFD=∠B,
∵∠CFD+∠AFD=180°,
∴∠B+∠AFD=180°.
例4.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于E,点F在边AC上,连接DF.
(3)在(2)的条件下,若AB=m,AF=n,求BE的长(用含m,n的代数式表示).
(3)解:由(2)知,Rt△CDF≌Rt△EDB,
∴CF=BE,
由(1)知AC=AE,
∵AB=AE+BE,
∴AB=AC+BE,
∵AC=AF+CF,
∴AB=AF+2BE,
∵AB=m,AF=n,
∴BE=(m﹣n).
1.判定两个直角三角形全等的方法有________________________________.
2.如图,已知∠C=∠D=90°,要使△ABC≌△BAD还需增加一个什么条件 把增加的条件填在横线上,并在后面相应括号内填上判定它们全等的理由.
(1)________________( )(2)________________( ) (3)________________( )(4)________________( )
3.如图,AB=AC,AD⊥BC,垂足为D,若BC=10cm,则BD=______cm.
SSS、SAS、ASA、AAS、HL
BC=AD
AC=BD
HL
∠CAB=∠DBA
HL
AAS
AAS
∠CBA=∠DAB
5
4.如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E、F,CE=BF.求证AE=DF.
证明:∵BF=CE,
∴BF-EF=CE-EF,
即BE=CF,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,
在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF(HL),
∴AE=DF.
5.如图,已知,AB⊥BD于B,ED⊥BD于D,AB=CD,AC=CE.
求证:AC⊥CE.
证明:AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,
在Rt△ABC和Rt△CDE中,
∴Rt△ABC≌Rt△CDE(HL),
∴∠A=∠ECD,
∵∠A+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°,
即AC⊥CE.
6.如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
【分析】总共可组成的命题(不论真假)有:
①②③ ④;①②④ ③;
①③④ ②;②③④ ①.
共4个命题,其中真命题有2个:
①②④ ③和①③④ ②
6.如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS),
∴∠ABC=∠DEF.
①②④
③
6.如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴AC=DF.
①③④
②
文字语言:斜边和一条直角边分别相等的两个直角三角形全等.
(可以简写成“斜边、直角边”或“HL”).
直角三角形“HL”判定方法
在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′
BC=B′C′
几何语言:
直角三角形全等的判定
---HL
1.探索并理解直角三角形全等的判定方法“HL”.(难点)
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.(重点)
1.判定两个三角形全等方法__________________________.
2.如图,AB⊥BE于B,DE⊥BE于E.
(1)若∠A=∠D,AB=DE. 则△ABC与△DEF_____(填“全等”或“不全等”)根据______(用简写法).
(2)若∠A=∠D,BC=EF. 则△ABC与△DEF_____(填“全等”或“不全等”)根据______(用简写法).
(3)若AB=DE,BC=EF. 则△ABC与△DEF______(填“全等”或“不全等”)根据______(用简写法).
SSS、SAS、ASA、AAS
ASA
全等
全等
全等
AAS
SAS
若AB=DE,AC=DF,此时△ABC与△DEF还会全等吗?
任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′,使得∠C′=90°,B′C′=BC,A′B′=AB. 把画好的Rt△A′B′C′剪下,放到Rt△ABC上,它们全等吗?
文字语言:斜边和一条直角边分别相等的两个直角三角形全等.
(可以简写成“斜边、直角边”或“HL”).
直角三角形“HL”判定方法
在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′
BC=B′C′
几何语言:
【注意】 (1)“HL”定理是仅适用于Rt△的特殊方法. 因此,判定两个直角三角形全等的方法除了可以使用“SSS”、“SAS”、“ASA”、“AAS”外还可以使用“HL”. (2)应用HL定理时,虽只有两个条件,但必须先有两个Rt△.
例1.如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证BC=AD.
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C与∠D都是直角 ,
在Rt△ABC和Rt△BAD中,
∴ Rt△ABC≌Rt△BAD (HL) ,
∴ BC=AD.
如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D、E两地. DA⊥AB,EB⊥AB. D,E与路段AB的距离相等吗?为什么?
解:AD=BE,理由如下:
依题意可得,AC=BC,CD=CE.
∵ DA⊥AB,EB⊥AB,
∴ ∠A=∠B=90° ,
在Rt△ACD和Rt△BCE中,
∴ Rt△ACD≌Rt△BCE (HL) ,
∴ AD=BE.
例2.如图,AC⊥AD,BC⊥BD,AC=BD,求证:AD=BC.
证明:连接DC.
∵AC⊥AD,BC⊥BD,
∴∠A=∠B=90°,
在Rt△ADC和Rt△BCD中,
∴Rt△ADC≌Rt△BCD (HL),
∴AD=BC.
已知:如图,AB⊥BC,AD⊥DC,AB=AD,求证:BC=DC.
证明:连接AC.
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC (HL) ,
∴BC=BD.
例3.如图,已知AD是△ABC的角平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为E、F.求证BE=CF.
证明:AD平分∠BAC,∴∠BAD=∠CAD,
∵DE、DF分别垂直于AB、AC,
∴∠AED=∠AFD=90°,
在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴DE=DF,
在Rt△BDE和Rt△CDF中,
∴ Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
已知:如图,点A、E、C同一条直线上,AB⊥BC,AD⊥DC,AB=AD.
求证:BE=DE.
证明:∵AB⊥BC,AD⊥DC,
∴在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAE=∠DAE,
在Rt△ABE和Rt△ADE中,
∴Rt△ABE≌Rt△ADE(SAS),
∴BE=DE.
例4.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于E,点F在边AC上,连接DF.
(1)求证:AC=AE;
(2)若DF=DB,试说明∠B与∠AFD的数量关系;
(3)在(2)的条件下,若AB=m,AF=n,求BE的长(用含m,n的代数式表示).
(1)证明:∵∠C=90°,DE⊥AB,
∴∠C=∠AED=90°,
在△ACD和△AED中,
∴△ACD≌△AED(AAS),
∴AC=AE.
例4.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于E,点F在边AC上,连接DF.
(2)若DF=DB,试说明∠B与∠AFD的数量关系;
(2)解:∠B+∠AFD=180°,理由如下:
由(1)得:△ACD≌△AED,
∴DC=DE,
在Rt△CDF和Rt△EDB中,
∴Rt△CDF≌Rt△EDB(HL),
∴∠CFD=∠B,
∵∠CFD+∠AFD=180°,
∴∠B+∠AFD=180°.
例4.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于E,点F在边AC上,连接DF.
(3)在(2)的条件下,若AB=m,AF=n,求BE的长(用含m,n的代数式表示).
(3)解:由(2)知,Rt△CDF≌Rt△EDB,
∴CF=BE,
由(1)知AC=AE,
∵AB=AE+BE,
∴AB=AC+BE,
∵AC=AF+CF,
∴AB=AF+2BE,
∵AB=m,AF=n,
∴BE=(m﹣n).
1.判定两个直角三角形全等的方法有________________________________.
2.如图,已知∠C=∠D=90°,要使△ABC≌△BAD还需增加一个什么条件 把增加的条件填在横线上,并在后面相应括号内填上判定它们全等的理由.
(1)________________( )(2)________________( ) (3)________________( )(4)________________( )
3.如图,AB=AC,AD⊥BC,垂足为D,若BC=10cm,则BD=______cm.
SSS、SAS、ASA、AAS、HL
BC=AD
AC=BD
HL
∠CAB=∠DBA
HL
AAS
AAS
∠CBA=∠DAB
5
4.如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E、F,CE=BF.求证AE=DF.
证明:∵BF=CE,
∴BF-EF=CE-EF,
即BE=CF,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,
在Rt△ABE和Rt△DCF中,
∴Rt△ABE≌Rt△DCF(HL),
∴AE=DF.
5.如图,已知,AB⊥BD于B,ED⊥BD于D,AB=CD,AC=CE.
求证:AC⊥CE.
证明:AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,
在Rt△ABC和Rt△CDE中,
∴Rt△ABC≌Rt△CDE(HL),
∴∠A=∠ECD,
∵∠A+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°,
即AC⊥CE.
6.如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
【分析】总共可组成的命题(不论真假)有:
①②③ ④;①②④ ③;
①③④ ②;②③④ ①.
共4个命题,其中真命题有2个:
①②④ ③和①③④ ②
6.如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS),
∴∠ABC=∠DEF.
①②④
③
6.如图,在△ABC和△ADE中,B,E,C,F在同一直线上,下面有四个条件,请你在其中选3个作为题设,余下的1个作为结论,写一个真命题,并加以证明.①AB=DE,②AC=DF,③∠ABC=∠DEF,④BE=CF.
己知:____________(填序号),求证:____________(填序号)
证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴AC=DF.
①③④
②
文字语言:斜边和一条直角边分别相等的两个直角三角形全等.
(可以简写成“斜边、直角边”或“HL”).
直角三角形“HL”判定方法
在Rt△ABC和Rt△A′B′C′中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′
BC=B′C′
几何语言:
