12.1 全等三角形 课件(共25张PPT)
文档属性
| 名称 | 12.1 全等三角形 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 16:33:00 | ||
图片预览






文档简介
(共25张PPT)
全等三角形
1.理解并掌握全等三角形的概念及其基本性质.(重点)
2.能找准全等三角形的对应边,理解全等三角形的对应角相等.(难点)
3.能进行简单的推理和计算,并解决一些实际问题.(难点)
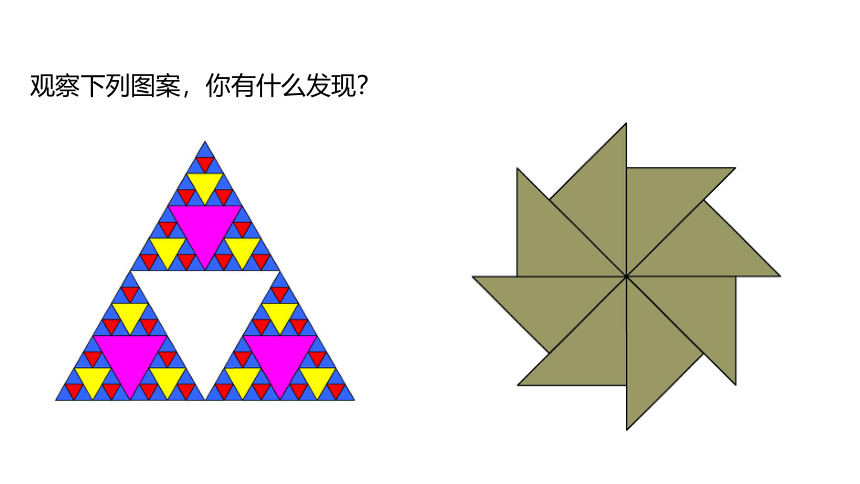
观察下列图案,你有什么发现?
观察下列图案,你有什么发现?
能够完全重合的两个图形叫做全等形.
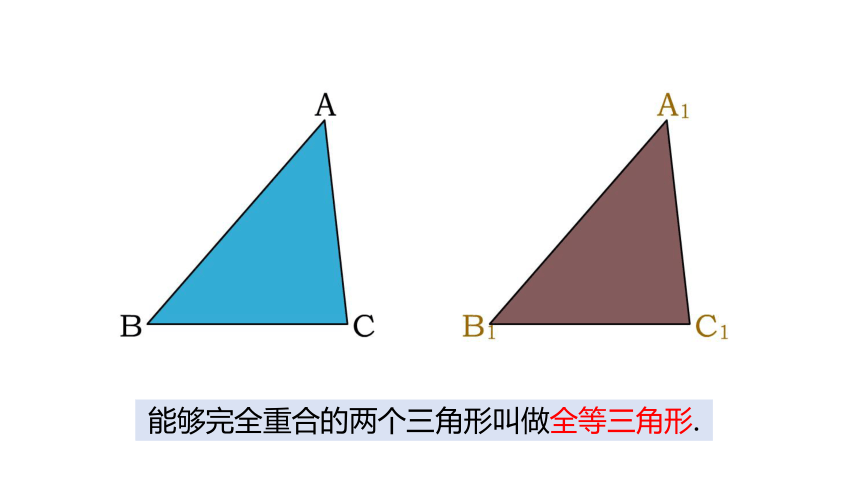
把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺形状、大小完全一样吗?把三角尺和裁得的纸板放在一起能够完全重合吗?
能够完全重合的两个三角形叫做全等三角形.
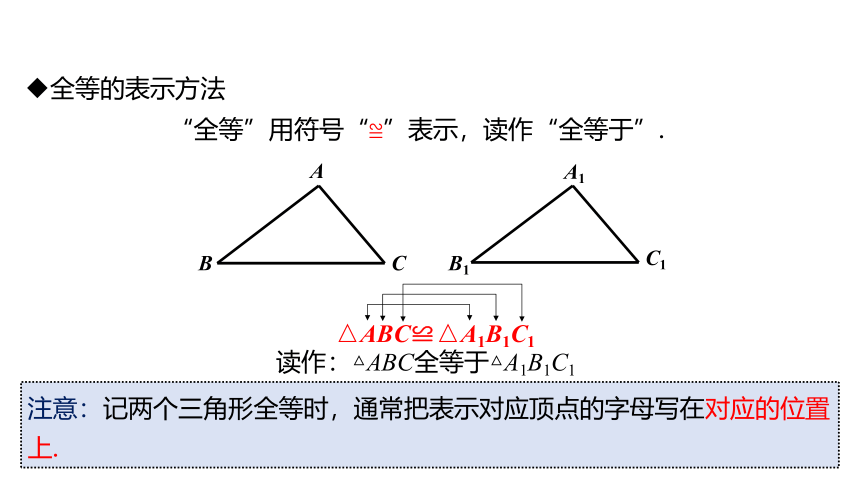
△ABC≌△A1B1C1
A
B
C
C1
B1
A1
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
读作:△ABC全等于△A1B1C1
重合的顶点叫对应顶点.
重合的边叫对应边.
重合的角叫对应角.
如点A和点A1,点B和点B1,点C和点C1
如AB和A1B1,AC和A1C1,BC和B1C1
如∠A和∠A1, ∠B和∠B1, ∠C和∠C1
△ABC≌△A1B1C1,对应边有什么关系?对应角呢?
AB=A1B1,AC=A1C1,BC=B1C1
∠A=∠A1, ∠B=∠B1, ∠C=∠C1
性质:全等三角形的对应边相等,全等三角形的对应角相等.
几何语言:
∵ △ABC≌△A1B1C1
∴ AB=A1B1,AC=A1C1,BC=B1C1,∠A=∠A1,∠B=∠B1,∠C=∠C1
在图(1)中,把△ABC沿直线BC平移,得到△DEF;
在图(2)中,把△ABC沿直线BC翻折180°,得到△DBC;
在图(3)中,把△ABC绕点A旋转,得到△ADE.
各图中的两个三角形全等吗?
△ABC≌△DEF △ABC≌△DBC △ABC≌△ADE
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.
请说出每图中的对应顶点,对应边、对应角.
例1.找一找下列全等图形的对应元素?
A
D
F
C
E
B
1
2
A
B
C
D
F
解:对应顶点:A与D,B与E,C与F;
对应边:AB=DE,AC=DF,BC=EF;
对应角:∠A=∠D,∠B=∠1,∠2=∠F.
解:对应顶点:A与A,B与F,C与D;
对应边:AB=AF,AC=AD,BC=FD;
对应角:∠B=∠F,∠ACB=∠ADF,∠BAC=∠FAD.
A
B
D
C
E
A
B
C
F
例1.找一找下列全等图形的对应元素?
解:对应顶点:A与A,B与E,C与F;
对应边:AB=AE,AC=AF,BC=EF;
对应角:∠BAC=∠EAF,∠B=∠E,∠C=∠F.
解:对应顶点:A与C,B与D,C与A;
对应边:AB=CD,AC=CA,BC=DA;
对应角:∠B=∠D,∠ACB=∠CAD,∠BAC=∠ACD.
寻找对应元素的规律
1. 有公共边的,公共边是对应边;
2. 有公共角的,公共角是对应角;
3. 有对顶角的,对顶角是对应角;
4. 两个全等三角形最大的边是对应边,最小的边也是对应边;
5. 两个全等三角形最大的角是对应角,最小的角也是对应角.
例2.如图,点A、B,C、D在同一条直线上,△ACE≌△DBF ,已知AC=5 ,BC=2,求AD的长.
解: ∵△ACE≌△DBF,
∴AC=BD.
∵AC=5,BC=2,
∴CD=BD-BC=AC-BC=3,
∴AD=AC+CD=5+3=8.
如图,△ABC≌△DEC,∠ACB=90°,且∠DCB=126°,求∠ACE的度数.
解:∵ △ABC≌△DEC ,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠DCE+∠ACB-∠DCB
=180°-126°
=54°.
例3.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
例3.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
(2)解:∵ BC∥DE ,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时, BC∥DE .
如图,△ABC沿BC方向平移到△DEF的位置.
(1)若∠B=30°,∠F=45°,求∠A的度数;
(2)若BF=10,EC=4,求平移的距离.
解:(1)由平移可知△ABC≌△DEF ,
∴∠ACB=∠F=45° ,
∴∠A=180°-∠B-∠ACB=105°.
(2)由平移可知△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF=(BF-EC)=3,
∴平移的距离BE为3.
1.△ABC沿BC折叠,使点A与点D重合,则△ABC_____△DBC,AB的对应边是_______,∠ACB的对应角是_________.
2.△ABC≌△CDA,则AB=_____,∠BAC=________.
3.△ABC≌△BAD,若AB=6cm,BD=5cm,AD=4cm,则BC=______cm;
4.△ABC≌△EFC,且CF=3cm,CE=5cm,∠EFC=57°,则∠A=____,BE=_____cm.
≌
DB
∠DCB
CD
∠DCA
4
33°
2
5.下列各选项中的两个图形属于全等图形的是( )
A. B. C. D.
B
6.下列说法正确的是( )
A.两个面积相等的图形一定是全等形
B.两个等边三角形是全等形
C.若两个图形的周长相等,则它们一定是全等形
D.两个全等图形的面积一定相等
D
7.如图,是一个的正方形网格,则∠1+∠2+∠3+∠4=________.
180°
8.沿网格线把正方形分割成两个全等图形?用两种不同的方法试一试.
全等
三角形
定义
能够完全重合的两个三角形叫做全等三角形
基本性质
对应边相等
对应角相等
对应元素确定方法
对应边
对应角
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
全等三角形
1.理解并掌握全等三角形的概念及其基本性质.(重点)
2.能找准全等三角形的对应边,理解全等三角形的对应角相等.(难点)
3.能进行简单的推理和计算,并解决一些实际问题.(难点)
观察下列图案,你有什么发现?
观察下列图案,你有什么发现?
能够完全重合的两个图形叫做全等形.
把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺形状、大小完全一样吗?把三角尺和裁得的纸板放在一起能够完全重合吗?
能够完全重合的两个三角形叫做全等三角形.
△ABC≌△A1B1C1
A
B
C
C1
B1
A1
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
读作:△ABC全等于△A1B1C1
重合的顶点叫对应顶点.
重合的边叫对应边.
重合的角叫对应角.
如点A和点A1,点B和点B1,点C和点C1
如AB和A1B1,AC和A1C1,BC和B1C1
如∠A和∠A1, ∠B和∠B1, ∠C和∠C1
△ABC≌△A1B1C1,对应边有什么关系?对应角呢?
AB=A1B1,AC=A1C1,BC=B1C1
∠A=∠A1, ∠B=∠B1, ∠C=∠C1
性质:全等三角形的对应边相等,全等三角形的对应角相等.
几何语言:
∵ △ABC≌△A1B1C1
∴ AB=A1B1,AC=A1C1,BC=B1C1,∠A=∠A1,∠B=∠B1,∠C=∠C1
在图(1)中,把△ABC沿直线BC平移,得到△DEF;
在图(2)中,把△ABC沿直线BC翻折180°,得到△DBC;
在图(3)中,把△ABC绕点A旋转,得到△ADE.
各图中的两个三角形全等吗?
△ABC≌△DEF △ABC≌△DBC △ABC≌△ADE
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.
请说出每图中的对应顶点,对应边、对应角.
例1.找一找下列全等图形的对应元素?
A
D
F
C
E
B
1
2
A
B
C
D
F
解:对应顶点:A与D,B与E,C与F;
对应边:AB=DE,AC=DF,BC=EF;
对应角:∠A=∠D,∠B=∠1,∠2=∠F.
解:对应顶点:A与A,B与F,C与D;
对应边:AB=AF,AC=AD,BC=FD;
对应角:∠B=∠F,∠ACB=∠ADF,∠BAC=∠FAD.
A
B
D
C
E
A
B
C
F
例1.找一找下列全等图形的对应元素?
解:对应顶点:A与A,B与E,C与F;
对应边:AB=AE,AC=AF,BC=EF;
对应角:∠BAC=∠EAF,∠B=∠E,∠C=∠F.
解:对应顶点:A与C,B与D,C与A;
对应边:AB=CD,AC=CA,BC=DA;
对应角:∠B=∠D,∠ACB=∠CAD,∠BAC=∠ACD.
寻找对应元素的规律
1. 有公共边的,公共边是对应边;
2. 有公共角的,公共角是对应角;
3. 有对顶角的,对顶角是对应角;
4. 两个全等三角形最大的边是对应边,最小的边也是对应边;
5. 两个全等三角形最大的角是对应角,最小的角也是对应角.
例2.如图,点A、B,C、D在同一条直线上,△ACE≌△DBF ,已知AC=5 ,BC=2,求AD的长.
解: ∵△ACE≌△DBF,
∴AC=BD.
∵AC=5,BC=2,
∴CD=BD-BC=AC-BC=3,
∴AD=AC+CD=5+3=8.
如图,△ABC≌△DEC,∠ACB=90°,且∠DCB=126°,求∠ACE的度数.
解:∵ △ABC≌△DEC ,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠DCE+∠ACB-∠DCB
=180°-126°
=54°.
例3.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
例3.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
(2)解:∵ BC∥DE ,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时, BC∥DE .
如图,△ABC沿BC方向平移到△DEF的位置.
(1)若∠B=30°,∠F=45°,求∠A的度数;
(2)若BF=10,EC=4,求平移的距离.
解:(1)由平移可知△ABC≌△DEF ,
∴∠ACB=∠F=45° ,
∴∠A=180°-∠B-∠ACB=105°.
(2)由平移可知△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF=(BF-EC)=3,
∴平移的距离BE为3.
1.△ABC沿BC折叠,使点A与点D重合,则△ABC_____△DBC,AB的对应边是_______,∠ACB的对应角是_________.
2.△ABC≌△CDA,则AB=_____,∠BAC=________.
3.△ABC≌△BAD,若AB=6cm,BD=5cm,AD=4cm,则BC=______cm;
4.△ABC≌△EFC,且CF=3cm,CE=5cm,∠EFC=57°,则∠A=____,BE=_____cm.
≌
DB
∠DCB
CD
∠DCA
4
33°
2
5.下列各选项中的两个图形属于全等图形的是( )
A. B. C. D.
B
6.下列说法正确的是( )
A.两个面积相等的图形一定是全等形
B.两个等边三角形是全等形
C.若两个图形的周长相等,则它们一定是全等形
D.两个全等图形的面积一定相等
D
7.如图,是一个的正方形网格,则∠1+∠2+∠3+∠4=________.
180°
8.沿网格线把正方形分割成两个全等图形?用两种不同的方法试一试.
全等
三角形
定义
能够完全重合的两个三角形叫做全等三角形
基本性质
对应边相等
对应角相等
对应元素确定方法
对应边
对应角
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
