22.1.3 二次函数y=a(x-h)^2+k的图象和性质 课件(共22张PPT)
文档属性
| 名称 | 22.1.3 二次函数y=a(x-h)^2+k的图象和性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 20:49:14 | ||
图片预览





文档简介
(共22张PPT)
人教版九年级(上)数学教学课件
第22章 二次函数
22.1 二次函数的图象和性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
22.1.3 二次函数y=a(x-h)2+k的图象和性质
情境导入
温故知新
二次函数的图像和性质
已知二次函数①y=-x2;②y= x2;③y=15x2;④y=-4x2;
⑤y= x2;⑥y=4x2.
(1)其中开口向上的有 (填题号);
(2)其中开口向下,且开口最大的是 (填题号);
(3)当自变量由小到大变化时,函数值先逐渐变大,然后逐渐变小的有 (填题号).
②③⑥
⑤
①④⑤
y=ax2+k的图象和性质
01
y=a(x-h)2的图象和性质
02
y=a(x-h)2+k的图象和性质
03
知识要点
精讲精练
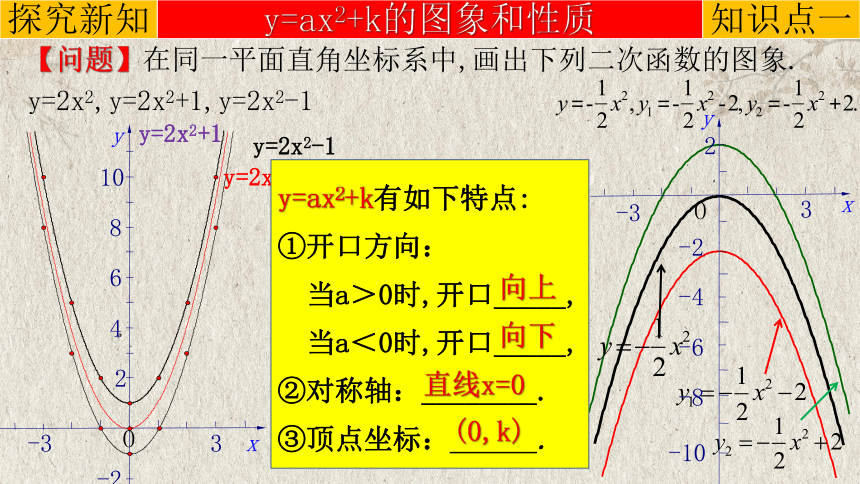
【问题】在同一平面直角坐标系中,画出下列二次函数的图象.
y=2x2+1
10
8
6
4
2
-2
-3
3
x
y
y=2x2-1
y=2x2
O
y=2x2,y=2x2+1,y=2x2-1
2
-2
-4
-6
-8
-10
-3
3
x
y
O
y=ax2+k有如下特点:
①开口方向:
当a>0时,开口_____,
当a<0时,开口_____,
②对称轴:________.
③顶点坐标:______.
向上
向下
直线x=0
(0,k)
知识点一
探究新知
y=ax2+k的图象和性质
解析式
y=2x2
y=2x2+1
y=2x2-1
+1
-1
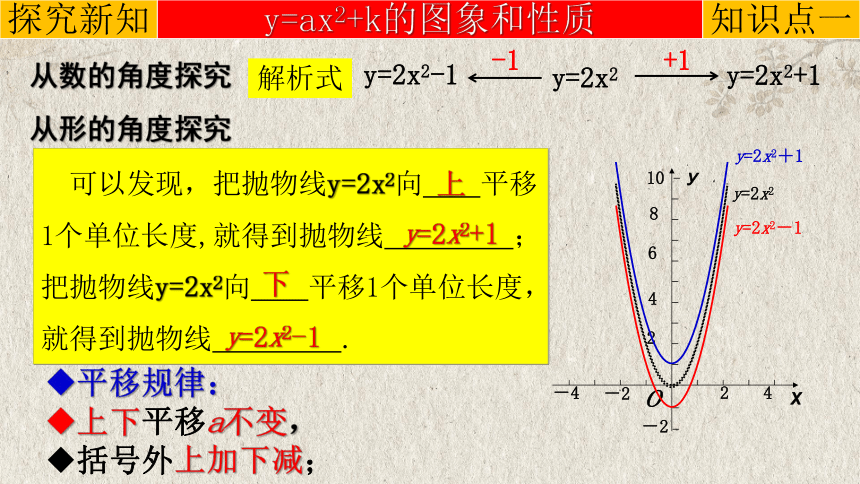
从数的角度探究
可以发现,把抛物线y=2x2向 平移1个单位长度,就得到抛物线 ;把抛物线y=2x2向 平移1个单位长度,就得到抛物线 .
下
y=2x2+1
上
从形的角度探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y=2x2+1
y=2x2-1
y=2x2
y=2x2-1
平移规律:
上下平移a不变,
括号外上加下减;
知识点一
探究新知
y=ax2+k的图象和性质
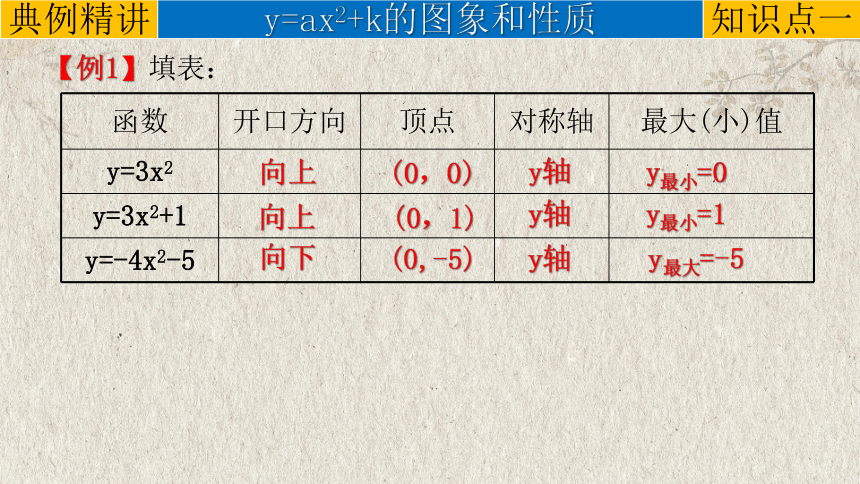
【例1】填表:
函数 开口方向 顶点 对称轴 最大(小)值
y=3x2
y=3x2+1
y=-4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y轴
y轴
y轴
y最小=0
y最小=1
y最大=-5
知识点一
典例精讲
y=ax2+k的图象和性质
1.抛物线y=-x2+3的顶点坐标是( )
A.(0,3) B.(0,-3) C.(3,0) D.(-3,0)
2.抛物线y=-x2-1的开口方向和对称轴分别是( )
A.向上,y轴 B.向下,y轴 C.向上,直线x=-1 D.向下,直线x=-1
B
A
知识点一
当堂训练
y=ax2+k的图象和性质
y=ax2+k的图象和性质
01
y=a(x-h)2的图象和性质
02
y=a(x-h)2+k的图象和性质
03
知识要点
精讲精练
O
x
1
2
3
–3
–2
–1
y
1
–1
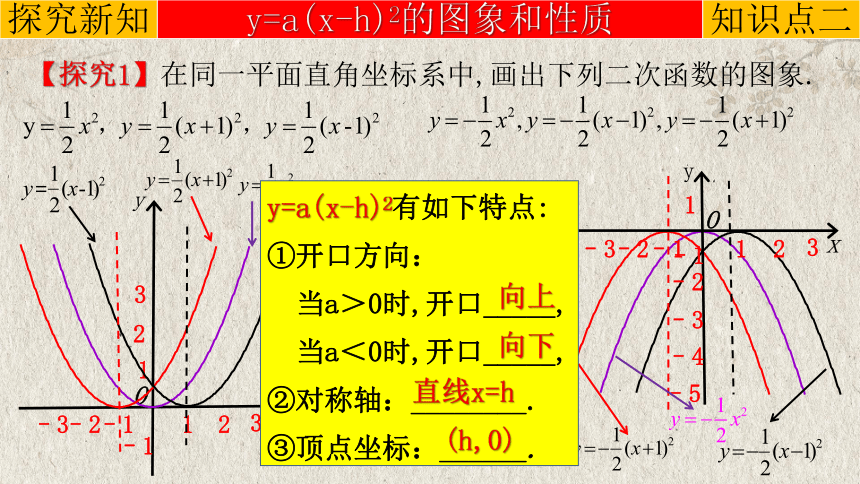
【探究1】在同一平面直角坐标系中,画出下列二次函数的图象.
3
2
O
x
1
2
3
–3
–2
–1
–5
–4
y
–3
–2
1
–1
y=a(x-h)2有如下特点:
①开口方向:
当a>0时,开口_____,
当a<0时,开口_____,
②对称轴:________.
③顶点坐标:______.
向上
向下
直线x=h
(h,0)
知识点二
探究新知
y=a(x-h)2的图象和性质
向右平移
1个单位
抛物线 , 与抛物线 有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
向左平移
1个单位
想一想
平移规律:
左右平移a不变,
括号内左加右减.
知识点二
探究新知
y=a(x-h)2的图象和性质
∴平移后二次函数关系式为y= (x-3)2.
【例2】抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
知识点二
典例精讲
y=a(x-h)2的图象和性质
指出下列函数图象的开口方向,对称轴和顶点坐标
二次函数 开口方向 对称轴 顶点坐标
y=2(x-3)2
y=-0.5(x+1)2
y=-3x2-1
y=2(x-2)2
y=0.5x2
y=-4x2-3
向上
直线x=3
(3,0)
向下
直线x=-1
(-1,0)
向下
直线x=0(y轴)
(0,-1)
向上
直线x=2
(2, 0)
向上
(0,0)
向下
(0,-3)
直线x=0(y轴)
直线x=0(y轴)
知识点二
当堂训练
y=a(x-h)2的图象和性质(口答竞赛)
y=ax2+k的图象和性质
01
y=a(x-h)2的图象和性质
02
y=a(x-h)2+k的图象和性质
03
知识要点
精讲精练
【问题1】画出函数 的图像.指出它的开口方向、顶点与对称轴
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
平移a不变.
1.上下平移,
括号外________;
2.左右平移,
括号内_________.
y=a(x-h)2+k有如下特点:
①开口方向:
当a>0时,开口_____,
当a<0时,开口_____,
②对称轴:________.
③顶点坐标:______.
向上
向下
直线x=h
(h,0)
上加下减
左加右减
知识点三
探究新知
y=a(x-h)2+k的图象和性质
【例1】已知二次函数y=2(x-3)2+1.下列对其图象的说法:
①开口向下; ②当x<3时,y随x的增大而减小;
③顶点坐标为(3,-1); ④对称轴为直线x=-3;
则其中说法正确的有( )A.1个 B.2个 C.3个 D.4个
A
知识点三
典例精讲
y=a(x-h)2+k的图象和性质
函数 开口方向 对称轴 顶点 最值 增减性
y=2(x-3)2+3
y=-2(x+3)2-2
y=-2(x-2)2-1
y=3(x+1)2+1
向上
x=3
(3,3)
3
x<3,y随x的增大而减小,
x>3,y随x的增大而增大.
向下
x=-3
(-3,-2)
-2
x>-3,y随x的增大而减小,
x<-3,y随x的增大而增大.
向下
x=2
(2,-1)
-1
x>2,y随x的增大而减小,
x<2,y随x的增大而增大.
向上
x=-1
(-1,1)
1
x<-1,y随x的增大而减小,
x>-1,y随x的增大而增大.
知识点三
当堂训练
y=a(x-h)2+k的图象和性质
2.画出下列函数图象(草图),并说出抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?
(1)y=2(x-3)2+3 (2)y=-2(x+3)2-2
(3)y=-2(x-2)2-1 (4)y=3(x+1)2+1
知识点三
当堂训练
y=a(x-h)2+k的图象和性质
y=a(x-h)2+k a>0 a<0
开口 方向
大小 顶点坐标 对 称 轴 最 值 增 减 性
平移规律 向上
向下
(h,k)
x=h
x=h时,y最值=k
|a|越大,开口越小
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
左右平移:括号内左加右减;
上下平移:括号外上加下减.
知识梳理
课堂小结
二次函数y=a(x-h)2+k的图象和性质
强
化
训
练
1.在同一坐标平面内,图象可能由函数y=2x2+1的图象通过平移变换得到的函数是( )
A.y=2x-5 B.y=0.5x2+3 C.y=3x2-10 D.y=3+2x2
2.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________.
3.抛物线y=3x2-4、抛物线y=3(x-1)2与抛物线y=3x2的形状_____,位置_____.
抛物线y=3x2-4是由抛物线y=3x2向___平移___个单位而得到;
抛物线y=3(x-1)2是由抛物线y=3x2向____平移____单位而得到.
D
查漏补缺
巩固训练
二次函数y=a(x-h)2+k的图象和性质
y=-3(x-2)2+3
相同
不同
下
4
右
1
4.函数y=-2(x+1)2的图象开口向___,对称轴是_________,顶点坐标是_______,
当x_____时,函数有最____值为___;
当x_____时,y随x的增大而增大,
当x_____时,y随x的增大而减小。
5.若y=x2+(k-2)的顶点是原点,则k____;
若顶点位于x轴上方,则k____;
若顶点位于x轴下方,则k .
=2
>2
<2
下
直线x=-1
(-1,0)
=-1
大
0
<-1
>-1
查漏补缺
巩固训练
二次函数y=a(x-h)2+k的图象和性质
1.已知二次函数y=a(x+1)2-b有最小值1,则a,b的大小关系为( )
A.a>b B.a<b C.a=b D.不能确定
A
提升能力
强化训练
二次函数的图象及性质
人教版九年级(上)数学教学课件
第22章 二次函数
22.1 二次函数的图象和性质
情境导入
探究新知
当堂训练
典例精讲
知识归纳
22.1.3 二次函数y=a(x-h)2+k的图象和性质
情境导入
温故知新
二次函数的图像和性质
已知二次函数①y=-x2;②y= x2;③y=15x2;④y=-4x2;
⑤y= x2;⑥y=4x2.
(1)其中开口向上的有 (填题号);
(2)其中开口向下,且开口最大的是 (填题号);
(3)当自变量由小到大变化时,函数值先逐渐变大,然后逐渐变小的有 (填题号).
②③⑥
⑤
①④⑤
y=ax2+k的图象和性质
01
y=a(x-h)2的图象和性质
02
y=a(x-h)2+k的图象和性质
03
知识要点
精讲精练
【问题】在同一平面直角坐标系中,画出下列二次函数的图象.
y=2x2+1
10
8
6
4
2
-2
-3
3
x
y
y=2x2-1
y=2x2
O
y=2x2,y=2x2+1,y=2x2-1
2
-2
-4
-6
-8
-10
-3
3
x
y
O
y=ax2+k有如下特点:
①开口方向:
当a>0时,开口_____,
当a<0时,开口_____,
②对称轴:________.
③顶点坐标:______.
向上
向下
直线x=0
(0,k)
知识点一
探究新知
y=ax2+k的图象和性质
解析式
y=2x2
y=2x2+1
y=2x2-1
+1
-1
从数的角度探究
可以发现,把抛物线y=2x2向 平移1个单位长度,就得到抛物线 ;把抛物线y=2x2向 平移1个单位长度,就得到抛物线 .
下
y=2x2+1
上
从形的角度探究
4
x
y
O
-2
2
2
4
6
-4
8
10
-2
y=2x2+1
y=2x2-1
y=2x2
y=2x2-1
平移规律:
上下平移a不变,
括号外上加下减;
知识点一
探究新知
y=ax2+k的图象和性质
【例1】填表:
函数 开口方向 顶点 对称轴 最大(小)值
y=3x2
y=3x2+1
y=-4x2-5
向上
向上
向下
(0,0)
(0,1)
(0,-5)
y轴
y轴
y轴
y最小=0
y最小=1
y最大=-5
知识点一
典例精讲
y=ax2+k的图象和性质
1.抛物线y=-x2+3的顶点坐标是( )
A.(0,3) B.(0,-3) C.(3,0) D.(-3,0)
2.抛物线y=-x2-1的开口方向和对称轴分别是( )
A.向上,y轴 B.向下,y轴 C.向上,直线x=-1 D.向下,直线x=-1
B
A
知识点一
当堂训练
y=ax2+k的图象和性质
y=ax2+k的图象和性质
01
y=a(x-h)2的图象和性质
02
y=a(x-h)2+k的图象和性质
03
知识要点
精讲精练
O
x
1
2
3
–3
–2
–1
y
1
–1
【探究1】在同一平面直角坐标系中,画出下列二次函数的图象.
3
2
O
x
1
2
3
–3
–2
–1
–5
–4
y
–3
–2
1
–1
y=a(x-h)2有如下特点:
①开口方向:
当a>0时,开口_____,
当a<0时,开口_____,
②对称轴:________.
③顶点坐标:______.
向上
向下
直线x=h
(h,0)
知识点二
探究新知
y=a(x-h)2的图象和性质
向右平移
1个单位
抛物线 , 与抛物线 有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
向左平移
1个单位
想一想
平移规律:
左右平移a不变,
括号内左加右减.
知识点二
探究新知
y=a(x-h)2的图象和性质
∴平移后二次函数关系式为y= (x-3)2.
【例2】抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
知识点二
典例精讲
y=a(x-h)2的图象和性质
指出下列函数图象的开口方向,对称轴和顶点坐标
二次函数 开口方向 对称轴 顶点坐标
y=2(x-3)2
y=-0.5(x+1)2
y=-3x2-1
y=2(x-2)2
y=0.5x2
y=-4x2-3
向上
直线x=3
(3,0)
向下
直线x=-1
(-1,0)
向下
直线x=0(y轴)
(0,-1)
向上
直线x=2
(2, 0)
向上
(0,0)
向下
(0,-3)
直线x=0(y轴)
直线x=0(y轴)
知识点二
当堂训练
y=a(x-h)2的图象和性质(口答竞赛)
y=ax2+k的图象和性质
01
y=a(x-h)2的图象和性质
02
y=a(x-h)2+k的图象和性质
03
知识要点
精讲精练
【问题1】画出函数 的图像.指出它的开口方向、顶点与对称轴
1
2
3
4
5
x
-1
-2
-3
-4
-5
-6
-7
-8
-9
1
y
o
-1
-2
-3
-4
-5
-10
平移a不变.
1.上下平移,
括号外________;
2.左右平移,
括号内_________.
y=a(x-h)2+k有如下特点:
①开口方向:
当a>0时,开口_____,
当a<0时,开口_____,
②对称轴:________.
③顶点坐标:______.
向上
向下
直线x=h
(h,0)
上加下减
左加右减
知识点三
探究新知
y=a(x-h)2+k的图象和性质
【例1】已知二次函数y=2(x-3)2+1.下列对其图象的说法:
①开口向下; ②当x<3时,y随x的增大而减小;
③顶点坐标为(3,-1); ④对称轴为直线x=-3;
则其中说法正确的有( )A.1个 B.2个 C.3个 D.4个
A
知识点三
典例精讲
y=a(x-h)2+k的图象和性质
函数 开口方向 对称轴 顶点 最值 增减性
y=2(x-3)2+3
y=-2(x+3)2-2
y=-2(x-2)2-1
y=3(x+1)2+1
向上
x=3
(3,3)
3
x<3,y随x的增大而减小,
x>3,y随x的增大而增大.
向下
x=-3
(-3,-2)
-2
x>-3,y随x的增大而减小,
x<-3,y随x的增大而增大.
向下
x=2
(2,-1)
-1
x>2,y随x的增大而减小,
x<2,y随x的增大而增大.
向上
x=-1
(-1,1)
1
x<-1,y随x的增大而减小,
x>-1,y随x的增大而增大.
知识点三
当堂训练
y=a(x-h)2+k的图象和性质
2.画出下列函数图象(草图),并说出抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?
(1)y=2(x-3)2+3 (2)y=-2(x+3)2-2
(3)y=-2(x-2)2-1 (4)y=3(x+1)2+1
知识点三
当堂训练
y=a(x-h)2+k的图象和性质
y=a(x-h)2+k a>0 a<0
开口 方向
大小 顶点坐标 对 称 轴 最 值 增 减 性
平移规律 向上
向下
(h,k)
x=h
x=h时,y最值=k
|a|越大,开口越小
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
左右平移:括号内左加右减;
上下平移:括号外上加下减.
知识梳理
课堂小结
二次函数y=a(x-h)2+k的图象和性质
强
化
训
练
1.在同一坐标平面内,图象可能由函数y=2x2+1的图象通过平移变换得到的函数是( )
A.y=2x-5 B.y=0.5x2+3 C.y=3x2-10 D.y=3+2x2
2.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________.
3.抛物线y=3x2-4、抛物线y=3(x-1)2与抛物线y=3x2的形状_____,位置_____.
抛物线y=3x2-4是由抛物线y=3x2向___平移___个单位而得到;
抛物线y=3(x-1)2是由抛物线y=3x2向____平移____单位而得到.
D
查漏补缺
巩固训练
二次函数y=a(x-h)2+k的图象和性质
y=-3(x-2)2+3
相同
不同
下
4
右
1
4.函数y=-2(x+1)2的图象开口向___,对称轴是_________,顶点坐标是_______,
当x_____时,函数有最____值为___;
当x_____时,y随x的增大而增大,
当x_____时,y随x的增大而减小。
5.若y=x2+(k-2)的顶点是原点,则k____;
若顶点位于x轴上方,则k____;
若顶点位于x轴下方,则k .
=2
>2
<2
下
直线x=-1
(-1,0)
=-1
大
0
<-1
>-1
查漏补缺
巩固训练
二次函数y=a(x-h)2+k的图象和性质
1.已知二次函数y=a(x+1)2-b有最小值1,则a,b的大小关系为( )
A.a>b B.a<b C.a=b D.不能确定
A
提升能力
强化训练
二次函数的图象及性质
同课章节目录
