华东师大版九年级数学上册23.3相似三角形 同步测试题(含解析)
文档属性
| 名称 | 华东师大版九年级数学上册23.3相似三角形 同步测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 349.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 10:13:34 | ||
图片预览

文档简介
2022-2023学年华东师大版九年级数学上册《23.3相似三角形》同步测试题(附答案)
一.选择题(共12小题,满分48分)
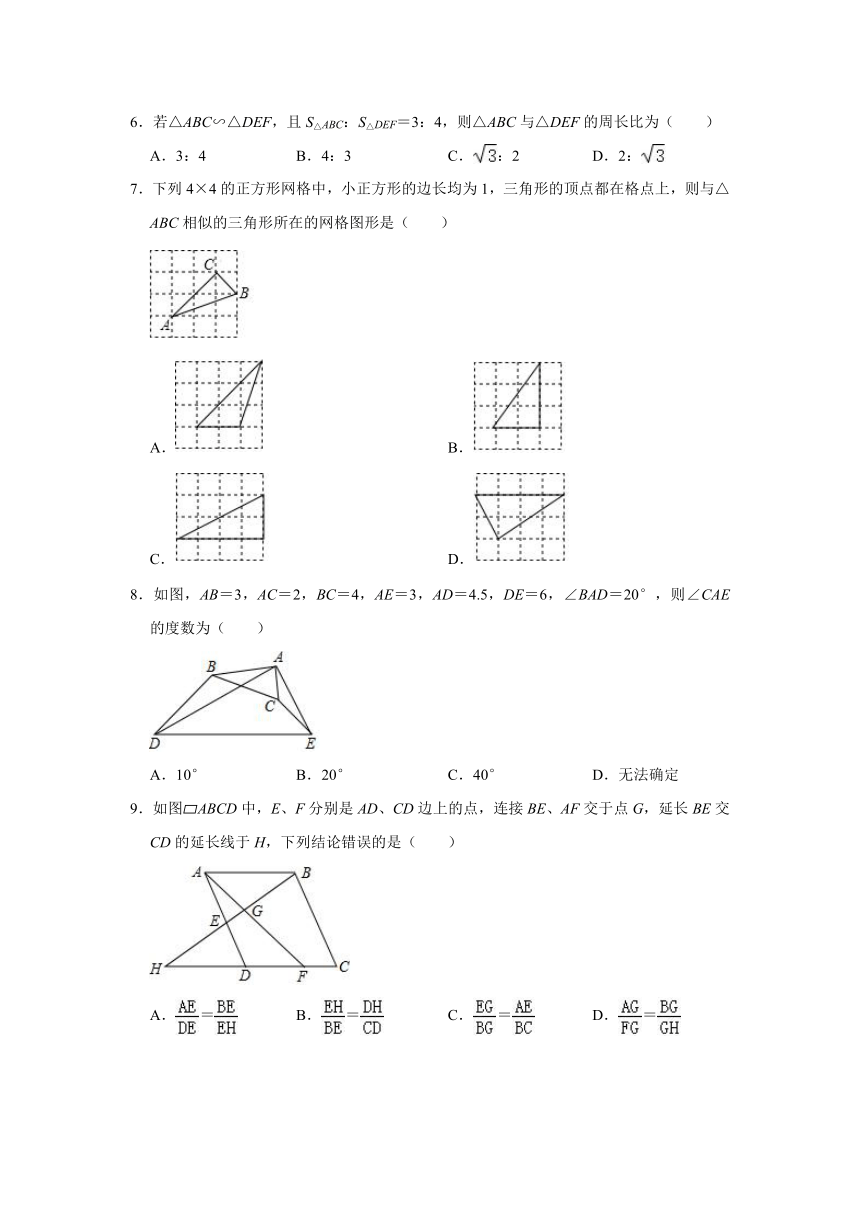
1.下列判断中,不正确的有( )
A.三边对应成比例的两个三角形相似
B.两边对应成比例,且有一个角相等的两个三角形相似
C.斜边与一条直角边对应成比例的两个直角三角形相似
D.有一个角是100°的两个等腰三角形相似
2.如图,在矩形ABCD中,点E是边BC的中点,则S△BEF:S△ADF=( )
A.1:2 B.2:3 C.1:3 D.1:4
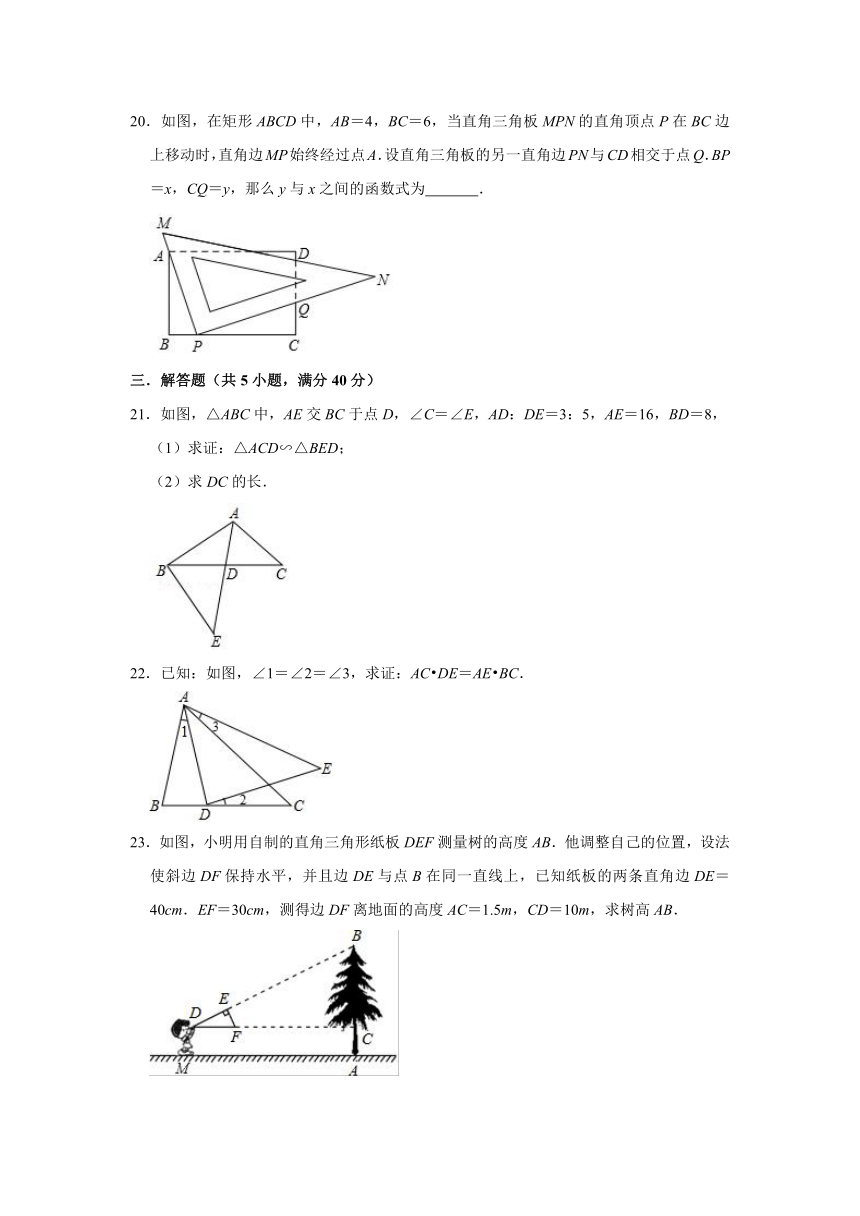
3.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=,能其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
4.如图,在矩形ABCD中,AB=3,BC=4,点M在BC边上,且满足BM=1,过D作DN⊥AM交AM于点N,则DN的长为( )
A. B. C. D.
5.如图,在△ABC中,点D在线段BC上,∠B=∠DAC,AC=8,BC=16,那么CD( )
A.4 B.6 C.8 D.10
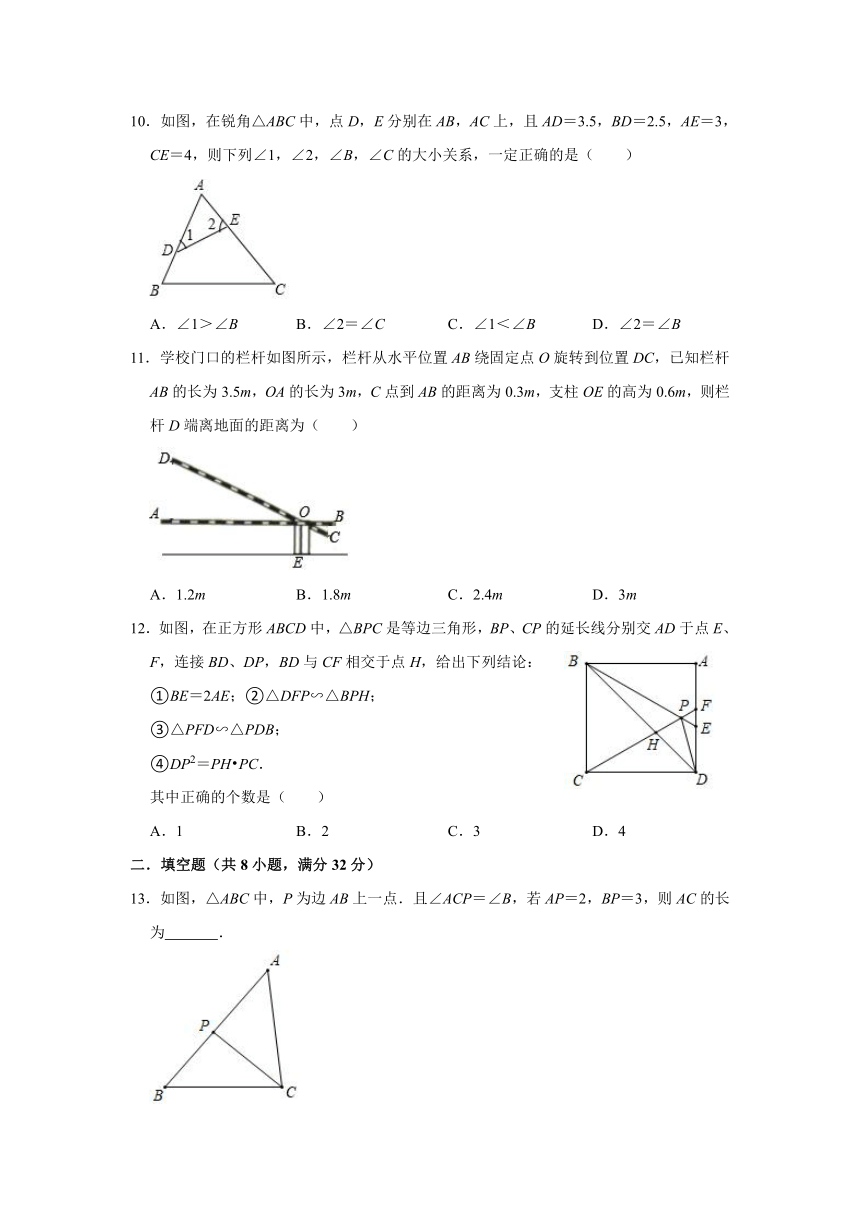
6.若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为( )
A.3:4 B.4:3 C.:2 D.2:
7.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A. B.
C. D.
8.如图,AB=3,AC=2,BC=4,AE=3,AD=4.5,DE=6,∠BAD=20°,则∠CAE的度数为( )
A.10° B.20° C.40° D.无法确定
9.如图 ABCD中,E、F分别是AD、CD边上的点,连接BE、AF交于点G,延长BE交CD的延长线于H,下列结论错误的是( )
A.= B.= C.= D.=
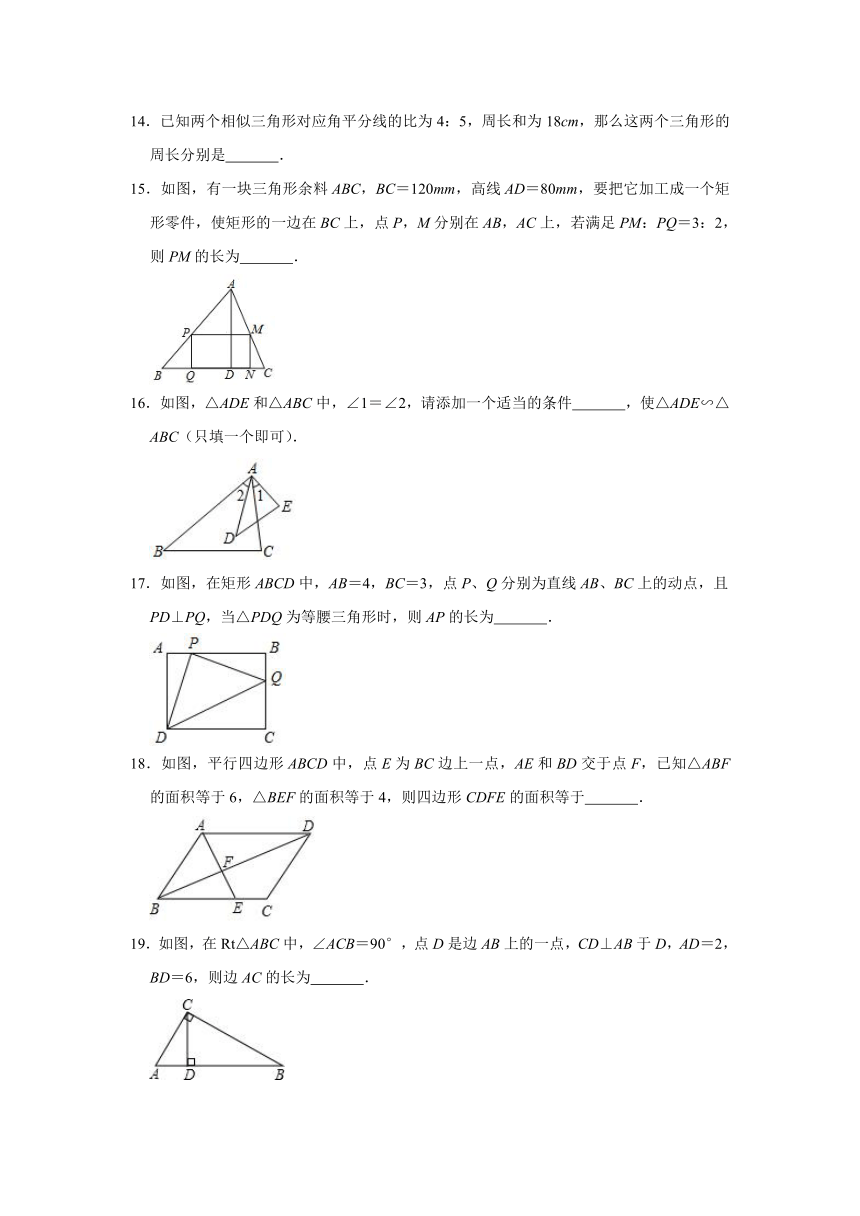
10.如图,在锐角△ABC中,点D,E分别在AB,AC上,且AD=3.5,BD=2.5,AE=3,CE=4,则下列∠1,∠2,∠B,∠C的大小关系,一定正确的是( )
A.∠1>∠B B.∠2=∠C C.∠1<∠B D.∠2=∠B
11.学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5m,OA的长为3m,C点到AB的距离为0.3m,支柱OE的高为0.6m,则栏杆D端离地面的距离为( )
A.1.2m B.1.8m C.2.4m D.3m
12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;
③△PFD∽△PDB;
④DP2=PH PC.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共8小题,满分32分)
13.如图,△ABC中,P为边AB上一点.且∠ACP=∠B,若AP=2,BP=3,则AC的长为 .
14.已知两个相似三角形对应角平分线的比为4:5,周长和为18cm,那么这两个三角形的周长分别是 .
15.如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为 .
16.如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件 ,使△ADE∽△ABC(只填一个即可).
17.如图,在矩形ABCD中,AB=4,BC=3,点P、Q分别为直线AB、BC上的动点,且PD⊥PQ,当△PDQ为等腰三角形时,则AP的长为 .
18.如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于6,△BEF的面积等于4,则四边形CDFE的面积等于 .
19.如图,在Rt△ABC中,∠ACB=90°,点D是边AB上的一点,CD⊥AB于D,AD=2,BD=6,则边AC的长为 .
20.如图,在矩形ABCD中,AB=4,BC=6,当直角三角板MPN的直角顶点P在BC边上移动时,直角边MP始终经过点A.设直角三角板的另一直角边PN与CD相交于点Q.BP=x,CQ=y,那么y与x之间的函数式为 .
三.解答题(共5小题,满分40分)
21.如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=16,BD=8,
(1)求证:△ACD∽△BED;
(2)求DC的长.
22.已知:如图,∠1=∠2=∠3,求证:AC DE=AE BC.
23.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
24.在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB>AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
25.如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)当t=2时,求点E的坐标;
(2)若AB平分∠EBP时,求t的值;
(3)在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一.选择题(共12小题,满分48分)
1.解:A、三边对应成比例的两个三角形相似,故A选项不合题意;
B、两边对应成比例,且夹角相等的两个三角形相似,故B选项符合题意;
C、斜边与一条直角边对应成比例的两个直角三角形相似,故C选项不合题意;
D、有一个角是100°的两个等腰三角形,则它们的底角都是40°,所以有一个角是100°的两个等腰三角形相似,故D选项不合题意;
故选:B.
2.解:∵点E是边BC的中点,
∴BE=BC,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴BE=AD,△BEF∽△DAF,
∴S△BEF:S△ADF=()2==1:4;
故选:D.
3.解:∵MN∥BC,
∴=,=,故①错误,③正确;
∵DN∥MC,
∴,=,故④正确;
∴=,故②正确,
故选:C.
4.解:连接DM,如图所示:
∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=4,△AMD底边AD上的高为AB,
AM===,
∵△ADM的面积=AM×DN=AD×AB,
∴DN===;
故选:D.
5.解:∵∠B=∠DAC,∠C=∠C,
∴△ABC∽△DAC,
∴=,
∴AC2=CD×BC,即82=CD×16,
解得:CD=4;
故选:A.
6.解:∵△ABC∽△DEF,S△ABC:S△DEF=3:4,
∴△ABC与△DEF的相似比为::2,
∴△ABC与△DEF的周长比为::2.故选:C.
7.解:根据勾股定理,AC==2,BC=,
所以,夹直角的两边的比为=2,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.故选:C.
8.解:=,==,==,
∴==,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠CAE=∠BAD=20°,故选:B.
9.解:∵四边形ABCD是平行四边形,
∴AB∥CH,AB=CD,
∴△ABE∽△DHE,△ABG∽△FHG,
∴=,==,=,
故选项A,B,D正确,故选:C.
10.解:∵AD=3.5,BD=2.5,AE=3,CE=4,
∴AB=6,
AC=7,
∴==,==,
∴=,
∵∠A=∠A,
∴△ADE∽△ACB,
∴∠2=∠B,∠1=∠C,
故选:D.
11.解:过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG∥CH,
∴△ODG∽△OCH,
∴=,
∵栏杆从水平位置AB绕固定点O旋转到位置DC,
∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴OC=0.5m,
∴=,
∴DG=1.8m,
∵OE=0.6m,
∴栏杆D端离地面的距离为1.8+0.6=2.4m. 故选:C.
12.解:∵四边形ABCD是正方形,
∴∠A=∠CBA=90°,
∵△BCP是等边三角形,
∴∠PBC=∠PCB=∠BPC=60°,
∴∠ABE=30°,
∴BE=2AE,故①正确,
∵AD∥BC,
∴∠DFP=∠BCP=∠BPH=60°,
∵∠PHB=∠PCB+∠CBH=60°+45°=105°,
又∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°,
∴∠DPF=105°,
∴∠PHB=∠DPF,
∴△DFP∽△BPH,故②正确,
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似,故③错误,
∵∠PDH=∠PDC﹣∠CDH=75°﹣45°=30°,
∴∠PDH=∠PCD,
∵∠DPH=∠CPD,
∴△PDH∽△PCD,
∴=,
∴PD2=PH PC,故④正确,故选:C.
二.填空题(共8小题,满分32分)
13.解:AB=AP+BP=2+3=5,
∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,
∴=,
∴AC2=AP AB=2×5=10,
∴AC=,
故答案为:.
14.解:设其中一个三角形的周长为xcm,则另一个三角形的周长为(18﹣x)cm,
∵两个相似三角形对应角平分线的比为4:5,
∴两个相似三角形的相似比为4:5,
∴两个相似三角形的周长比为4:5,
∴=,
解得,x=8,
则18﹣x=10,
故答案为:8cm、10cm.
15.解:如图,设AD交PN于点K.
∵PM:PQ=3:2,
∴可以假设MP=3k,PQ=2k.
∵四边形PQNM是矩形,
∴PM∥BC,
∴△APM∽△ABC,
∵AD⊥BC,BC∥PM,
∴AD⊥PN,
∴=,
∴=,
解得k=20mm,
∴PM=3k=60mm,
故答案为:60mm.
16.解:∵∠1=∠2,
∴∠DAE=∠BAC,
∴要使△ADE∽△ABC,则添加的一个条件可以是∠D=∠B或∠E=∠C或=.
故答案为:∠D=∠B或∠E=∠C或=.
17.解:当P点在边AB上,如图1,
∵四边形ABCD为矩形,
∴AD=BC=3,∠A=∠B=90°,
∵PD⊥PQ,
∴∠DPQ=90°,
∵∠APD+∠ADP=90°,∠APD+∠BPQ=90°,
∴∠ADP=∠BPQ,
∴Rt△ADP∽Rt△BPQ,
∴==1,
∴PB=AD=3,
∴AP=AB﹣PB=4﹣3=1.
当P点在AB的延长线上时,如图2,
同样方法得到Rt△ADP∽Rt△BPQ,
∴==1,
∴PB=AD=3,
∴AP=AB+PB=4+3=7.
综上所述,AP的长度为1或7. 故答案为1或7.
18.解:∵△ABF的面积等于6,△BEF的面积等于4,
即S△ABF:S△BEF=6:4=3:2,
∴AF:FE=3:2,
∵四边形ABCD为平行四边形,
∴AD∥BE,S△ABD=S△CBD,
∴△AFD∽△EFB,
∴=()2=()2=,
∴S△AFD=×4=9,
∴S△ABD=S△CBD=6+9=15,
∴四边形CDFE的面积=15﹣4=11.
故答案为11.
19.解:由射影定理得,AC2=AD AB=2×(2+6),
解得,AC=4,
故答案为:4.
20.解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,∵∠APQ=90°,
∴∠APB+∠QPC=90°,∠QPC+∠PQC=90°,
∴∠APB=∠PQC,
∴△ABP∽△PCQ,
∴=,
∴=,
∴y=﹣x2+x(0<x<6),
故答案为:y=﹣x2+x(0<x<6).
三.解答题(共5小题,满分40分)
21.解:(1)∵∠C=∠E,∠ADC=∠BDE,
∴△ACD∽△BED;
(2)∵△ACD∽△BED,
∴=,
又∵AD:DE=3:5,AE=16,
∴AD=6,DE=10,
∵BD=8,
∴=,即=.
∴DC=.
22.证明:∵∠1=∠2=∠3,
∴∠BAC=∠DAE,
∵∠ADC=∠ABC+∠1=∠ADE+∠2,
∴∠ADE=∠ABC,且∠BAC=∠DAE,
∴△ADE∽△ABC
∴
∴AC DE=AE BC.
23.解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米.
24.解:(1)CF与BD位置关系是垂直;
证明如下:
∵AB=AC,∠ACB=45°,
∴∠ABC=45°.
由正方形ADEF得AD=AF,
∵∠DAF=∠BAC=90°,
∴∠DAB=∠FAC,
∴△DAB≌△FAC(SAS),
∴∠ACF=∠ABD.
∴∠BCF=∠ACB+∠ACF=90°.
∴CF⊥BC.
∴CF⊥BD.
(2)AB>AC时,CF⊥BD的结论成立.
理由是:
过点A作GA⊥AC交BC于点G,
∵∠ACB=45°,
∴∠AGD=45°,
∴AC=AG,
同理可证:△GAD≌△CAF
∴∠ACF=∠AGD=45°,∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD.
(3)过点A作AQ⊥BC交CB的延长线于点Q,
①点D在线段BC上运动时,
∵∠BCA=45°,可求出AQ=CQ=4.
∴DQ=4﹣x,△AQD∽△DCP,
∴,
∴,
∴.
②点D在线段BC延长线上运动时,
∵∠BCA=45°,
∴AQ=CQ=4,
∴DQ=4+x.
过A作AQ⊥BC,
∴∠Q=∠FAD=90°,
∵∠C′AF=∠C′CD=90°,∠AC′F=∠CC′D,
∴∠ADQ=∠AFC′,
则△AQD∽△AC′F.
∴CF⊥BD,
∴△AQD∽△DCP,
∴,
∴,
∴.
25.解:(1)当t=2时,PC=2,
∵BC=2,
∴PC=BC,
∴∠PBC=45°,
∴∠BAE=90°,
∴∠AEB=45°,
∴AB=AE=3,
,
∴点E的坐标是(5,0);
(2)当AB平分∠EBP时,
∠PBF=45°,
则∠CBP=∠CPB=45°,
,
∴t=2;
(3)存在,
∵∠ABE+∠ABP=90°,
∠PBC+∠ABP=90°,
∴∠ABE=∠PBC,
∵∠BAE=∠BCP=90°,
∴△BCP∽△BAE,
∴,
∴,
∴,
当点P在点O上方时,
若=时,△POE∽△EAB,
∵OP=3﹣t,OE=2+t,
∴=,
∴t1=,
t2=(舍去),
∴OP=3﹣=,
∴P的坐标为(0,),
当点P在点O下方时,
①若=,
则△OPE∽△ABE,
=,
解得:t1=3+,t2=3﹣(舍去),
OP=t﹣3=3+﹣3=,
P的坐标为(0,﹣),
②若=,
则△OEP∽△ABE,=,
解得:t2=﹣9,
∴这种情况不成立,
∴P的坐标为:
(0,),(0,﹣).
一.选择题(共12小题,满分48分)
1.下列判断中,不正确的有( )
A.三边对应成比例的两个三角形相似
B.两边对应成比例,且有一个角相等的两个三角形相似
C.斜边与一条直角边对应成比例的两个直角三角形相似
D.有一个角是100°的两个等腰三角形相似
2.如图,在矩形ABCD中,点E是边BC的中点,则S△BEF:S△ADF=( )
A.1:2 B.2:3 C.1:3 D.1:4
3.如图,在△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:①=;②=;③=;④=,能其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
4.如图,在矩形ABCD中,AB=3,BC=4,点M在BC边上,且满足BM=1,过D作DN⊥AM交AM于点N,则DN的长为( )
A. B. C. D.
5.如图,在△ABC中,点D在线段BC上,∠B=∠DAC,AC=8,BC=16,那么CD( )
A.4 B.6 C.8 D.10
6.若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为( )
A.3:4 B.4:3 C.:2 D.2:
7.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A. B.
C. D.
8.如图,AB=3,AC=2,BC=4,AE=3,AD=4.5,DE=6,∠BAD=20°,则∠CAE的度数为( )
A.10° B.20° C.40° D.无法确定
9.如图 ABCD中,E、F分别是AD、CD边上的点,连接BE、AF交于点G,延长BE交CD的延长线于H,下列结论错误的是( )
A.= B.= C.= D.=
10.如图,在锐角△ABC中,点D,E分别在AB,AC上,且AD=3.5,BD=2.5,AE=3,CE=4,则下列∠1,∠2,∠B,∠C的大小关系,一定正确的是( )
A.∠1>∠B B.∠2=∠C C.∠1<∠B D.∠2=∠B
11.学校门口的栏杆如图所示,栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5m,OA的长为3m,C点到AB的距离为0.3m,支柱OE的高为0.6m,则栏杆D端离地面的距离为( )
A.1.2m B.1.8m C.2.4m D.3m
12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
①BE=2AE;②△DFP∽△BPH;
③△PFD∽△PDB;
④DP2=PH PC.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共8小题,满分32分)
13.如图,△ABC中,P为边AB上一点.且∠ACP=∠B,若AP=2,BP=3,则AC的长为 .
14.已知两个相似三角形对应角平分线的比为4:5,周长和为18cm,那么这两个三角形的周长分别是 .
15.如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为 .
16.如图,△ADE和△ABC中,∠1=∠2,请添加一个适当的条件 ,使△ADE∽△ABC(只填一个即可).
17.如图,在矩形ABCD中,AB=4,BC=3,点P、Q分别为直线AB、BC上的动点,且PD⊥PQ,当△PDQ为等腰三角形时,则AP的长为 .
18.如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于6,△BEF的面积等于4,则四边形CDFE的面积等于 .
19.如图,在Rt△ABC中,∠ACB=90°,点D是边AB上的一点,CD⊥AB于D,AD=2,BD=6,则边AC的长为 .
20.如图,在矩形ABCD中,AB=4,BC=6,当直角三角板MPN的直角顶点P在BC边上移动时,直角边MP始终经过点A.设直角三角板的另一直角边PN与CD相交于点Q.BP=x,CQ=y,那么y与x之间的函数式为 .
三.解答题(共5小题,满分40分)
21.如图,△ABC中,AE交BC于点D,∠C=∠E,AD:DE=3:5,AE=16,BD=8,
(1)求证:△ACD∽△BED;
(2)求DC的长.
22.已知:如图,∠1=∠2=∠3,求证:AC DE=AE BC.
23.如图,小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm.EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
24.在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB>AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
25.如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)当t=2时,求点E的坐标;
(2)若AB平分∠EBP时,求t的值;
(3)在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一.选择题(共12小题,满分48分)
1.解:A、三边对应成比例的两个三角形相似,故A选项不合题意;
B、两边对应成比例,且夹角相等的两个三角形相似,故B选项符合题意;
C、斜边与一条直角边对应成比例的两个直角三角形相似,故C选项不合题意;
D、有一个角是100°的两个等腰三角形,则它们的底角都是40°,所以有一个角是100°的两个等腰三角形相似,故D选项不合题意;
故选:B.
2.解:∵点E是边BC的中点,
∴BE=BC,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴BE=AD,△BEF∽△DAF,
∴S△BEF:S△ADF=()2==1:4;
故选:D.
3.解:∵MN∥BC,
∴=,=,故①错误,③正确;
∵DN∥MC,
∴,=,故④正确;
∴=,故②正确,
故选:C.
4.解:连接DM,如图所示:
∵四边形ABCD是矩形,
∴∠B=90°,AD=BC=4,△AMD底边AD上的高为AB,
AM===,
∵△ADM的面积=AM×DN=AD×AB,
∴DN===;
故选:D.
5.解:∵∠B=∠DAC,∠C=∠C,
∴△ABC∽△DAC,
∴=,
∴AC2=CD×BC,即82=CD×16,
解得:CD=4;
故选:A.
6.解:∵△ABC∽△DEF,S△ABC:S△DEF=3:4,
∴△ABC与△DEF的相似比为::2,
∴△ABC与△DEF的周长比为::2.故选:C.
7.解:根据勾股定理,AC==2,BC=,
所以,夹直角的两边的比为=2,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.故选:C.
8.解:=,==,==,
∴==,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠CAE=∠BAD=20°,故选:B.
9.解:∵四边形ABCD是平行四边形,
∴AB∥CH,AB=CD,
∴△ABE∽△DHE,△ABG∽△FHG,
∴=,==,=,
故选项A,B,D正确,故选:C.
10.解:∵AD=3.5,BD=2.5,AE=3,CE=4,
∴AB=6,
AC=7,
∴==,==,
∴=,
∵∠A=∠A,
∴△ADE∽△ACB,
∴∠2=∠B,∠1=∠C,
故选:D.
11.解:过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG∥CH,
∴△ODG∽△OCH,
∴=,
∵栏杆从水平位置AB绕固定点O旋转到位置DC,
∴CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴OC=0.5m,
∴=,
∴DG=1.8m,
∵OE=0.6m,
∴栏杆D端离地面的距离为1.8+0.6=2.4m. 故选:C.
12.解:∵四边形ABCD是正方形,
∴∠A=∠CBA=90°,
∵△BCP是等边三角形,
∴∠PBC=∠PCB=∠BPC=60°,
∴∠ABE=30°,
∴BE=2AE,故①正确,
∵AD∥BC,
∴∠DFP=∠BCP=∠BPH=60°,
∵∠PHB=∠PCB+∠CBH=60°+45°=105°,
又∵CD=CP,∠PCD=30°,
∴∠CPD=∠CDP=75°,
∴∠DPF=105°,
∴∠PHB=∠DPF,
∴△DFP∽△BPH,故②正确,
∵∠DPB=60°+75°=135°≠∠DPF,
∴△PFD与△PDB不相似,故③错误,
∵∠PDH=∠PDC﹣∠CDH=75°﹣45°=30°,
∴∠PDH=∠PCD,
∵∠DPH=∠CPD,
∴△PDH∽△PCD,
∴=,
∴PD2=PH PC,故④正确,故选:C.
二.填空题(共8小题,满分32分)
13.解:AB=AP+BP=2+3=5,
∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,
∴=,
∴AC2=AP AB=2×5=10,
∴AC=,
故答案为:.
14.解:设其中一个三角形的周长为xcm,则另一个三角形的周长为(18﹣x)cm,
∵两个相似三角形对应角平分线的比为4:5,
∴两个相似三角形的相似比为4:5,
∴两个相似三角形的周长比为4:5,
∴=,
解得,x=8,
则18﹣x=10,
故答案为:8cm、10cm.
15.解:如图,设AD交PN于点K.
∵PM:PQ=3:2,
∴可以假设MP=3k,PQ=2k.
∵四边形PQNM是矩形,
∴PM∥BC,
∴△APM∽△ABC,
∵AD⊥BC,BC∥PM,
∴AD⊥PN,
∴=,
∴=,
解得k=20mm,
∴PM=3k=60mm,
故答案为:60mm.
16.解:∵∠1=∠2,
∴∠DAE=∠BAC,
∴要使△ADE∽△ABC,则添加的一个条件可以是∠D=∠B或∠E=∠C或=.
故答案为:∠D=∠B或∠E=∠C或=.
17.解:当P点在边AB上,如图1,
∵四边形ABCD为矩形,
∴AD=BC=3,∠A=∠B=90°,
∵PD⊥PQ,
∴∠DPQ=90°,
∵∠APD+∠ADP=90°,∠APD+∠BPQ=90°,
∴∠ADP=∠BPQ,
∴Rt△ADP∽Rt△BPQ,
∴==1,
∴PB=AD=3,
∴AP=AB﹣PB=4﹣3=1.
当P点在AB的延长线上时,如图2,
同样方法得到Rt△ADP∽Rt△BPQ,
∴==1,
∴PB=AD=3,
∴AP=AB+PB=4+3=7.
综上所述,AP的长度为1或7. 故答案为1或7.
18.解:∵△ABF的面积等于6,△BEF的面积等于4,
即S△ABF:S△BEF=6:4=3:2,
∴AF:FE=3:2,
∵四边形ABCD为平行四边形,
∴AD∥BE,S△ABD=S△CBD,
∴△AFD∽△EFB,
∴=()2=()2=,
∴S△AFD=×4=9,
∴S△ABD=S△CBD=6+9=15,
∴四边形CDFE的面积=15﹣4=11.
故答案为11.
19.解:由射影定理得,AC2=AD AB=2×(2+6),
解得,AC=4,
故答案为:4.
20.解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,∵∠APQ=90°,
∴∠APB+∠QPC=90°,∠QPC+∠PQC=90°,
∴∠APB=∠PQC,
∴△ABP∽△PCQ,
∴=,
∴=,
∴y=﹣x2+x(0<x<6),
故答案为:y=﹣x2+x(0<x<6).
三.解答题(共5小题,满分40分)
21.解:(1)∵∠C=∠E,∠ADC=∠BDE,
∴△ACD∽△BED;
(2)∵△ACD∽△BED,
∴=,
又∵AD:DE=3:5,AE=16,
∴AD=6,DE=10,
∵BD=8,
∴=,即=.
∴DC=.
22.证明:∵∠1=∠2=∠3,
∴∠BAC=∠DAE,
∵∠ADC=∠ABC+∠1=∠ADE+∠2,
∴∠ADE=∠ABC,且∠BAC=∠DAE,
∴△ADE∽△ABC
∴
∴AC DE=AE BC.
23.解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴,
∵DE=40cm=0.4m,EF=30cm=0.3m,AC=1.5m,CD=10m,
∴,
∴BC=7.5米,
∴AB=AC+BC=1.5+7.5=9米.
24.解:(1)CF与BD位置关系是垂直;
证明如下:
∵AB=AC,∠ACB=45°,
∴∠ABC=45°.
由正方形ADEF得AD=AF,
∵∠DAF=∠BAC=90°,
∴∠DAB=∠FAC,
∴△DAB≌△FAC(SAS),
∴∠ACF=∠ABD.
∴∠BCF=∠ACB+∠ACF=90°.
∴CF⊥BC.
∴CF⊥BD.
(2)AB>AC时,CF⊥BD的结论成立.
理由是:
过点A作GA⊥AC交BC于点G,
∵∠ACB=45°,
∴∠AGD=45°,
∴AC=AG,
同理可证:△GAD≌△CAF
∴∠ACF=∠AGD=45°,∠BCF=∠ACB+∠ACF=90°,
即CF⊥BD.
(3)过点A作AQ⊥BC交CB的延长线于点Q,
①点D在线段BC上运动时,
∵∠BCA=45°,可求出AQ=CQ=4.
∴DQ=4﹣x,△AQD∽△DCP,
∴,
∴,
∴.
②点D在线段BC延长线上运动时,
∵∠BCA=45°,
∴AQ=CQ=4,
∴DQ=4+x.
过A作AQ⊥BC,
∴∠Q=∠FAD=90°,
∵∠C′AF=∠C′CD=90°,∠AC′F=∠CC′D,
∴∠ADQ=∠AFC′,
则△AQD∽△AC′F.
∴CF⊥BD,
∴△AQD∽△DCP,
∴,
∴,
∴.
25.解:(1)当t=2时,PC=2,
∵BC=2,
∴PC=BC,
∴∠PBC=45°,
∴∠BAE=90°,
∴∠AEB=45°,
∴AB=AE=3,
,
∴点E的坐标是(5,0);
(2)当AB平分∠EBP时,
∠PBF=45°,
则∠CBP=∠CPB=45°,
,
∴t=2;
(3)存在,
∵∠ABE+∠ABP=90°,
∠PBC+∠ABP=90°,
∴∠ABE=∠PBC,
∵∠BAE=∠BCP=90°,
∴△BCP∽△BAE,
∴,
∴,
∴,
当点P在点O上方时,
若=时,△POE∽△EAB,
∵OP=3﹣t,OE=2+t,
∴=,
∴t1=,
t2=(舍去),
∴OP=3﹣=,
∴P的坐标为(0,),
当点P在点O下方时,
①若=,
则△OPE∽△ABE,
=,
解得:t1=3+,t2=3﹣(舍去),
OP=t﹣3=3+﹣3=,
P的坐标为(0,﹣),
②若=,
则△OEP∽△ABE,=,
解得:t2=﹣9,
∴这种情况不成立,
∴P的坐标为:
(0,),(0,﹣).
