13.2.2 等边三角形课件
文档属性
| 名称 | 13.2.2 等边三角形课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 67.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-19 00:00:00 | ||
图片预览



文档简介
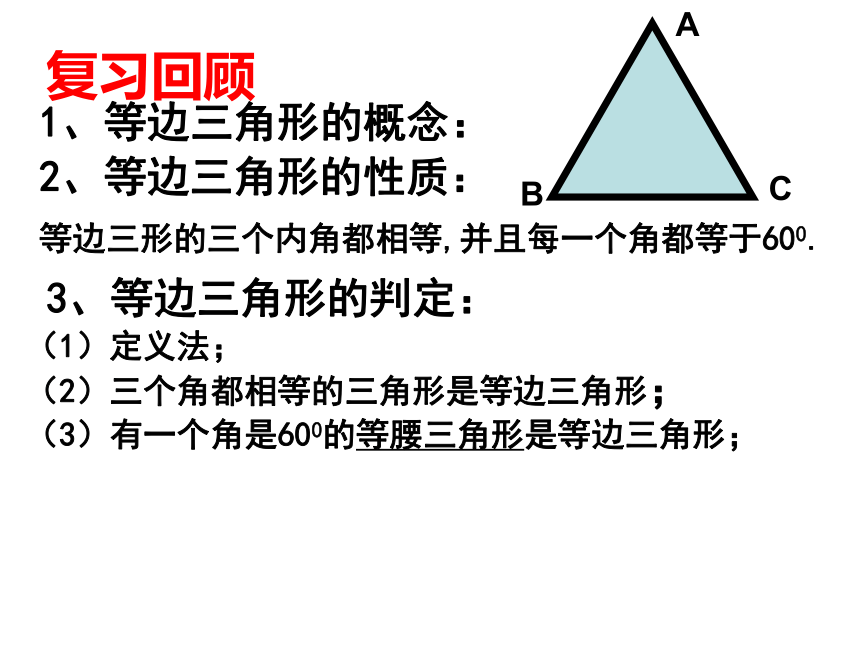
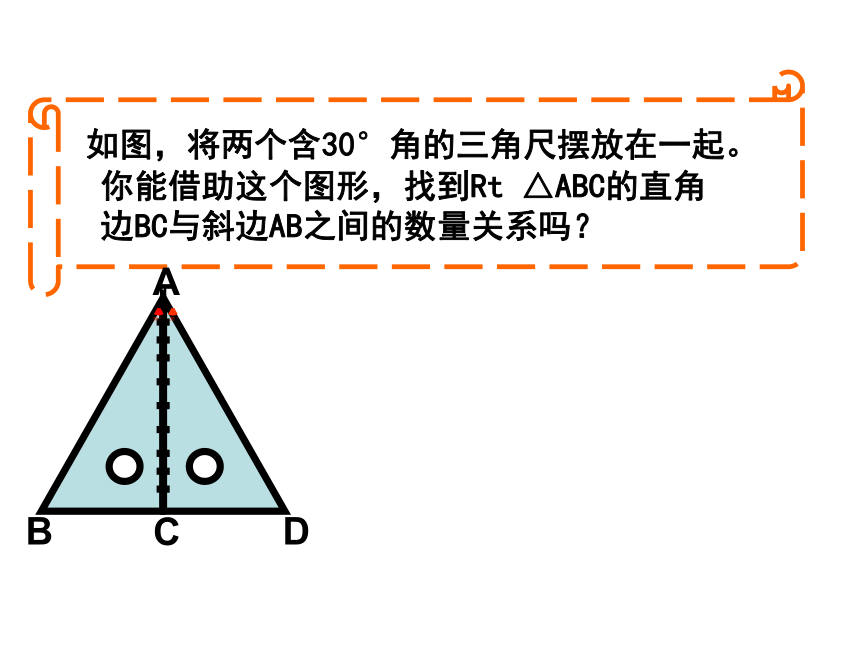
课件16张PPT。复习回顾1、等边三角形的概念:2、等边三角形的性质:3、等边三角形的判定:等边三形的三个内角都相等,并且每一个角都等于600.(1)定义法;(2)三个角都相等的三角形是等边三角形;(3)有一个角是600的等腰三角形是等边三角形; 如图,将两个含30°角的三角尺摆放在一起。
你能借助这个图形,找到Rt △ABC的直角
边BC与斜边AB之间的数量关系吗?13.3.2 等边三角形(2)学习目标:
1、弄清含有30°角的直角三角形的性质;
2、会用含有30°角的直角三角形的性质解决有关问题.
重点:含有30°角的直角三角形的性质.
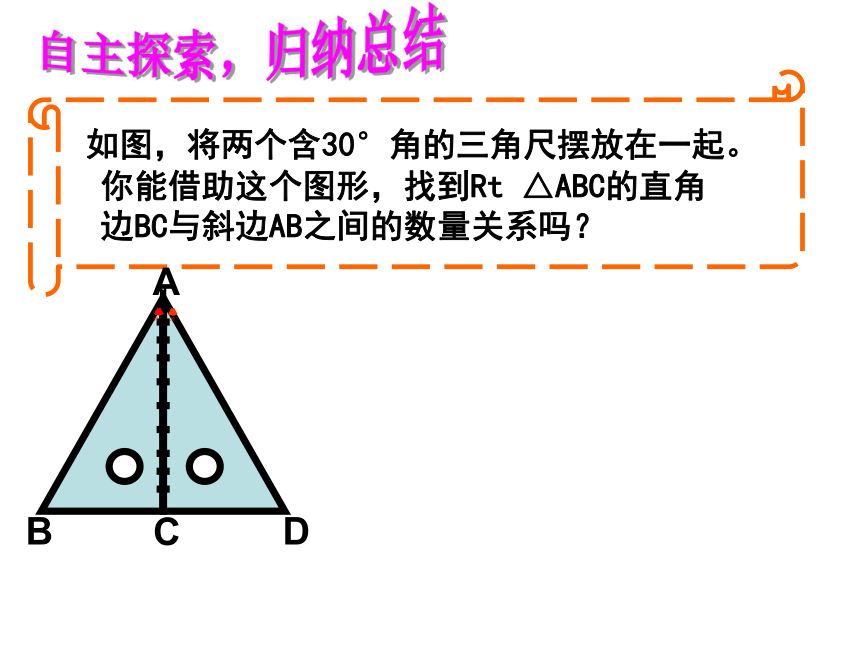
难点:含有30°角的直角三角形的性质的运用. 如图,将两个含30°角的三角尺摆放在一起。
你能借助这个图形,找到Rt △ABC的直角
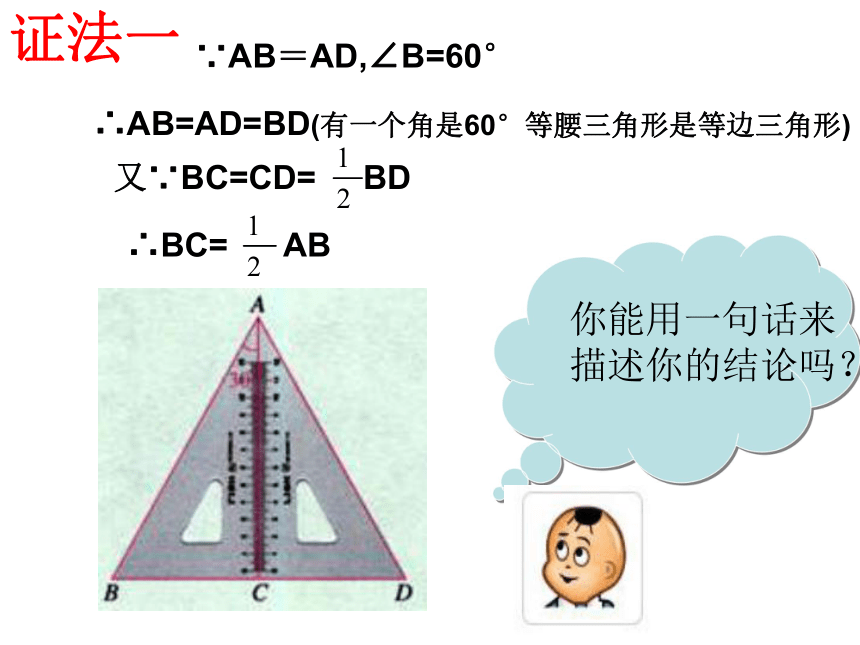
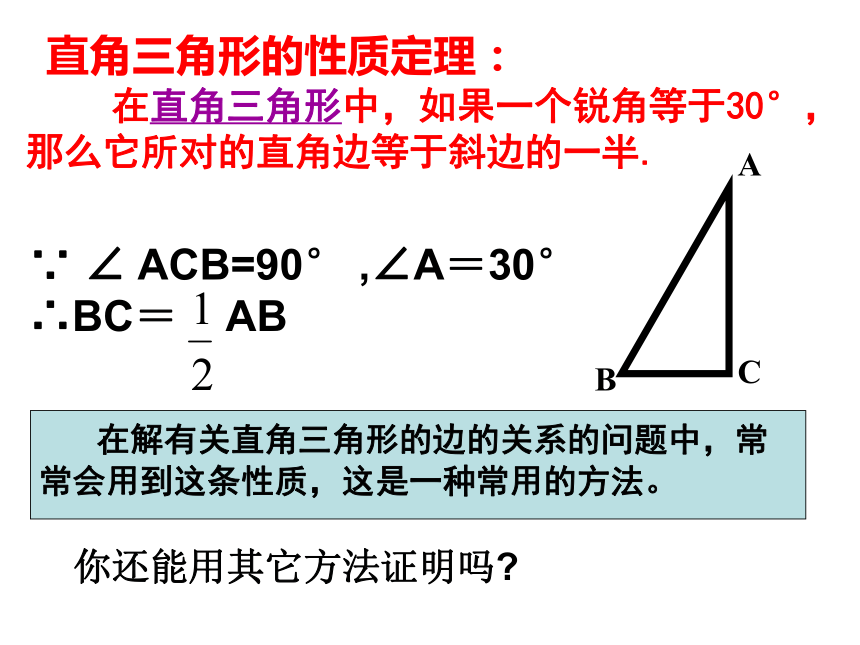
边BC与斜边AB之间的数量关系吗?自主探索,归纳总结∵AB=AD,∠B=60°∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形)又∵BC=CD= BD∴BC= AB证法一直角三角形的性质定理: 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 在解有关直角三角形的边的关系的问题中,常常会用到这条性质,这是一种常用的方法。你还能用其它方法证明吗?另证:在BA上截取BE=BC,连接EC
则△BCE是等边三角形,所以
∠BEC= 60°,而∠A= 30°,
所以∠ECA= 30°,
所以AE=EC,于是有
BC= AB比一比:看 谁 算 的 快1.如图:在Rt△ABC中
∠A=300,AB=12cm
则BC=_____cm62.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,
BD=___, BE=_______4cm 2cm应用新知,巩固提高 例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC 、 DE要多长?解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又AD=1/2AB,
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.1、如图,在Rt△ABC中, ∠B=2 ∠A,AB=6cm,则BC=________.2、如图, Rt△ABC中, ∠A= 30°,AB+BC=12cm,则AB= _______.3cm8cm3、如图, Rt△ABC中, ∠A= 30°,BD
平分∠ABC,且BD=16cm,则AC= .D24cmAD=2CD成立吗?练一练4、如图,在△ABC中, ∠ACB= 90°,BA的
垂直平分线交边CB于D。若AB=10,AC=5,
则图中等于 30°的角的个数为( )A.2 B.3
C.4 D.5B5、如图,在△ABC中, AB=AC,
∠BAC= 120°,AC的垂直平分线EF交AC
于点E,交BC于点F。求证:BF=2CF6、如图,上午9时,一条渔船从A出发,以12海里/时的速度向正北航行,11时到达B处,从A、B两处望小岛C,测得∠NAC=150, ∠NBC=300,若小岛周围12.3海里内有暗礁,问该渔船继续向正北航行有无触礁的危险?NABCD经过本节课的学习,你有哪些收获?共同回顾 如图,在△ABC中, ∠ACB= 90°,
∠B= 15°,AB的垂直平分线分别交BC、AB
于D、E。求证:DB=2ACBEDAC当堂检测,自我评价
你能借助这个图形,找到Rt △ABC的直角
边BC与斜边AB之间的数量关系吗?13.3.2 等边三角形(2)学习目标:
1、弄清含有30°角的直角三角形的性质;
2、会用含有30°角的直角三角形的性质解决有关问题.
重点:含有30°角的直角三角形的性质.
难点:含有30°角的直角三角形的性质的运用. 如图,将两个含30°角的三角尺摆放在一起。
你能借助这个图形,找到Rt △ABC的直角
边BC与斜边AB之间的数量关系吗?自主探索,归纳总结∵AB=AD,∠B=60°∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形)又∵BC=CD= BD∴BC= AB证法一直角三角形的性质定理: 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 在解有关直角三角形的边的关系的问题中,常常会用到这条性质,这是一种常用的方法。你还能用其它方法证明吗?另证:在BA上截取BE=BC,连接EC
则△BCE是等边三角形,所以
∠BEC= 60°,而∠A= 30°,
所以∠ECA= 30°,
所以AE=EC,于是有
BC= AB比一比:看 谁 算 的 快1.如图:在Rt△ABC中
∠A=300,AB=12cm
则BC=_____cm62.如图:△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8cm,
BD=___, BE=_______4cm 2cm应用新知,巩固提高 例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC 、 DE要多长?解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又AD=1/2AB,
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.1、如图,在Rt△ABC中, ∠B=2 ∠A,AB=6cm,则BC=________.2、如图, Rt△ABC中, ∠A= 30°,AB+BC=12cm,则AB= _______.3cm8cm3、如图, Rt△ABC中, ∠A= 30°,BD
平分∠ABC,且BD=16cm,则AC= .D24cmAD=2CD成立吗?练一练4、如图,在△ABC中, ∠ACB= 90°,BA的
垂直平分线交边CB于D。若AB=10,AC=5,
则图中等于 30°的角的个数为( )A.2 B.3
C.4 D.5B5、如图,在△ABC中, AB=AC,
∠BAC= 120°,AC的垂直平分线EF交AC
于点E,交BC于点F。求证:BF=2CF6、如图,上午9时,一条渔船从A出发,以12海里/时的速度向正北航行,11时到达B处,从A、B两处望小岛C,测得∠NAC=150, ∠NBC=300,若小岛周围12.3海里内有暗礁,问该渔船继续向正北航行有无触礁的危险?NABCD经过本节课的学习,你有哪些收获?共同回顾 如图,在△ABC中, ∠ACB= 90°,
∠B= 15°,AB的垂直平分线分别交BC、AB
于D、E。求证:DB=2ACBEDAC当堂检测,自我评价
