13.3.1 等腰三角形课件
文档属性
| 名称 | 13.3.1 等腰三角形课件 |  | |
| 格式 | zip | ||
| 文件大小 | 858.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-19 22:46:49 | ||
图片预览







文档简介
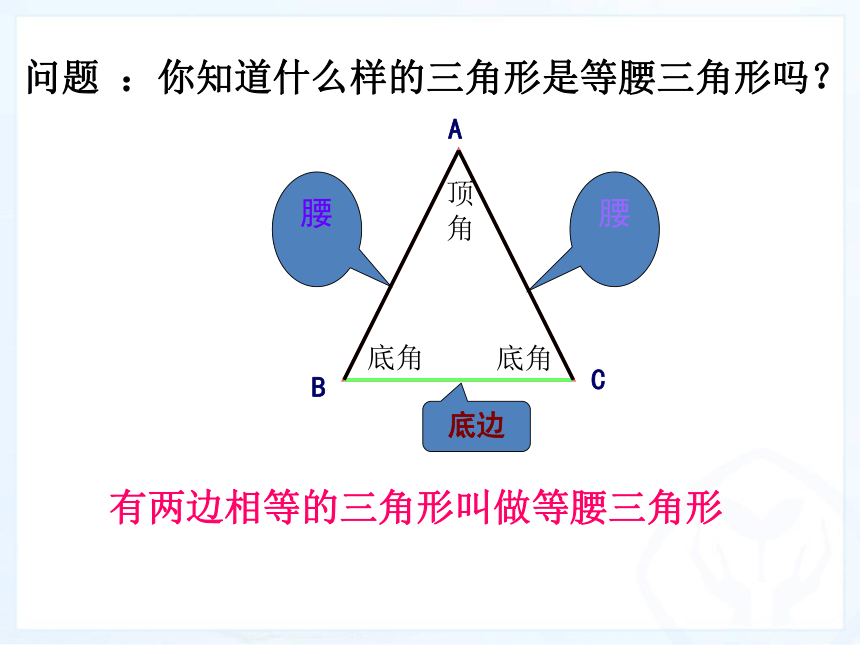
课件23张PPT。问题 :你知道什么样的三角形是等腰三角形吗?
底边底角底角顶角有两边相等的三角形叫做等腰三角形八年级 上册13.3 等腰三角形 (第1课时)学习目标:
1. 知道等腰三角形轴对称图形.
2.探索并证明等腰三角形的两个性质.
3. 学会用代数方法(列方程)解几何问题。
学习重点:
探索并证明等腰三角形性质.
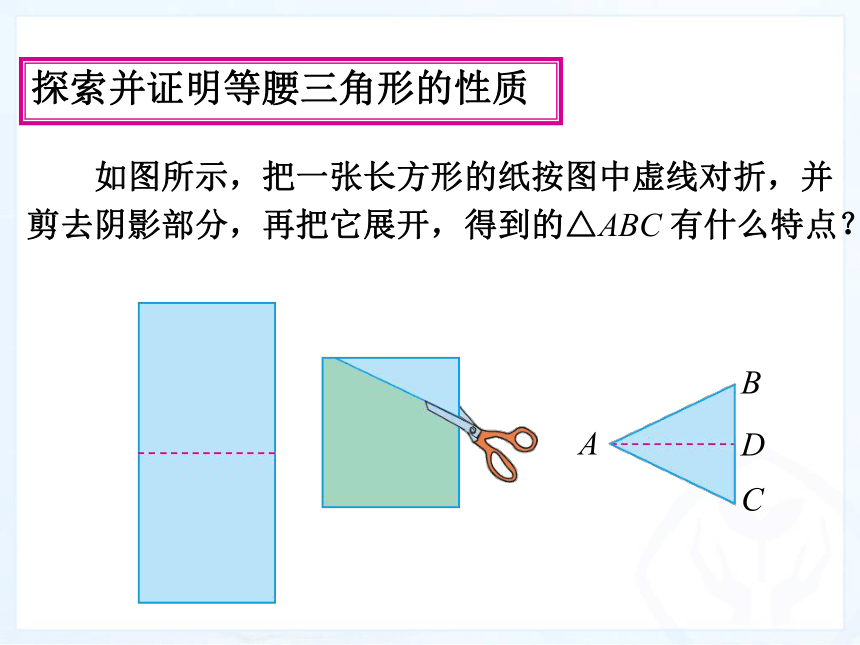
① 等腰三角形的两个底角相等,简称“等边对等角”②等腰三角形的顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一” 如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?探索并证明等腰三角形的性质 探索并证明等腰三角形的性质 仔细观察自己剪出的等腰三角形纸片,你能发现这
个等腰三角形有什么特征吗? 等腰三角形的特征:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.证明等腰三角形的性质 等腰三角形的性质:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合. 已知:如图,△ABC 中,AB =AC.求证:∠B =∠C.证明等腰三角形的性质 1 证明:作底边的中线AD.
∴ BD =CD,
∴ 在△ABD 和△ACD 中
BD =CD
AB =AC
AD =AD
∴ △ABD ≌△ACD(SSS).∴ ∠B =∠C. (1)等腰三角形的两个底角相等;D 你还有其他方法证明性质1吗?
简称“等边对等角” 证明等腰三角形的性质 2(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
D 已知:如图,△ABC 中,AB =AC,AD 是底边BC 的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:由(1)知
△ABD ≌△ACD(SSS). ∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.简称“三线合一”
探索并证明等腰三角形的性质 在等腰三角形性质的探索过程和证明过程中,“折
痕”“辅助线”发挥了非常重要的作用,由此,你能发
现等腰三角形具有什么特征?
等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴. 等腰三角形的性质:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.简称“等边对等角”简称“三线合一”
探索并证明等腰三角形的性质 例 题 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.xx2x2x2x课堂练习 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= ;72°课堂练习 练习1 填空:
(2)如图,△ABC 中, AB =AC, ∠B =36°, 则∠A
= °; 108课堂练习 练习1 填空:
(3)已知等腰三角形的一个内角为70°,则它的另外两
个内角的度数分别是 .55°、 55°或70°、 40°课堂练习 练习2 如图,△ABC 是等腰直角三角形(AB =
AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,
∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的
线段. 如图,△ABC 中,AB=AD=DC, ∠BAD= 26°.求∠B和∠C 的度数.课堂练习 (1)本节课学习了哪些主要内容?
(2)我们是怎么探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法?课堂小结 教科书P81页第6、7题.布置作业
底边底角底角顶角有两边相等的三角形叫做等腰三角形八年级 上册13.3 等腰三角形 (第1课时)学习目标:
1. 知道等腰三角形轴对称图形.
2.探索并证明等腰三角形的两个性质.
3. 学会用代数方法(列方程)解几何问题。
学习重点:
探索并证明等腰三角形性质.
① 等腰三角形的两个底角相等,简称“等边对等角”②等腰三角形的顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一” 如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC 有什么特点?探索并证明等腰三角形的性质 探索并证明等腰三角形的性质 仔细观察自己剪出的等腰三角形纸片,你能发现这
个等腰三角形有什么特征吗? 等腰三角形的特征:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.证明等腰三角形的性质 等腰三角形的性质:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合. 已知:如图,△ABC 中,AB =AC.求证:∠B =∠C.证明等腰三角形的性质 1 证明:作底边的中线AD.
∴ BD =CD,
∴ 在△ABD 和△ACD 中
BD =CD
AB =AC
AD =AD
∴ △ABD ≌△ACD(SSS).∴ ∠B =∠C. (1)等腰三角形的两个底角相等;D 你还有其他方法证明性质1吗?
简称“等边对等角” 证明等腰三角形的性质 2(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
D 已知:如图,△ABC 中,AB =AC,AD 是底边BC 的中线.求证:∠BAD =∠CAD,AD⊥BC. 证明:由(1)知
△ABD ≌△ACD(SSS). ∴ ∠BAD =∠CAD,
∠ADB =∠ADC.
∵ ∠ADB +∠ADC =180°,
∴ ∠ADB =90°.
∴ AD⊥BC.简称“三线合一”
探索并证明等腰三角形的性质 在等腰三角形性质的探索过程和证明过程中,“折
痕”“辅助线”发挥了非常重要的作用,由此,你能发
现等腰三角形具有什么特征?
等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴. 等腰三角形的性质:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.简称“等边对等角”简称“三线合一”
探索并证明等腰三角形的性质 例 题 如图,△ABC 中,AB =AC,点D 在AC 上,
且BD =BC =AD.求△ABC 各角的度数.xx2x2x2x课堂练习 练习1 填空:
(1)如图,△ABC 中, AB =AC, ∠A =36°, 则∠B
= ;72°课堂练习 练习1 填空:
(2)如图,△ABC 中, AB =AC, ∠B =36°, 则∠A
= °; 108课堂练习 练习1 填空:
(3)已知等腰三角形的一个内角为70°,则它的另外两
个内角的度数分别是 .55°、 55°或70°、 40°课堂练习 练习2 如图,△ABC 是等腰直角三角形(AB =
AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,
∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的
线段. 如图,△ABC 中,AB=AD=DC, ∠BAD= 26°.求∠B和∠C 的度数.课堂练习 (1)本节课学习了哪些主要内容?
(2)我们是怎么探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法?课堂小结 教科书P81页第6、7题.布置作业
