第6课时 解方程(二)(课件)四年级下册数学北师大版(共18张PPT)
文档属性
| 名称 | 第6课时 解方程(二)(课件)四年级下册数学北师大版(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-17 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
北师大版 四年级下册
解方程(二)
五、认识方程
授课者:杨老师
2020.4.21
复习:
等式两边都加上(或减去)同一个数,等式仍然成立。
学习目标:
1、进一步了解等式的性质是解方程的依据。
2、会用等式的性质(二)解形如“ax=b(a≠0)”
或“x÷a=b(a≠0)”的简单方程。
3、通过天平操作活动,激发探索欲望,培养
学习兴趣。
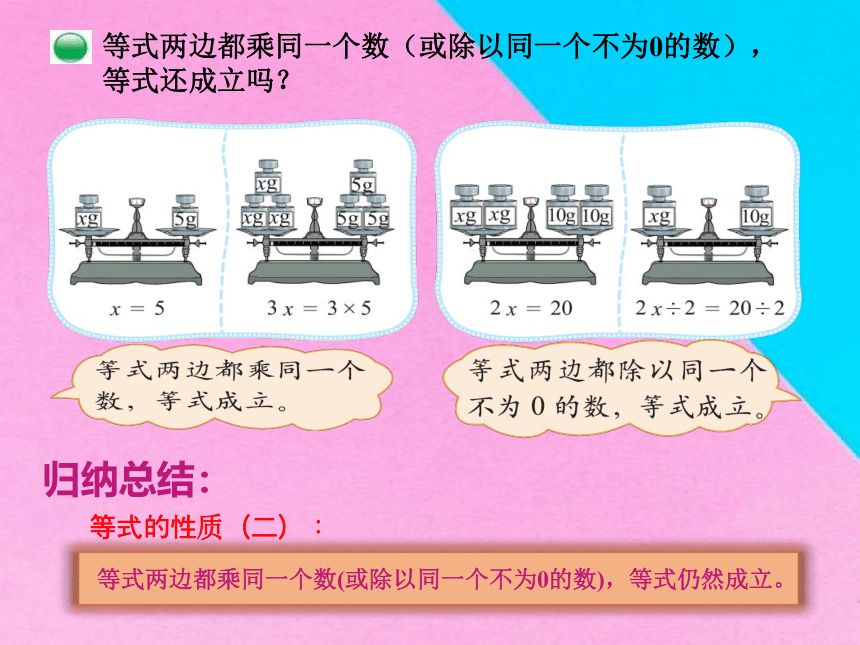
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
5g
g
=5
5g
g
5g
g
=3×5
新课导入
天平平衡,两边砝码的质量相等
结论:
等式两边都乘同一个数,等式仍然成立。
天平仍然平衡,两边砝码的质量相等
左右两边分别加至原来质量的3倍
等式两边都乘同一个数(或除以同一个不为0的数),
等式还成立吗?
10g
10g
=20
g
÷2=20÷2
g
天平平衡,两边砝码的质量相等
结论:
等式两边都除以同一个不为0的数,等式仍然成立。
天平仍然平衡,两边砝码的质量相等
左右两边分别减至原来质量的一半
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
归纳总结:
等式的性质(二):
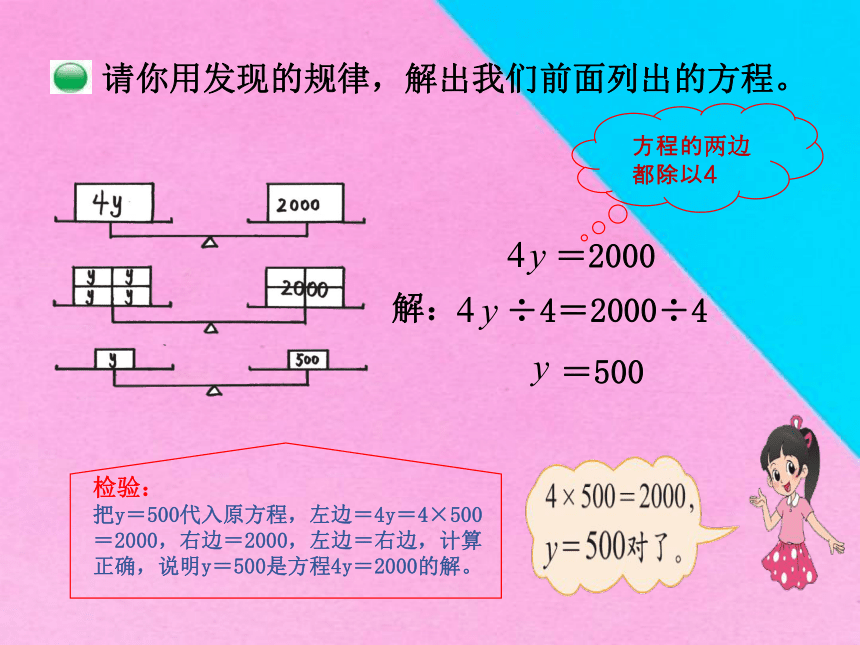
请你用发现的规律,解出我们前面列出的方程。
=2000
解:
÷4=2000÷4
=500
方程的两边都除以4
检验:
把y=500代入原方程,左边=4y=4×500=2000,右边=2000,左边=右边,计算正确,说明y=500是方程4y=2000的解。
解方程。
=28
解:
÷7=28÷7
=4
÷3 =9
解:
÷3×3=9×3
=27
27÷3=9, =27对了。
7×4=28, =4对了。
下面解法正确吗?与同伴交流。
38
1.请你画图或举例说说下面这句话的意思:
等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
如: 20÷5=4
20÷5×2=4×2
8=8
随堂练习
2.森林医生。
=35=35÷7=5
-5=8
解:
-5 =8
=3
-5
-5
+5
+5
=13
=35
解:
÷7=35÷7
=5
3.解方程。
6x÷6=156÷6
3x÷3=630÷3
6x =156
3x = 630
x-47 =47
解:
x =26
解:
x =210
解:
x =94
59+x =120
解:
x =61
x÷52 = 7
x = 364
x÷28 =0
x = 0
解:
解:
x-47+47= 47+47
59+x-59 =120-59
x÷52×52= 7×52
x÷28×28= 0×28
4.长方形游泳池占地600米2,长30米,游泳池宽多
少米?
30x=600
30x÷30=600÷30
x=20
等量关系:长×宽=长方形的面积
解:
答:游泳池宽20米。
5.
⑴这个正方形花坛的边长是多少米?
列方程并解答。
⑵如果把这个花坛改为长方形,周长不变,宽4米,长是多少米?列方程并解答。
等量关系:边长×4=正方形的周长
⑴
解:设这个正方形花坛的边长是x米。
4x = 24
4x÷4=24÷4
x =6
答:这个正方形花坛的边长是6米。
⑵
方法一:
等量关系:长×2+宽×2=长方形的周长
方法二:
等量关系:长+宽=长方形的周长÷2
解:设长是x米。
2x+4×2 = 24
2x+8 = 24
2x+8-8 = 24-8
2x =16
2x÷2 =16÷2
x = 8
解:设长是x米。
x+4 = 24÷2
x+4 = 12
x+4-4= 12-4
x = 8
答:长是8米。
6.某地为便于残疾人轮椅通行,通过了一项关于建筑物前斜坡高度的规定:每1米高的斜坡,至少需要12米的水平长度。
⑴、2米高的斜坡,至少需要多少米的水平长度?
4米、x米高呢?
⑵、某建筑物前的空地长36米,
那么此处斜坡最高多少米?
⑴、
12×2=24(米)
12×4=48(米)
12×x=12 x(米)
答:2米高的斜坡至少需要24米的水平长度,4米高的斜坡至少需要48米的水平长度,x米高的斜坡至少需要12x米的水平长度.
(2)、
解:设此处斜坡最高 x米。
12 x = 36
12 x÷12 = 36÷12
x = 3
答:此处斜坡最高 3米。
课堂小结
通过这节课的学习活动,你有什么收获?谈谈你的感受。
1、通过这节课的学习,我们发现等式两边都乘同一个数
(或除以同一个不为0的数),等式仍然成立。
2、利用等式的性质,我们学会了解简单的方程。
课后作业
1、完成同步导学32页;
2、预习课本72页并完成73页
第2、3题。
同学们再见!
北师大版 四年级下册
解方程(二)
五、认识方程
授课者:杨老师
2020.4.21
复习:
等式两边都加上(或减去)同一个数,等式仍然成立。
学习目标:
1、进一步了解等式的性质是解方程的依据。
2、会用等式的性质(二)解形如“ax=b(a≠0)”
或“x÷a=b(a≠0)”的简单方程。
3、通过天平操作活动,激发探索欲望,培养
学习兴趣。
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
5g
g
=5
5g
g
5g
g
=3×5
新课导入
天平平衡,两边砝码的质量相等
结论:
等式两边都乘同一个数,等式仍然成立。
天平仍然平衡,两边砝码的质量相等
左右两边分别加至原来质量的3倍
等式两边都乘同一个数(或除以同一个不为0的数),
等式还成立吗?
10g
10g
=20
g
÷2=20÷2
g
天平平衡,两边砝码的质量相等
结论:
等式两边都除以同一个不为0的数,等式仍然成立。
天平仍然平衡,两边砝码的质量相等
左右两边分别减至原来质量的一半
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
归纳总结:
等式的性质(二):
请你用发现的规律,解出我们前面列出的方程。
=2000
解:
÷4=2000÷4
=500
方程的两边都除以4
检验:
把y=500代入原方程,左边=4y=4×500=2000,右边=2000,左边=右边,计算正确,说明y=500是方程4y=2000的解。
解方程。
=28
解:
÷7=28÷7
=4
÷3 =9
解:
÷3×3=9×3
=27
27÷3=9, =27对了。
7×4=28, =4对了。
下面解法正确吗?与同伴交流。
38
1.请你画图或举例说说下面这句话的意思:
等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
如: 20÷5=4
20÷5×2=4×2
8=8
随堂练习
2.森林医生。
=35=35÷7=5
-5=8
解:
-5 =8
=3
-5
-5
+5
+5
=13
=35
解:
÷7=35÷7
=5
3.解方程。
6x÷6=156÷6
3x÷3=630÷3
6x =156
3x = 630
x-47 =47
解:
x =26
解:
x =210
解:
x =94
59+x =120
解:
x =61
x÷52 = 7
x = 364
x÷28 =0
x = 0
解:
解:
x-47+47= 47+47
59+x-59 =120-59
x÷52×52= 7×52
x÷28×28= 0×28
4.长方形游泳池占地600米2,长30米,游泳池宽多
少米?
30x=600
30x÷30=600÷30
x=20
等量关系:长×宽=长方形的面积
解:
答:游泳池宽20米。
5.
⑴这个正方形花坛的边长是多少米?
列方程并解答。
⑵如果把这个花坛改为长方形,周长不变,宽4米,长是多少米?列方程并解答。
等量关系:边长×4=正方形的周长
⑴
解:设这个正方形花坛的边长是x米。
4x = 24
4x÷4=24÷4
x =6
答:这个正方形花坛的边长是6米。
⑵
方法一:
等量关系:长×2+宽×2=长方形的周长
方法二:
等量关系:长+宽=长方形的周长÷2
解:设长是x米。
2x+4×2 = 24
2x+8 = 24
2x+8-8 = 24-8
2x =16
2x÷2 =16÷2
x = 8
解:设长是x米。
x+4 = 24÷2
x+4 = 12
x+4-4= 12-4
x = 8
答:长是8米。
6.某地为便于残疾人轮椅通行,通过了一项关于建筑物前斜坡高度的规定:每1米高的斜坡,至少需要12米的水平长度。
⑴、2米高的斜坡,至少需要多少米的水平长度?
4米、x米高呢?
⑵、某建筑物前的空地长36米,
那么此处斜坡最高多少米?
⑴、
12×2=24(米)
12×4=48(米)
12×x=12 x(米)
答:2米高的斜坡至少需要24米的水平长度,4米高的斜坡至少需要48米的水平长度,x米高的斜坡至少需要12x米的水平长度.
(2)、
解:设此处斜坡最高 x米。
12 x = 36
12 x÷12 = 36÷12
x = 3
答:此处斜坡最高 3米。
课堂小结
通过这节课的学习活动,你有什么收获?谈谈你的感受。
1、通过这节课的学习,我们发现等式两边都乘同一个数
(或除以同一个不为0的数),等式仍然成立。
2、利用等式的性质,我们学会了解简单的方程。
课后作业
1、完成同步导学32页;
2、预习课本72页并完成73页
第2、3题。
同学们再见!
