【新教材】人教版数学六年级上册3-8 解决问题(例7)教学课件(共25张PPT)
文档属性
| 名称 | 【新教材】人教版数学六年级上册3-8 解决问题(例7)教学课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 13:37:48 | ||
图片预览








文档简介
(共25张PPT)
8. 解决问题(三)
新课标人教版六年级数学上册
第三单元 分数除法
在探索解决问题方法的过程中,学会利用单位“1”解决与分数除法有关的实际问题。
1
核心素养
在探索问题时,经历猜想、尝试和获得结论的过程,积累解决问题的经验,体会并掌握数学模型思想。
2
在解决问题的过程中,体会数学与生活的密切联系,感受学习分数除法的价值,培养学习数学的兴趣,树立学好数学的信心。
3
01
情景导学
情景导学
中国公路 总里程已达532万公里、高速公路达14.26万公里,居世界第一。早在新中国成立之初,全国能通车的公路仅8.08万公里。我国农村公路总里程已超过404万公里,预计具备条件的乡镇和建制村100%通硬化路目标将如期实现。2022年,西藏公路通车里程突破12万公里,一级以上公路通车里程达1105公里。
情景导学
1.修路队修一条公路,每天修25m,20天修完,这条公路长多少米
25×20=500(m)
工作效率×工作时间=工作总量
2.修路队修一条500m的公路,20天修完,平均每天修多少米
500÷20=25(m)
工作总量÷工作时间=工作效率
3.修路队修一条500m的公路,每天修25 m,多少天能修完
500÷25=20(m)
工作总量÷工作效率=工作时间
探索发现
02
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
阅读与理解
知道了两个队单独修完需要的时间,要求的是_______________________
两队合修,需要的时间。
这条路有多长呢?
探索发现
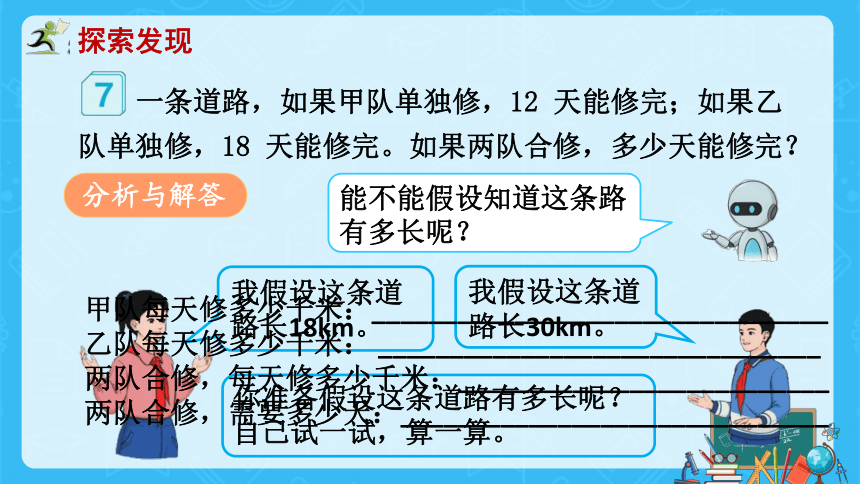
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长18km。
我假设这条道路长30km。
你准备假设这条道路有多长呢?自己试一试,算一算。
甲队每天修多少千米:________________________________
乙队每天修多少千米: _______________________________
两队合修,每天修多少千米:__________________________
两队合修,需要多少天:______________________________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有 18 km。
根据假设的这条路的长度,请你列式计算。
甲队每天修多少千米:________________
乙队每天修多少千米: ________________
两队合修,每天修多少千米:___________
两队合修,需要多少天:_______________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有30km。
根据假设的这条路的长度,请你列式计算。
甲队每天修多少千米:________________
乙队每天修多少千米: ________________
两队合修,每天修多少千米:___________
两队合修,需要多少天:_______________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路是1。
根据假设的这条路的长度,请你列式计算。
甲队每天修多少千米:________________
乙队每天修多少千米: ________________
两队合修,每天修多少千米:___________
两队合修,需要多少天:_______________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
假设这条道路有18km。
假设这条道路有30km。
假设这条道路是1。
不同的方法计算出的结果一样吗?
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
回顾与反思
答:如果两队合修, 天可以修完。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成“1”,很简便。
怎样才知道以上的解决方法是否正确? 把你的想法写下来,和同学交流一下。
探索发现
归纳:解决工程问题要注意:
(1)把工作总量看做单位“1”。
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率。
(3)基本关系式:工作总量÷工作效率之和=工作时间。
学以致用
03
学以致用
1.一批货物,只用甲车运,6 次能运完;只用乙车运,3 次运完。如果两辆车一起运,多少次能运完这批货物?
答:两辆车一起运,2次能运完这批货物。
把这批货物看作“1”
学以致用
2.(P42 6)挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?
答:两人合作,12天能挖完。
“1”
学以致用
3.(P42 7)甲车从 A 城市到 B 城市要行驶 2 小时,乙车从 B 城市到 A 城市要行驶 3 小时。两车同时分别从 A 城市和 B 城市出发,几小时后相遇?
答: 小时后相遇。
学以致用
4.(P42 8)某水库准备打开泄洪口调节水位。只打开 A 口,8小时可以完成任务;只打开B口,6小时可以完成任务。如果两个泄洪口同时打开,几小时可以完成任务?
答: 小时可以完成任务。
学以致用
5.(P42 8)植树队要种 300 棵树。甲队单独种,种完需要
8天;乙队单独种,种完需要10天。现在两队合种,5 天能种完吗?
答:现在两队合种,5天能种完。
易错点:当工作总量用具体量计算时,要注意工作效率也要用具体量表示。如:用300计算时,一队的工作效率是 300÷8。
课堂总结
04
课堂总结
这节课你们都学会了哪些知识?
将工作总量看作单位“1”,用单位时间内完成工作总量的几分之一表示工作效率。
基本等量关系式:工作总量÷工作效率之和=工作时间
布置作业
分层作业对应习题
8. 解决问题(三)
新课标人教版六年级数学上册
第三单元 分数除法
在探索解决问题方法的过程中,学会利用单位“1”解决与分数除法有关的实际问题。
1
核心素养
在探索问题时,经历猜想、尝试和获得结论的过程,积累解决问题的经验,体会并掌握数学模型思想。
2
在解决问题的过程中,体会数学与生活的密切联系,感受学习分数除法的价值,培养学习数学的兴趣,树立学好数学的信心。
3
01
情景导学
情景导学
中国公路 总里程已达532万公里、高速公路达14.26万公里,居世界第一。早在新中国成立之初,全国能通车的公路仅8.08万公里。我国农村公路总里程已超过404万公里,预计具备条件的乡镇和建制村100%通硬化路目标将如期实现。2022年,西藏公路通车里程突破12万公里,一级以上公路通车里程达1105公里。
情景导学
1.修路队修一条公路,每天修25m,20天修完,这条公路长多少米
25×20=500(m)
工作效率×工作时间=工作总量
2.修路队修一条500m的公路,20天修完,平均每天修多少米
500÷20=25(m)
工作总量÷工作时间=工作效率
3.修路队修一条500m的公路,每天修25 m,多少天能修完
500÷25=20(m)
工作总量÷工作效率=工作时间
探索发现
02
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
阅读与理解
知道了两个队单独修完需要的时间,要求的是_______________________
两队合修,需要的时间。
这条路有多长呢?
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
能不能假设知道这条路有多长呢?
我假设这条道路长18km。
我假设这条道路长30km。
你准备假设这条道路有多长呢?自己试一试,算一算。
甲队每天修多少千米:________________________________
乙队每天修多少千米: _______________________________
两队合修,每天修多少千米:__________________________
两队合修,需要多少天:______________________________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有 18 km。
根据假设的这条路的长度,请你列式计算。
甲队每天修多少千米:________________
乙队每天修多少千米: ________________
两队合修,每天修多少千米:___________
两队合修,需要多少天:_______________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有30km。
根据假设的这条路的长度,请你列式计算。
甲队每天修多少千米:________________
乙队每天修多少千米: ________________
两队合修,每天修多少千米:___________
两队合修,需要多少天:_______________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路是1。
根据假设的这条路的长度,请你列式计算。
甲队每天修多少千米:________________
乙队每天修多少千米: ________________
两队合修,每天修多少千米:___________
两队合修,需要多少天:_______________
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
假设这条道路有18km。
假设这条道路有30km。
假设这条道路是1。
不同的方法计算出的结果一样吗?
探索发现
一条道路,如果甲队单独修,12 天能修完;如果乙队单独修,18 天能修完。如果两队合修,多少天能修完?
回顾与反思
答:如果两队合修, 天可以修完。
不管假设这条道路有多长,答案都是相同的。把道路长度假设成“1”,很简便。
怎样才知道以上的解决方法是否正确? 把你的想法写下来,和同学交流一下。
探索发现
归纳:解决工程问题要注意:
(1)把工作总量看做单位“1”。
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率。
(3)基本关系式:工作总量÷工作效率之和=工作时间。
学以致用
03
学以致用
1.一批货物,只用甲车运,6 次能运完;只用乙车运,3 次运完。如果两辆车一起运,多少次能运完这批货物?
答:两辆车一起运,2次能运完这批货物。
把这批货物看作“1”
学以致用
2.(P42 6)挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?
答:两人合作,12天能挖完。
“1”
学以致用
3.(P42 7)甲车从 A 城市到 B 城市要行驶 2 小时,乙车从 B 城市到 A 城市要行驶 3 小时。两车同时分别从 A 城市和 B 城市出发,几小时后相遇?
答: 小时后相遇。
学以致用
4.(P42 8)某水库准备打开泄洪口调节水位。只打开 A 口,8小时可以完成任务;只打开B口,6小时可以完成任务。如果两个泄洪口同时打开,几小时可以完成任务?
答: 小时可以完成任务。
学以致用
5.(P42 8)植树队要种 300 棵树。甲队单独种,种完需要
8天;乙队单独种,种完需要10天。现在两队合种,5 天能种完吗?
答:现在两队合种,5天能种完。
易错点:当工作总量用具体量计算时,要注意工作效率也要用具体量表示。如:用300计算时,一队的工作效率是 300÷8。
课堂总结
04
课堂总结
这节课你们都学会了哪些知识?
将工作总量看作单位“1”,用单位时间内完成工作总量的几分之一表示工作效率。
基本等量关系式:工作总量÷工作效率之和=工作时间
布置作业
分层作业对应习题
