【新教材】人教版数学六年级上册8-1 数与形(例1)教学课件(共23张PPT)
文档属性
| 名称 | 【新教材】人教版数学六年级上册8-1 数与形(例1)教学课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 13:51:56 | ||
图片预览





文档简介
(共23张PPT)
1.数与形(例1)
新课标人教版六年级数学上册
第八单元 数学广角
体会数与形的联系,进一步积累数形结合的数学活动经验,培养学生数形结合的数学思想意识。
1
核心素养
体验数形结合的数学思想方法价值,激发学生用数形结合的思想方法解决问题的兴趣,感受数学的魅力。
2
在解决数学问题的过程中,体会和掌握数形结合、归纳推理等基本的数学思想方法。
3
01
情景导学
情景导学
先计算出结果,再说一说你发现了什么?
1+3=( )
4
1+3+5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+…+21=( )
100
连续的奇数相加
探索发现
02
探索发现
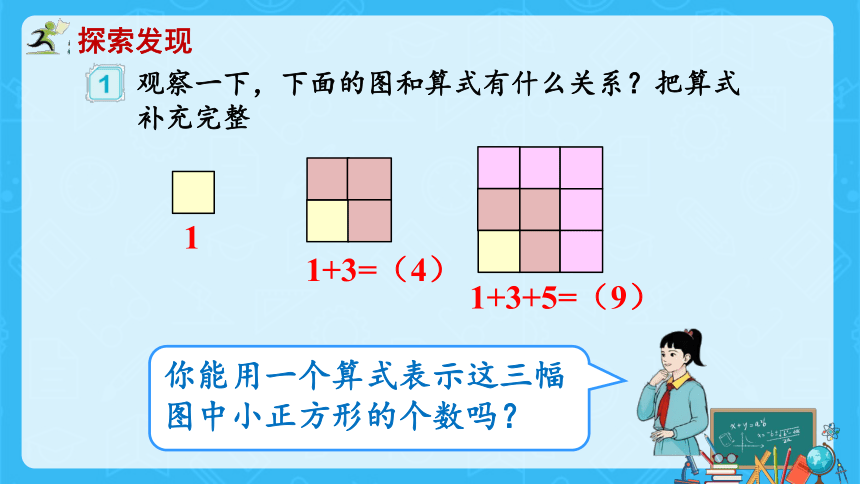
你能用一个算式表示这三幅图中小正方形的个数吗?
1
1+3=(4)
1+3+5=(9)
观察一下,下面的图和算式有什么关系?把算式补充完整
探索发现
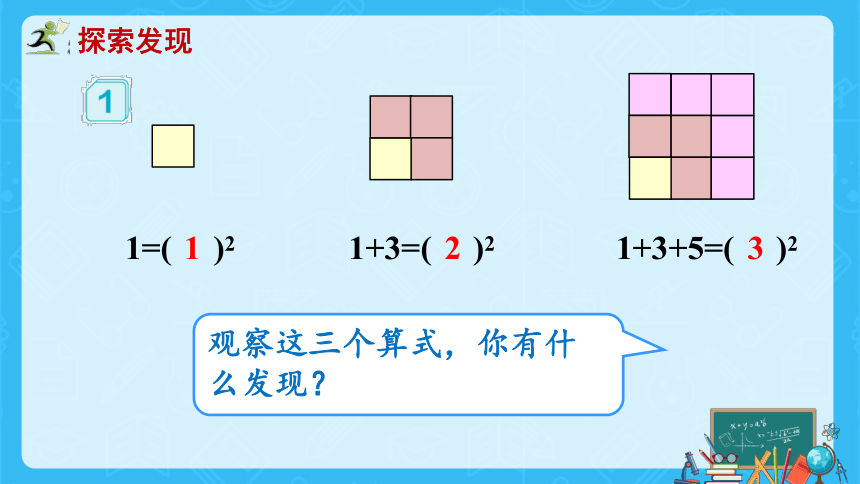
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
观察这三个算式,你有什么发现?
探索发现
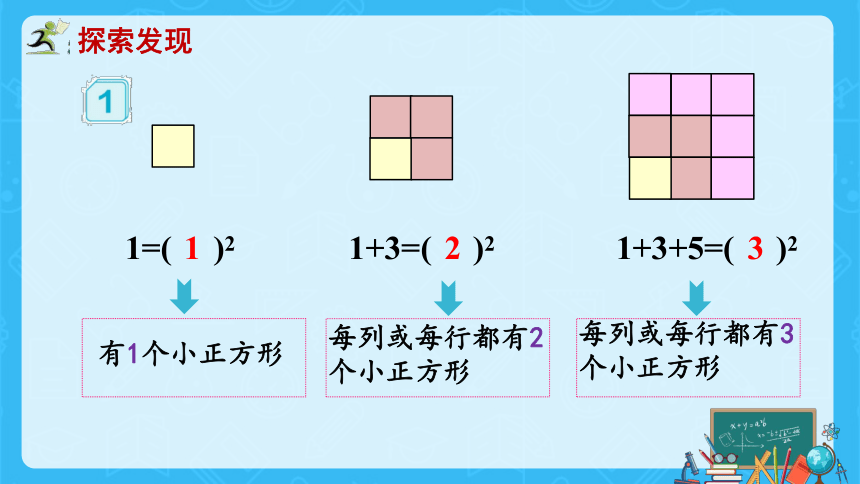
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
探索发现
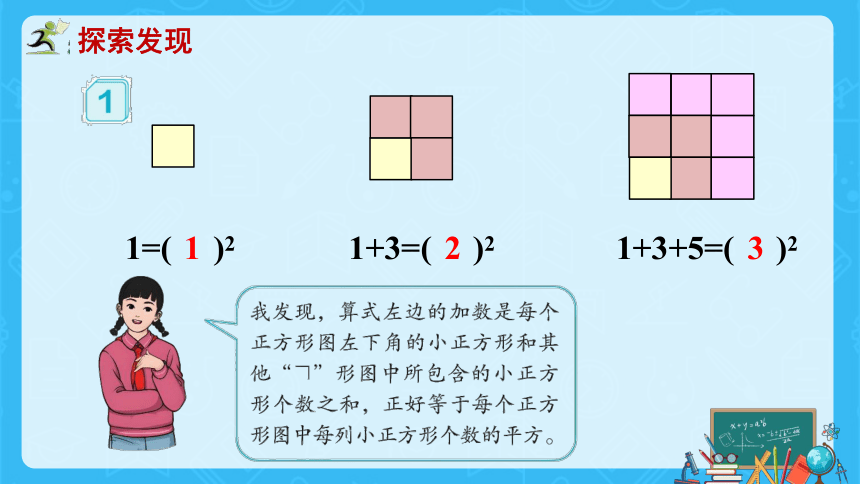
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
探索发现
从1开始的连续奇数的和正好是这串数个数的平方。
每一个图形的个数正好等于从左下角加上其它“┐” 形图中所包含的个数。
图形
数形结合
算式
图形和算式有什么关系?
说一说你的发现,并用自己的语言解释规律。
探索发现
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
探索发现
利用规律直接写一写。
如果遇到困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13 =( )2
1+3+5+7+9+11+13+15+17
4
7
______________________________=( 9 )2
易错点:只有从1开始的连续奇数相加的和才是平方数。
学以致用
03
学以致用
1. 请你根据例1的结论算一算。
3个奇数
1+3+5+7+5+3+1 =( )
25
85
4个奇数
42
32
+
7个奇数
6个奇数
72
62
+
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
学以致用
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
绿色:
蓝色:
1
8
2
10
3
12
4
14
学以致用
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形
绿色:
蓝色:
1
8
2
10
3
12
4
14
第6个图形:6个绿色18个蓝色。
第10个图形:10个绿色26个蓝色。
道理:任意两张相邻的图中,绿色相差1个,蓝色相差2个。
学以致用
3. (1/P107)下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:3行3列
内圈个数:1行1列
学以致用
3. (1/P107)下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:5行5列
内圈个数:3行3列
=16
学以致用
3. (1/P107)下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有40个小正方形。
32-12
=8
52- 32
=16
72- 52
=24
92- 72
=32
112- 92
=40
总个数:11行11列
内圈个数:9行9列
总个数:9行9列
内圈个数:7行7列
课堂总结
04
课堂总结
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
布置作业
分层作业对应习题
1.数与形(例1)
新课标人教版六年级数学上册
第八单元 数学广角
体会数与形的联系,进一步积累数形结合的数学活动经验,培养学生数形结合的数学思想意识。
1
核心素养
体验数形结合的数学思想方法价值,激发学生用数形结合的思想方法解决问题的兴趣,感受数学的魅力。
2
在解决数学问题的过程中,体会和掌握数形结合、归纳推理等基本的数学思想方法。
3
01
情景导学
情景导学
先计算出结果,再说一说你发现了什么?
1+3=( )
4
1+3+5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+…+21=( )
100
连续的奇数相加
探索发现
02
探索发现
你能用一个算式表示这三幅图中小正方形的个数吗?
1
1+3=(4)
1+3+5=(9)
观察一下,下面的图和算式有什么关系?把算式补充完整
探索发现
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
观察这三个算式,你有什么发现?
探索发现
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
探索发现
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
探索发现
从1开始的连续奇数的和正好是这串数个数的平方。
每一个图形的个数正好等于从左下角加上其它“┐” 形图中所包含的个数。
图形
数形结合
算式
图形和算式有什么关系?
说一说你的发现,并用自己的语言解释规律。
探索发现
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
探索发现
利用规律直接写一写。
如果遇到困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13 =( )2
1+3+5+7+9+11+13+15+17
4
7
______________________________=( 9 )2
易错点:只有从1开始的连续奇数相加的和才是平方数。
学以致用
03
学以致用
1. 请你根据例1的结论算一算。
3个奇数
1+3+5+7+5+3+1 =( )
25
85
4个奇数
42
32
+
7个奇数
6个奇数
72
62
+
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
学以致用
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
绿色:
蓝色:
1
8
2
10
3
12
4
14
学以致用
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形
绿色:
蓝色:
1
8
2
10
3
12
4
14
第6个图形:6个绿色18个蓝色。
第10个图形:10个绿色26个蓝色。
道理:任意两张相邻的图中,绿色相差1个,蓝色相差2个。
学以致用
3. (1/P107)下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:3行3列
内圈个数:1行1列
学以致用
3. (1/P107)下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:5行5列
内圈个数:3行3列
=16
学以致用
3. (1/P107)下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有40个小正方形。
32-12
=8
52- 32
=16
72- 52
=24
92- 72
=32
112- 92
=40
总个数:11行11列
内圈个数:9行9列
总个数:9行9列
内圈个数:7行7列
课堂总结
04
课堂总结
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
布置作业
分层作业对应习题
