华东师大版八年级数学上册12.3乘法公式同步练习题(含解析)
文档属性
| 名称 | 华东师大版八年级数学上册12.3乘法公式同步练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 90.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 13:21:36 | ||
图片预览



文档简介
2022-2023学年华东师大版八年级数学上册《12.3乘法公式》同步练习题(附答案)
一.选择题
1.计算(a﹣2b)2=( )
A.a2﹣4ab+4b2 B.a2+4ab+4b2 C.a2﹣4ab﹣4b2 D.a2+4ab﹣4b2
2.在下列各项中,可以用平方差公式计算的是( )
A.(2a+3b)(3a﹣2b) B.(a+b)(﹣a﹣b)
C.(﹣m+n)(m﹣n) D.(a+b)(b﹣a)
3.下列运算中正确的是( )
A.(x+2)(x﹣2)=x2﹣2 B.(﹣3a﹣2)(3a﹣2)=4﹣9a2
C.(a+b)2=a2+b2 D.(a﹣b)2=a2﹣ab+b2
4.若(a+b)2=10,a2+b2=4,则ab的值为( )
A.14 B.7 C.6 D.3
5.图(1)是一个长为a,宽为b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是( )
A.a2 B.b2 C.(a﹣b)2 D.(a﹣b)2
6.如果x2﹣kxy+9y2是一个完全平方式,那么k的值是( )
A.3 B.±6 C.6 D.±3
7.计算(15x2y﹣10xy2)÷5xy的结果为( )
A.3x﹣2xy B.3xy﹣2y C.3x﹣2y D.3x2﹣2y2
8.如图甲,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形如图乙,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2
D.a2﹣b2=(a+b)(a﹣b)
二.填空题
9.计算:(x4﹣4x3)÷x2= .
10.已知(x+y)2=18,xy=5,则x2+y2的值为 .
11.若多项式4x2﹣kx+25是一个完全平方式,则k的值是 .
12.若a﹣b=8,ab=2,则a2+b2的值为 .
13.已知(a+b)2=7,(a﹣b)2=3,则ab= .
14.小明在计算一个二项式的平方时,得到的正确结果是4x2+12xy+■,但最后一项不慎被污染了,这一项应是 .
15.数学课上老师让同学们用若干个小矩形,拼成一个大矩形,如图所示,请你仔细观察图形,写出图中所表示的整式的乘法关系式为 .
16.已知a>0,b>0,(3a+3b+1)(3a+3b﹣1)=899,则a+b= .
17.当一个正方形的边长增加5cm时,它的面积增加85cm2,则原来正方形的边长是 cm.
18.小丽在计算3×(4+1)×(42+1)时,把3写成(4﹣1)后,发现可以连续运用平方差公式进行计算.用类似方法计算:(1+)×(1+)×(1+)×(1+)+= .
三.解答题
19.计算:(x﹣2y)(x+2y)﹣(x+2y)2.
20.计算:
(1)(3x+1)(x﹣2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
21.已知(x+y)2=25,(x﹣y)2=1,求x2+y2与xy的值.
22.先化简,再求值:(2m+1)(2m﹣1)﹣(m﹣1)2+(2m)3÷(﹣8m),其中m2+m﹣2=0.
23.先化简,再求值:(a﹣b)2﹣2a(a+3b)+(a+2b)(a﹣2b),其中a=1,b=﹣3.
24.已知多项式A=x2+2x+n2,多项式B=2x2+4x+3n2+3.
(1)若多项式x2+2x+n2是完全平方式,则n= ;
(2)已知x=m时,多项式x2+2x+n2的值为﹣1,则x=﹣m时,该多项式的值为多少?
(3)判断多项式A与B的大小关系并说明理由.
25.图1,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中的阴影部分的面积为 ;
(2)观察图2,三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 ;
(3)若x+y=﹣6,xy=2.75,求x﹣y;
(4)观察图3,你能得到怎样的代数恒等式呢?
26.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2+ab=a(a+b)
(2)应用:利用你从(1)选出的等式,完成下列各题:
①已知9x2﹣4y2=24,3x+2y=6,求3x﹣2y的值;
②计算:.
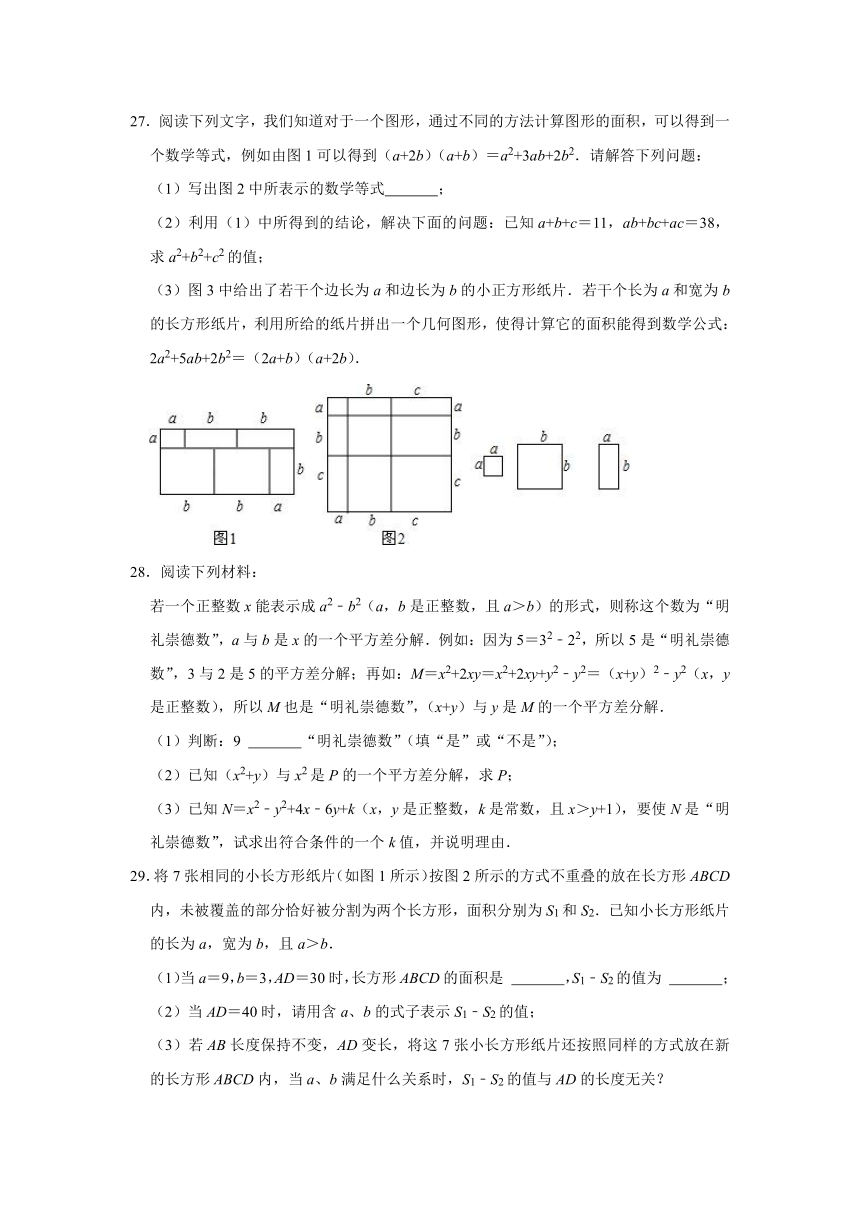
27.阅读下列文字,我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片.若干个长为a和宽为b的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:2a2+5ab+2b2=(2a+b)(a+2b).
28.阅读下列材料:
若一个正整数x能表示成a2﹣b2(a,b是正整数,且a>b)的形式,则称这个数为“明礼崇德数”,a与b是x的一个平方差分解.例如:因为5=32﹣22,所以5是“明礼崇德数”,3与2是5的平方差分解;再如:M=x2+2xy=x2+2xy+y2﹣y2=(x+y)2﹣y2(x,y是正整数),所以M也是“明礼崇德数”,(x+y)与y是M的一个平方差分解.
(1)判断:9 “明礼崇德数”(填“是”或“不是”);
(2)已知(x2+y)与x2是P的一个平方差分解,求P;
(3)已知N=x2﹣y2+4x﹣6y+k(x,y是正整数,k是常数,且x>y+1),要使N是“明礼崇德数”,试求出符合条件的一个k值,并说明理由.
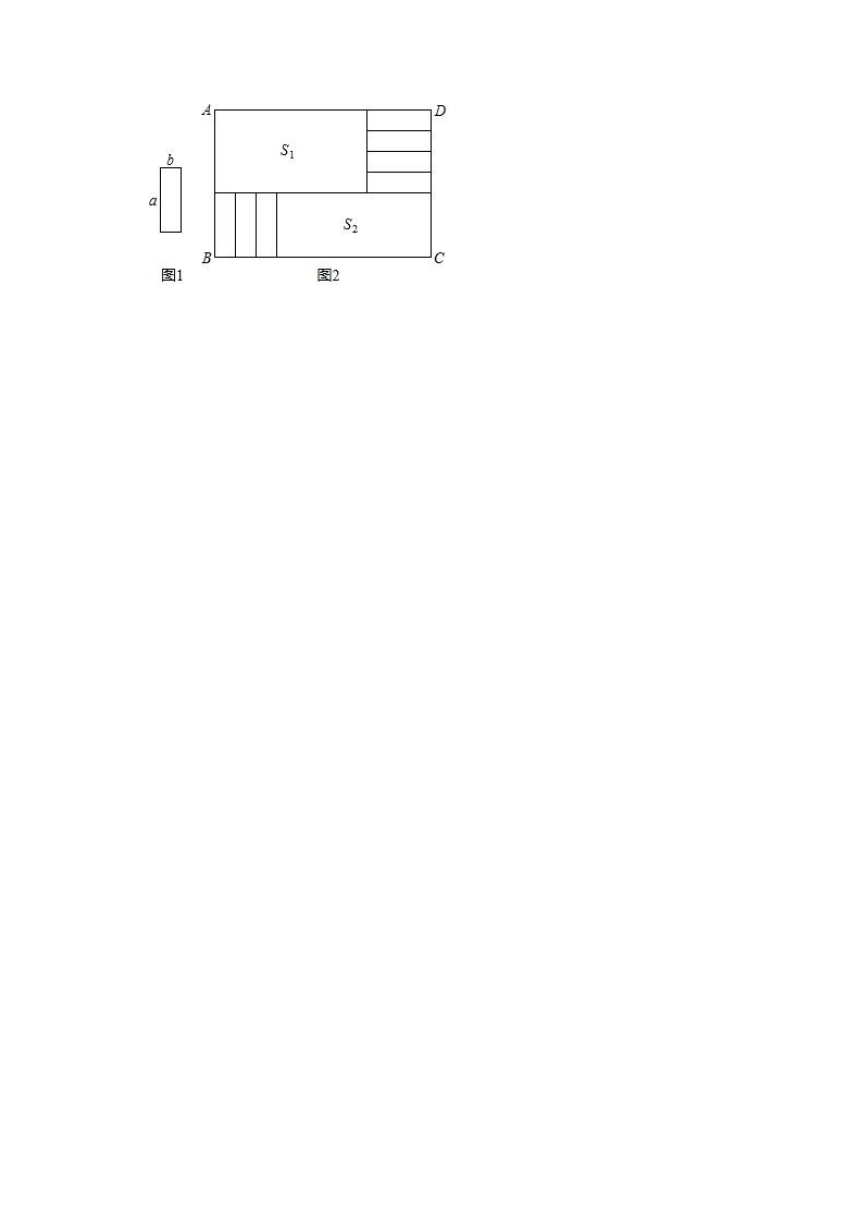
29.将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S1﹣S2的值为 ;
(2)当AD=40时,请用含a、b的式子表示S1﹣S2的值;
(3)若AB长度保持不变,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,当a、b满足什么关系时,S1﹣S2的值与AD的长度无关?
参考答案
一.选择题
1.解:原式=a2﹣2a 2b+(2b)2
=a2﹣4ab+4b2,
故选:A.
2.解:A、(2a+3b)(3a﹣2b),不符合平方差公式的结构特征,故错误;
B、(a+b)(﹣a﹣b),不符合平方差公式的结构特征,故错误;
C、(﹣m+n)(m﹣n),不符合平方差公式的结构特征,故错误;
D、,符合平方差公式的结构特征,故正确;
故选:D.
3.解:A、(x+2)(x﹣2)=x2﹣4,错误;
B、(﹣3a﹣2)(3a﹣2)=4﹣9a2,正确;
C、(a+b)2=a2+2ab+b2,错误;
D、(a﹣b)2=a2﹣2ab+b2,错误;
故选:B.
4.解:∵(a+b)2=10,a2+b2=4,(a+b)2=a2+2ab+b2,
∴ab=[(a+b)2﹣(a2+b2)]=×(10﹣4)=3.
故选:D.
5.解:由题意得所剪得的每个小长方形的长为,宽为,
∴中间空余的部分的是一个边长为﹣的正方形,
∴中间空余的部分的面积是()2.
故选:D.
6.解:∵x2﹣kxy+9y2是一个完全平方式,
∴k=±6.
故选:B.
7.解:原式=15x2y÷5xy﹣10xy2÷5xy
=3x﹣2y,
故选:C.
8.解:图甲的面积=大正方形的面积﹣空白处正方形的面积=a2﹣b2;
图乙中矩形的长=a+b,宽=a﹣b,图乙的面积=(a+b)(a﹣b).
所以a2﹣b2=(a+b)(a﹣b).
故选:D.
二.填空题
9.解:原式=x4÷x2﹣4x3÷x2
=x2﹣4x,
故答案为:x2﹣4x.
10.解:∵(x+y)2=18,xy=5,
∴x2+y2+2xy=x2+y2+10=18.
∴x2+y2=8.
故答案为:8.
11.解:∵4x2﹣kx+25是一个完全平方式,
∴4x2﹣kx+25=(2x)2﹣kx+52=(2x±5)2,
∵(2x±5)2=4x2±20x+25,
∴﹣kx=±20x,解得k=±20.
故答案为:±20.
12.解:∵a﹣b=8,ab=2,
∴a2+b2=(a﹣b)2+2ab=64+4=68.
故答案为:68.
13.解:(a+b)2﹣(a﹣b)2=4ab=7﹣3=4,
所以可得:ab=1,
故答案为:1
14.解:∵4x2+12xy+■是一个二项式的平方,
∴■=(3y)2=9y2.
故答案为:9y2.
15.解:由拼图可得,大长方形的长为a+2b,宽为a+b,
所以面积为(a+2b)(a+b),
根据各个部分面积和为a2+3ab+2b2,
因此有(a+2b)(a+b)=a2+3ab+2b2,
故答案为:(a+2b)(a+b)=a2+3ab+2b2.
16.解:∵(3a+3b+1)(3a+3b﹣1)=899,
∴(3a+3b)2﹣1=899,
即(3a+3b)2=900,
又∵(±30)2=900,a>0,b>0,
∴3a+3b=30,
即a+b=10,
故答案为:10.
17.解:设原正方形边长为xcm,则增加后边长为(x+5)cm,
根据题意列方程得:(x+5)2﹣x2=85,
整理得10x+25=85,
解得x=6,
∴原来正方形边长为6cm.
故答案为:6.
18.解:(1+)×(1+)×(1+)×(1+)+
=
=×
=
=
=
=
=2.
故答案为:2.
三.解答题
19.解:(x﹣2y)(x+2y)﹣(x+2y)2
=(x2﹣4y2)﹣(x2+4y2+4xy)
=x2﹣4y2﹣x2﹣4y2﹣4xy
=﹣8y2﹣4xy.
20.解:(1)原式=3x2﹣6x+x﹣2
=3x2﹣5x﹣2;
(2)原式=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
21.解:∵(x+y)2=x2+2xy+y2=25①,(x﹣y)2=x2﹣2xy+y2=1②,
∴①+②得:2(x2+y2)=26,即x2+y2=13;
①﹣②得:4xy=24,即xy=6.
22.解:原式=4m2﹣1﹣(m2﹣2m+1)+8m3÷(﹣8m)
=4m2﹣1﹣m2+2m﹣1﹣m2
=2m2+2m﹣2
=2(m2+m)﹣2,
∵m2+m﹣2=0,
∴m2+m=2,
当m2+m=2时,原式=2×2﹣2=2.
23.解:原式=a2﹣2ab+b2﹣2a2﹣6ab+a2﹣4b2=﹣8ab﹣3b2.
当a=1、b=﹣3时,
原式=﹣8×1×(﹣3)﹣3×(﹣3)2
=24﹣27
=﹣3.
24.解:(1)∵x2+2x+n2是一个完全平方式,
∴n2=1,
∴n=±1.
故答案为:1或﹣1;
(2)当x=m时m2+2m+n2=﹣1,
∴m2+2m+1+n2=0,
∴(m+1)2+n2=0,
∵(m+1)2≥0,n2≥0,
∴x=m=﹣1,n=0,
∴x=﹣m时,多项式x2+2x+n2的值为m2﹣2m+n2=3;
(3)B>A.
理由如下:B﹣A=2x2+4x+3n2+3﹣(x2+2x+n2)=x2+2x+2n2+3=(x+1)2+2n2+2,
∵(x+1)2≥0,2n2≥0,
∴(x+1)2+2n2+2>0,
∴B>A.
25.解:(1)图②中的阴影部分的面积为(m﹣n)2,
故答案为:(m﹣n)2;
(2)(m+n)2﹣4mn=(m﹣n)2,
故答案为:(m+n)2﹣4mn=(m﹣n)2;
(3)(x﹣y)2=(x+y)2﹣4xy=25,
则x﹣y=±5;
(4)(2m+n)(m+n)=2m(m+n)+n(m+n)=2m2+3mn+n2.
26.解:(1)第一个图形中阴影部分的面积是a2﹣b2,第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故答案是B;
(2)①∵9x2﹣4y2=(3x+2y)(3x﹣2y),
∴24=6(x﹣2y)
得:3x﹣2y=4;
②原式=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+),
=×××××…××××,
=×,
=.
27.解:(1)根据题意,大矩形的面积为:(a+b+c)(a+b+c)=(a+b+c)2,
各小矩形部分的面积之和=a2+2ab+b2+2bc+2ac+c2,
∴等式为(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)a2+b2+c2 =(a+b+c)2﹣2ab﹣2ac﹣2bc=112﹣2×38=45.
(3)如图所示
28.解:(1)∵9=52﹣42,
∴9是“明礼崇德数”,
故答案为:是;
(2)∵(x2+y)与x2是P的一个平方差分解,
∴P=(x2+y)2﹣(x2)2
=x4+2x2y+y2﹣x4
=2x2y+y2;
(3)当k+5=0时,N为“明礼崇德数”,理由如下:
∵N=x2﹣y2+4x﹣6y+k=(x2+4x+4)﹣(y2+6y+9)+k+5=(x+2)2﹣(y+3)2+k+5,
∴当k+5=0时,N=(x+2)2﹣(y+3)2为“明礼崇德数”,
此时k=﹣5,
故当k=﹣5时,N为“明礼崇德数”.
29.解:(1)长方形ABCD的面积为30×(4×3+9)=630;
S1﹣S2=(30﹣9)×4×3﹣(30﹣3×3)×9=63;
故答案为:630,63;
(2)S1﹣S2=4b(40﹣a)﹣a(40﹣3b)
=160b﹣4ab﹣40a+3ab
=160b﹣ab﹣40a;
(3)∵S1﹣S2=4b(AD﹣a)﹣a(AD﹣3b),
整理,得:S1﹣S2=(4b﹣a)AD﹣ab,
∵S1﹣S2的值与AD的值无关,
∴4b﹣a=0,
解得:a=4b.
即a,b满足的关系是a=4b.
一.选择题
1.计算(a﹣2b)2=( )
A.a2﹣4ab+4b2 B.a2+4ab+4b2 C.a2﹣4ab﹣4b2 D.a2+4ab﹣4b2
2.在下列各项中,可以用平方差公式计算的是( )
A.(2a+3b)(3a﹣2b) B.(a+b)(﹣a﹣b)
C.(﹣m+n)(m﹣n) D.(a+b)(b﹣a)
3.下列运算中正确的是( )
A.(x+2)(x﹣2)=x2﹣2 B.(﹣3a﹣2)(3a﹣2)=4﹣9a2
C.(a+b)2=a2+b2 D.(a﹣b)2=a2﹣ab+b2
4.若(a+b)2=10,a2+b2=4,则ab的值为( )
A.14 B.7 C.6 D.3
5.图(1)是一个长为a,宽为b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是( )
A.a2 B.b2 C.(a﹣b)2 D.(a﹣b)2
6.如果x2﹣kxy+9y2是一个完全平方式,那么k的值是( )
A.3 B.±6 C.6 D.±3
7.计算(15x2y﹣10xy2)÷5xy的结果为( )
A.3x﹣2xy B.3xy﹣2y C.3x﹣2y D.3x2﹣2y2
8.如图甲,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形如图乙,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2
D.a2﹣b2=(a+b)(a﹣b)
二.填空题
9.计算:(x4﹣4x3)÷x2= .
10.已知(x+y)2=18,xy=5,则x2+y2的值为 .
11.若多项式4x2﹣kx+25是一个完全平方式,则k的值是 .
12.若a﹣b=8,ab=2,则a2+b2的值为 .
13.已知(a+b)2=7,(a﹣b)2=3,则ab= .
14.小明在计算一个二项式的平方时,得到的正确结果是4x2+12xy+■,但最后一项不慎被污染了,这一项应是 .
15.数学课上老师让同学们用若干个小矩形,拼成一个大矩形,如图所示,请你仔细观察图形,写出图中所表示的整式的乘法关系式为 .
16.已知a>0,b>0,(3a+3b+1)(3a+3b﹣1)=899,则a+b= .
17.当一个正方形的边长增加5cm时,它的面积增加85cm2,则原来正方形的边长是 cm.
18.小丽在计算3×(4+1)×(42+1)时,把3写成(4﹣1)后,发现可以连续运用平方差公式进行计算.用类似方法计算:(1+)×(1+)×(1+)×(1+)+= .
三.解答题
19.计算:(x﹣2y)(x+2y)﹣(x+2y)2.
20.计算:
(1)(3x+1)(x﹣2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
21.已知(x+y)2=25,(x﹣y)2=1,求x2+y2与xy的值.
22.先化简,再求值:(2m+1)(2m﹣1)﹣(m﹣1)2+(2m)3÷(﹣8m),其中m2+m﹣2=0.
23.先化简,再求值:(a﹣b)2﹣2a(a+3b)+(a+2b)(a﹣2b),其中a=1,b=﹣3.
24.已知多项式A=x2+2x+n2,多项式B=2x2+4x+3n2+3.
(1)若多项式x2+2x+n2是完全平方式,则n= ;
(2)已知x=m时,多项式x2+2x+n2的值为﹣1,则x=﹣m时,该多项式的值为多少?
(3)判断多项式A与B的大小关系并说明理由.
25.图1,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中的阴影部分的面积为 ;
(2)观察图2,三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系是 ;
(3)若x+y=﹣6,xy=2.75,求x﹣y;
(4)观察图3,你能得到怎样的代数恒等式呢?
26.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2+ab=a(a+b)
(2)应用:利用你从(1)选出的等式,完成下列各题:
①已知9x2﹣4y2=24,3x+2y=6,求3x﹣2y的值;
②计算:.
27.阅读下列文字,我们知道对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片.若干个长为a和宽为b的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:2a2+5ab+2b2=(2a+b)(a+2b).
28.阅读下列材料:
若一个正整数x能表示成a2﹣b2(a,b是正整数,且a>b)的形式,则称这个数为“明礼崇德数”,a与b是x的一个平方差分解.例如:因为5=32﹣22,所以5是“明礼崇德数”,3与2是5的平方差分解;再如:M=x2+2xy=x2+2xy+y2﹣y2=(x+y)2﹣y2(x,y是正整数),所以M也是“明礼崇德数”,(x+y)与y是M的一个平方差分解.
(1)判断:9 “明礼崇德数”(填“是”或“不是”);
(2)已知(x2+y)与x2是P的一个平方差分解,求P;
(3)已知N=x2﹣y2+4x﹣6y+k(x,y是正整数,k是常数,且x>y+1),要使N是“明礼崇德数”,试求出符合条件的一个k值,并说明理由.
29.将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S1﹣S2的值为 ;
(2)当AD=40时,请用含a、b的式子表示S1﹣S2的值;
(3)若AB长度保持不变,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,当a、b满足什么关系时,S1﹣S2的值与AD的长度无关?
参考答案
一.选择题
1.解:原式=a2﹣2a 2b+(2b)2
=a2﹣4ab+4b2,
故选:A.
2.解:A、(2a+3b)(3a﹣2b),不符合平方差公式的结构特征,故错误;
B、(a+b)(﹣a﹣b),不符合平方差公式的结构特征,故错误;
C、(﹣m+n)(m﹣n),不符合平方差公式的结构特征,故错误;
D、,符合平方差公式的结构特征,故正确;
故选:D.
3.解:A、(x+2)(x﹣2)=x2﹣4,错误;
B、(﹣3a﹣2)(3a﹣2)=4﹣9a2,正确;
C、(a+b)2=a2+2ab+b2,错误;
D、(a﹣b)2=a2﹣2ab+b2,错误;
故选:B.
4.解:∵(a+b)2=10,a2+b2=4,(a+b)2=a2+2ab+b2,
∴ab=[(a+b)2﹣(a2+b2)]=×(10﹣4)=3.
故选:D.
5.解:由题意得所剪得的每个小长方形的长为,宽为,
∴中间空余的部分的是一个边长为﹣的正方形,
∴中间空余的部分的面积是()2.
故选:D.
6.解:∵x2﹣kxy+9y2是一个完全平方式,
∴k=±6.
故选:B.
7.解:原式=15x2y÷5xy﹣10xy2÷5xy
=3x﹣2y,
故选:C.
8.解:图甲的面积=大正方形的面积﹣空白处正方形的面积=a2﹣b2;
图乙中矩形的长=a+b,宽=a﹣b,图乙的面积=(a+b)(a﹣b).
所以a2﹣b2=(a+b)(a﹣b).
故选:D.
二.填空题
9.解:原式=x4÷x2﹣4x3÷x2
=x2﹣4x,
故答案为:x2﹣4x.
10.解:∵(x+y)2=18,xy=5,
∴x2+y2+2xy=x2+y2+10=18.
∴x2+y2=8.
故答案为:8.
11.解:∵4x2﹣kx+25是一个完全平方式,
∴4x2﹣kx+25=(2x)2﹣kx+52=(2x±5)2,
∵(2x±5)2=4x2±20x+25,
∴﹣kx=±20x,解得k=±20.
故答案为:±20.
12.解:∵a﹣b=8,ab=2,
∴a2+b2=(a﹣b)2+2ab=64+4=68.
故答案为:68.
13.解:(a+b)2﹣(a﹣b)2=4ab=7﹣3=4,
所以可得:ab=1,
故答案为:1
14.解:∵4x2+12xy+■是一个二项式的平方,
∴■=(3y)2=9y2.
故答案为:9y2.
15.解:由拼图可得,大长方形的长为a+2b,宽为a+b,
所以面积为(a+2b)(a+b),
根据各个部分面积和为a2+3ab+2b2,
因此有(a+2b)(a+b)=a2+3ab+2b2,
故答案为:(a+2b)(a+b)=a2+3ab+2b2.
16.解:∵(3a+3b+1)(3a+3b﹣1)=899,
∴(3a+3b)2﹣1=899,
即(3a+3b)2=900,
又∵(±30)2=900,a>0,b>0,
∴3a+3b=30,
即a+b=10,
故答案为:10.
17.解:设原正方形边长为xcm,则增加后边长为(x+5)cm,
根据题意列方程得:(x+5)2﹣x2=85,
整理得10x+25=85,
解得x=6,
∴原来正方形边长为6cm.
故答案为:6.
18.解:(1+)×(1+)×(1+)×(1+)+
=
=×
=
=
=
=
=2.
故答案为:2.
三.解答题
19.解:(x﹣2y)(x+2y)﹣(x+2y)2
=(x2﹣4y2)﹣(x2+4y2+4xy)
=x2﹣4y2﹣x2﹣4y2﹣4xy
=﹣8y2﹣4xy.
20.解:(1)原式=3x2﹣6x+x﹣2
=3x2﹣5x﹣2;
(2)原式=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
21.解:∵(x+y)2=x2+2xy+y2=25①,(x﹣y)2=x2﹣2xy+y2=1②,
∴①+②得:2(x2+y2)=26,即x2+y2=13;
①﹣②得:4xy=24,即xy=6.
22.解:原式=4m2﹣1﹣(m2﹣2m+1)+8m3÷(﹣8m)
=4m2﹣1﹣m2+2m﹣1﹣m2
=2m2+2m﹣2
=2(m2+m)﹣2,
∵m2+m﹣2=0,
∴m2+m=2,
当m2+m=2时,原式=2×2﹣2=2.
23.解:原式=a2﹣2ab+b2﹣2a2﹣6ab+a2﹣4b2=﹣8ab﹣3b2.
当a=1、b=﹣3时,
原式=﹣8×1×(﹣3)﹣3×(﹣3)2
=24﹣27
=﹣3.
24.解:(1)∵x2+2x+n2是一个完全平方式,
∴n2=1,
∴n=±1.
故答案为:1或﹣1;
(2)当x=m时m2+2m+n2=﹣1,
∴m2+2m+1+n2=0,
∴(m+1)2+n2=0,
∵(m+1)2≥0,n2≥0,
∴x=m=﹣1,n=0,
∴x=﹣m时,多项式x2+2x+n2的值为m2﹣2m+n2=3;
(3)B>A.
理由如下:B﹣A=2x2+4x+3n2+3﹣(x2+2x+n2)=x2+2x+2n2+3=(x+1)2+2n2+2,
∵(x+1)2≥0,2n2≥0,
∴(x+1)2+2n2+2>0,
∴B>A.
25.解:(1)图②中的阴影部分的面积为(m﹣n)2,
故答案为:(m﹣n)2;
(2)(m+n)2﹣4mn=(m﹣n)2,
故答案为:(m+n)2﹣4mn=(m﹣n)2;
(3)(x﹣y)2=(x+y)2﹣4xy=25,
则x﹣y=±5;
(4)(2m+n)(m+n)=2m(m+n)+n(m+n)=2m2+3mn+n2.
26.解:(1)第一个图形中阴影部分的面积是a2﹣b2,第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故答案是B;
(2)①∵9x2﹣4y2=(3x+2y)(3x﹣2y),
∴24=6(x﹣2y)
得:3x﹣2y=4;
②原式=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+),
=×××××…××××,
=×,
=.
27.解:(1)根据题意,大矩形的面积为:(a+b+c)(a+b+c)=(a+b+c)2,
各小矩形部分的面积之和=a2+2ab+b2+2bc+2ac+c2,
∴等式为(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)a2+b2+c2 =(a+b+c)2﹣2ab﹣2ac﹣2bc=112﹣2×38=45.
(3)如图所示
28.解:(1)∵9=52﹣42,
∴9是“明礼崇德数”,
故答案为:是;
(2)∵(x2+y)与x2是P的一个平方差分解,
∴P=(x2+y)2﹣(x2)2
=x4+2x2y+y2﹣x4
=2x2y+y2;
(3)当k+5=0时,N为“明礼崇德数”,理由如下:
∵N=x2﹣y2+4x﹣6y+k=(x2+4x+4)﹣(y2+6y+9)+k+5=(x+2)2﹣(y+3)2+k+5,
∴当k+5=0时,N=(x+2)2﹣(y+3)2为“明礼崇德数”,
此时k=﹣5,
故当k=﹣5时,N为“明礼崇德数”.
29.解:(1)长方形ABCD的面积为30×(4×3+9)=630;
S1﹣S2=(30﹣9)×4×3﹣(30﹣3×3)×9=63;
故答案为:630,63;
(2)S1﹣S2=4b(40﹣a)﹣a(40﹣3b)
=160b﹣4ab﹣40a+3ab
=160b﹣ab﹣40a;
(3)∵S1﹣S2=4b(AD﹣a)﹣a(AD﹣3b),
整理,得:S1﹣S2=(4b﹣a)AD﹣ab,
∵S1﹣S2的值与AD的值无关,
∴4b﹣a=0,
解得:a=4b.
即a,b满足的关系是a=4b.
