湘教版八年级数学上册第1章分式 单元综合测试题 (含解析)
文档属性
| 名称 | 湘教版八年级数学上册第1章分式 单元综合测试题 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 249.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 00:00:00 | ||
图片预览

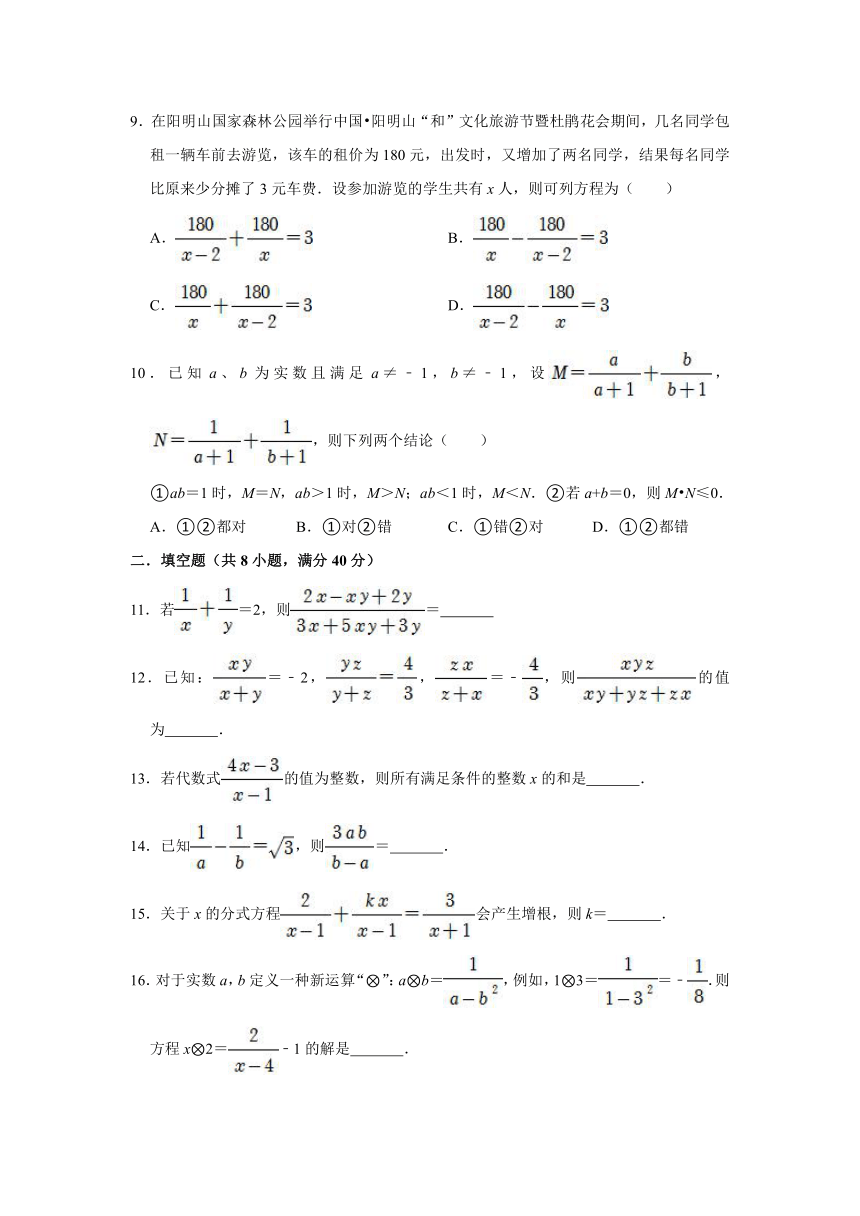



文档简介
2022-2023学年湘教版八年级数学上册《第1章分式》单元综合测试题(附答案)
一.选择题(共10小题,满分40分)
1.下列式子是分式的是( )
A.x B. C. D.
2.使分式的值为整数的全体自然数x的和是( )
A.5 B.6 C.12 D.22
3.分式方程的解是( )
A.x=3 B.x=﹣3 C.x1=﹣3,x2=2 D.x1=3,x2=2
4.如图,若x为正整数,则表示﹣的值的点落在( )
A.段① B.段② C.段③ D.段④
5.对于实数a、b,定义一种新运算“ ”为:a b=,这里等式右边是通常的四则运算,若(﹣3) x=2,则x的值为( )
A.﹣2 B.﹣ C. D.﹣
6.设x=+1,则=( )
A.3 B.4 C.5 D.8
7.若关于x的分式方程有增根,则k的值是( )
A. B.﹣1 C.1 D.
8.从﹣3,﹣2,﹣1,﹣,1,3这六个数中,随机抽取一个数,记为a.关于x的方程=1的解是正数,那么这6个数中所有满足条件的a的值有( )个.
A.3 B.2 C.1 D.4
9.在阳明山国家森林公园举行中国 阳明山“和”文化旅游节暨杜鹃花会期间,几名同学包租一辆车前去游览,该车的租价为180元,出发时,又增加了两名同学,结果每名同学比原来少分摊了3元车费.设参加游览的学生共有x人,则可列方程为( )
A. B.
C. D.
10.已知a、b为实数且满足a≠﹣1,b≠﹣1,设,,则下列两个结论( )
①ab=1时,M=N,ab>1时,M>N;ab<1时,M<N.②若a+b=0,则M N≤0.
A.①②都对 B.①对②错 C.①错②对 D.①②都错
二.填空题(共8小题,满分40分)
11.若=2,则=
12.已知:=﹣2,,=﹣,则的值为 .
13.若代数式的值为整数,则所有满足条件的整数x的和是 .
14.已知,则= .
15.关于x的分式方程会产生增根,则k= .
16.对于实数a,b定义一种新运算“ ”:a b=,例如,1 3==﹣.则方程x 2=﹣1的解是 .
17.已知关于x的方程的解大于1,则实数m的取值范围是 .
18.若关于x的方程=无解,则a的值是 .
三.解答题(共5小题,满分40分)
19.计算:
(1); (2)﹣a﹣1.
20.先化简,再求值:(+x﹣2)÷,其中|x|=2.
21.定义:若两个分式的差为2,则称这两个分式属于“友好分式组”.
(1)下列3组分式:
①与;②与;③与.其中属于“友好分式组”的有 (只填序号);
(2)若正实数a,b互为倒数,求证,分式与属于“友好分式组”;
(3)若a,b均为非零实数,且分式与属于“友好分式组”,求分式的值.
22.已知关于x的方程.
(1)若m=﹣3,解这个分式方程;
(2)若原分式方程无解,求m的值.
23.根据规划设计,某工程队准备修建一条长1000m的公路.由于采取新的施工方式,实际每天修建公路的长度比原计划增加20m,从而缩短了工期.假设原计划每天修建公路am,那么
(1)原计划修建这条公路需要多少天?实际修建这条公路用了多少天?
(2)实际修建这条公路的工期比原计划缩短了几天?
参考答案
一.选择题(共10小题,满分40分)
1.解:A.x是整式,故A不符合题意;
B.是整式,故B不符合题意;
C.是分式,故C符合题意;
D.是整式,故D不符合题意;
故选:C.
2.解:由于原式=x﹣1+,为使为整数,
则自然数x可取0,1,2,3,5,11,其和为22.
故选:D.
3.解:方程两边都乘以最简公分母(x+2)(x﹣2)得,
(x+2)2﹣(3x+10)=0,
x2+4x+4﹣3x﹣10=0,
x2+x﹣6=0,
(x+3)(x﹣2)=0,
x+3=0,x﹣2=0,
解得x1=﹣3,x2=2,
检验:当x=﹣3时,(x+2)(x﹣2)=(﹣3+2)(﹣3﹣2)=5≠0,
当x=2时,(x+2)(x﹣2)=(﹣2+2)(﹣2﹣2)=0,
所以x=﹣3是分式方程的解,
故原分式方程的解是x=﹣3.
故选:B.
4.解∵﹣=﹣=1﹣=
又∵x为正整数,
∴≤<1
故表示﹣的值的点落在②
故选:B.
5.解:∵a b=,且(﹣3) x=2,
∴=2
∴2(9+3x)=3
∴6x=﹣15
∴x=﹣
经检验,x=﹣是原方程的解.
故选:B.
6.解:∵(﹣1)(+1)=﹣13=5﹣1=4,x=+1,
∴=[+1]3,
=(﹣1+1)3,
=5.
故选:C.
7.解:∵分式方程有增根,
∴x﹣5=0,
解得x=5,
原方程化为:
+1=,
x﹣6+x﹣5=﹣2k,
2x﹣11=﹣2k,
把x=5代入2x﹣11=﹣2k得,
10﹣11=﹣2k,
解得k=.
故选:D.
8.解:由=1得:2x+a=x﹣1
∴x=﹣1﹣a
∵解是正数,且x﹣1为原方程的分母,
∴﹣1﹣a>0,且﹣1﹣a≠1
∴a<﹣1,且a≠﹣2
故在﹣3,﹣2,﹣1,﹣,1,3这六个数中,符合题意得数有:﹣3,﹣,
故选:B.
9.解:设实际参加游览的同学共x人,
根据题意得:.
故选:D.
10.解:∵,,
∴M﹣N=﹣(),
=,
=,
=,
①当ab=1时,M﹣N=0,
∴M=N,
当ab>1时,
∴2ab>2,
∴2ab﹣2>0,
当a<0时,b<0,(a+1)(b+1)>0或(a+1)(b+1)<0,
∴M﹣N>0或M﹣N<0,
∴M>N或M<N;
当ab<1时,ab可能同号,也可能异号,
∴(a+1)(b+1)>0或(a+1)(b+1)<0,
∵2ab﹣a<0,
∴M>N或M<N;
∴①不正确;
②M N=() ()
=++,
∵a+b=0
∴原式=
=
=
∵a≠﹣1,b≠﹣1,∴(a+1)2(b+1)2>0,
∵a+b=0
∴ab≤0,M N≤0.
∴②对.
故选:C.
二.填空题(共8小题,满分40分)
11.解:由=2,得x+y=2xy
则===.
故答案为.
12.解:∵=﹣2,,=﹣
∴+=﹣,+=,+=﹣
∴++=﹣
则==﹣4.
故答案为:﹣4.
13.解:==4+,
∵代数式的值为整数,x为整数,
∴x﹣1=±1,
解得x=2或x=0,
则所有满足条件的整数x的和是2.
故答案为:2.
14.解:∵
∴===
故答案为:.
15.解:方程两边都乘(x+1)(x﹣1),得
2(x+1)+kx=3(x﹣1),即(k﹣1)x=﹣5,
∵最简公分母为(x+1)(x﹣1),
∴原方程增根为x=±1,
∴把x=1代入整式方程,得k=﹣4.
把x=﹣1代入整式方程,得k=6.
综上可知k=﹣4或6.
故答案为:﹣4或6
16.解:根据题中的新定义,化简得:=﹣1,
去分母得:1=2﹣x+4,
解得:x=5,
经检验,x=5是分式方程的解,
故答案为:x=5.
17.解:方程两边乘x﹣2得:x+m=2﹣x,
移项得:2x=2﹣m,
系数化为1得:x=,
∵方程的解大于1,
∴>1,且≠2,解得m<0,且m≠﹣2.
故答案为:m<0,且m≠﹣2.
18.解:分式方程去分母,可得
a(x+1)=2x,
即(a﹣2)x=﹣a,
当a=2时,方程(a﹣2)x=﹣a无解;
当a≠2时,若x=1,则a﹣2=﹣a,即a=1;
若x=﹣1,则2﹣a=﹣a(无解);
综上所述,a=2或1,
故答案为:2或1.
三.解答题(共5小题,满分40分)
19.解:(1)
=
=
=;
(2)﹣a﹣1
=
=
=.
20.解:原式=÷
=
=,
∵|x|=2时,
∴x=±2,
由分式有意义的条件可知:x=2,
∴原式=3.
21.解:(1)①﹣=≠2,
②﹣==2,
③|﹣|=||=2,
∴属于“友好分式组”的有②③,
故答案为:②③.
(2)∵a,b互为倒数,
∴ab=1,b=,
∴|﹣|
=|﹣|
=|﹣|
=||
=2,
∴分式与属于“友好分式组”;
(3)∵|﹣|
=|﹣|
=||
=||,
∵与属于“友好分式组”,
∴||=2,
∴2a2+2ab=2(a2﹣4b2)或2a2+2ab=﹣2(a2﹣4b2),
①a=﹣4b,②ab=4b2﹣2a2,
把①代入==﹣,
把②代入==﹣,
综上所述:的值为﹣或﹣.
22.解:①依题意把m=﹣3代入原方程得.
方程两边都乘最简公分母(x﹣3)(x+3)得,
﹣3(x﹣3)+(x+3)=1.
解得x=5.5.
检验:把x=5.5代入(x+3)(x﹣3)≠0.
∴x=5.5是原方程的解.
②当(x+3)(x﹣3)=0时.x=±3.
方程两边都乘最简公分母(x﹣3)(x+3),得.
m(x﹣3)+(x+3)=m+4.
整理得(m+1)x=1+4m
∵原分式方程无解.
∴m+1=0,m=﹣1.
把x=±3代入m(x﹣3)+(x+3)=m+4.
m=2,m=﹣.
∴m=﹣1,m=2,m=﹣
23.解:(1)原计划修建这条公路需要天,实际修建这条公路用了天;
(2)实际修建这条公路的工期比原计划缩短了(﹣)天.
一.选择题(共10小题,满分40分)
1.下列式子是分式的是( )
A.x B. C. D.
2.使分式的值为整数的全体自然数x的和是( )
A.5 B.6 C.12 D.22
3.分式方程的解是( )
A.x=3 B.x=﹣3 C.x1=﹣3,x2=2 D.x1=3,x2=2
4.如图,若x为正整数,则表示﹣的值的点落在( )
A.段① B.段② C.段③ D.段④
5.对于实数a、b,定义一种新运算“ ”为:a b=,这里等式右边是通常的四则运算,若(﹣3) x=2,则x的值为( )
A.﹣2 B.﹣ C. D.﹣
6.设x=+1,则=( )
A.3 B.4 C.5 D.8
7.若关于x的分式方程有增根,则k的值是( )
A. B.﹣1 C.1 D.
8.从﹣3,﹣2,﹣1,﹣,1,3这六个数中,随机抽取一个数,记为a.关于x的方程=1的解是正数,那么这6个数中所有满足条件的a的值有( )个.
A.3 B.2 C.1 D.4
9.在阳明山国家森林公园举行中国 阳明山“和”文化旅游节暨杜鹃花会期间,几名同学包租一辆车前去游览,该车的租价为180元,出发时,又增加了两名同学,结果每名同学比原来少分摊了3元车费.设参加游览的学生共有x人,则可列方程为( )
A. B.
C. D.
10.已知a、b为实数且满足a≠﹣1,b≠﹣1,设,,则下列两个结论( )
①ab=1时,M=N,ab>1时,M>N;ab<1时,M<N.②若a+b=0,则M N≤0.
A.①②都对 B.①对②错 C.①错②对 D.①②都错
二.填空题(共8小题,满分40分)
11.若=2,则=
12.已知:=﹣2,,=﹣,则的值为 .
13.若代数式的值为整数,则所有满足条件的整数x的和是 .
14.已知,则= .
15.关于x的分式方程会产生增根,则k= .
16.对于实数a,b定义一种新运算“ ”:a b=,例如,1 3==﹣.则方程x 2=﹣1的解是 .
17.已知关于x的方程的解大于1,则实数m的取值范围是 .
18.若关于x的方程=无解,则a的值是 .
三.解答题(共5小题,满分40分)
19.计算:
(1); (2)﹣a﹣1.
20.先化简,再求值:(+x﹣2)÷,其中|x|=2.
21.定义:若两个分式的差为2,则称这两个分式属于“友好分式组”.
(1)下列3组分式:
①与;②与;③与.其中属于“友好分式组”的有 (只填序号);
(2)若正实数a,b互为倒数,求证,分式与属于“友好分式组”;
(3)若a,b均为非零实数,且分式与属于“友好分式组”,求分式的值.
22.已知关于x的方程.
(1)若m=﹣3,解这个分式方程;
(2)若原分式方程无解,求m的值.
23.根据规划设计,某工程队准备修建一条长1000m的公路.由于采取新的施工方式,实际每天修建公路的长度比原计划增加20m,从而缩短了工期.假设原计划每天修建公路am,那么
(1)原计划修建这条公路需要多少天?实际修建这条公路用了多少天?
(2)实际修建这条公路的工期比原计划缩短了几天?
参考答案
一.选择题(共10小题,满分40分)
1.解:A.x是整式,故A不符合题意;
B.是整式,故B不符合题意;
C.是分式,故C符合题意;
D.是整式,故D不符合题意;
故选:C.
2.解:由于原式=x﹣1+,为使为整数,
则自然数x可取0,1,2,3,5,11,其和为22.
故选:D.
3.解:方程两边都乘以最简公分母(x+2)(x﹣2)得,
(x+2)2﹣(3x+10)=0,
x2+4x+4﹣3x﹣10=0,
x2+x﹣6=0,
(x+3)(x﹣2)=0,
x+3=0,x﹣2=0,
解得x1=﹣3,x2=2,
检验:当x=﹣3时,(x+2)(x﹣2)=(﹣3+2)(﹣3﹣2)=5≠0,
当x=2时,(x+2)(x﹣2)=(﹣2+2)(﹣2﹣2)=0,
所以x=﹣3是分式方程的解,
故原分式方程的解是x=﹣3.
故选:B.
4.解∵﹣=﹣=1﹣=
又∵x为正整数,
∴≤<1
故表示﹣的值的点落在②
故选:B.
5.解:∵a b=,且(﹣3) x=2,
∴=2
∴2(9+3x)=3
∴6x=﹣15
∴x=﹣
经检验,x=﹣是原方程的解.
故选:B.
6.解:∵(﹣1)(+1)=﹣13=5﹣1=4,x=+1,
∴=[+1]3,
=(﹣1+1)3,
=5.
故选:C.
7.解:∵分式方程有增根,
∴x﹣5=0,
解得x=5,
原方程化为:
+1=,
x﹣6+x﹣5=﹣2k,
2x﹣11=﹣2k,
把x=5代入2x﹣11=﹣2k得,
10﹣11=﹣2k,
解得k=.
故选:D.
8.解:由=1得:2x+a=x﹣1
∴x=﹣1﹣a
∵解是正数,且x﹣1为原方程的分母,
∴﹣1﹣a>0,且﹣1﹣a≠1
∴a<﹣1,且a≠﹣2
故在﹣3,﹣2,﹣1,﹣,1,3这六个数中,符合题意得数有:﹣3,﹣,
故选:B.
9.解:设实际参加游览的同学共x人,
根据题意得:.
故选:D.
10.解:∵,,
∴M﹣N=﹣(),
=,
=,
=,
①当ab=1时,M﹣N=0,
∴M=N,
当ab>1时,
∴2ab>2,
∴2ab﹣2>0,
当a<0时,b<0,(a+1)(b+1)>0或(a+1)(b+1)<0,
∴M﹣N>0或M﹣N<0,
∴M>N或M<N;
当ab<1时,ab可能同号,也可能异号,
∴(a+1)(b+1)>0或(a+1)(b+1)<0,
∵2ab﹣a<0,
∴M>N或M<N;
∴①不正确;
②M N=() ()
=++,
∵a+b=0
∴原式=
=
=
∵a≠﹣1,b≠﹣1,∴(a+1)2(b+1)2>0,
∵a+b=0
∴ab≤0,M N≤0.
∴②对.
故选:C.
二.填空题(共8小题,满分40分)
11.解:由=2,得x+y=2xy
则===.
故答案为.
12.解:∵=﹣2,,=﹣
∴+=﹣,+=,+=﹣
∴++=﹣
则==﹣4.
故答案为:﹣4.
13.解:==4+,
∵代数式的值为整数,x为整数,
∴x﹣1=±1,
解得x=2或x=0,
则所有满足条件的整数x的和是2.
故答案为:2.
14.解:∵
∴===
故答案为:.
15.解:方程两边都乘(x+1)(x﹣1),得
2(x+1)+kx=3(x﹣1),即(k﹣1)x=﹣5,
∵最简公分母为(x+1)(x﹣1),
∴原方程增根为x=±1,
∴把x=1代入整式方程,得k=﹣4.
把x=﹣1代入整式方程,得k=6.
综上可知k=﹣4或6.
故答案为:﹣4或6
16.解:根据题中的新定义,化简得:=﹣1,
去分母得:1=2﹣x+4,
解得:x=5,
经检验,x=5是分式方程的解,
故答案为:x=5.
17.解:方程两边乘x﹣2得:x+m=2﹣x,
移项得:2x=2﹣m,
系数化为1得:x=,
∵方程的解大于1,
∴>1,且≠2,解得m<0,且m≠﹣2.
故答案为:m<0,且m≠﹣2.
18.解:分式方程去分母,可得
a(x+1)=2x,
即(a﹣2)x=﹣a,
当a=2时,方程(a﹣2)x=﹣a无解;
当a≠2时,若x=1,则a﹣2=﹣a,即a=1;
若x=﹣1,则2﹣a=﹣a(无解);
综上所述,a=2或1,
故答案为:2或1.
三.解答题(共5小题,满分40分)
19.解:(1)
=
=
=;
(2)﹣a﹣1
=
=
=.
20.解:原式=÷
=
=,
∵|x|=2时,
∴x=±2,
由分式有意义的条件可知:x=2,
∴原式=3.
21.解:(1)①﹣=≠2,
②﹣==2,
③|﹣|=||=2,
∴属于“友好分式组”的有②③,
故答案为:②③.
(2)∵a,b互为倒数,
∴ab=1,b=,
∴|﹣|
=|﹣|
=|﹣|
=||
=2,
∴分式与属于“友好分式组”;
(3)∵|﹣|
=|﹣|
=||
=||,
∵与属于“友好分式组”,
∴||=2,
∴2a2+2ab=2(a2﹣4b2)或2a2+2ab=﹣2(a2﹣4b2),
①a=﹣4b,②ab=4b2﹣2a2,
把①代入==﹣,
把②代入==﹣,
综上所述:的值为﹣或﹣.
22.解:①依题意把m=﹣3代入原方程得.
方程两边都乘最简公分母(x﹣3)(x+3)得,
﹣3(x﹣3)+(x+3)=1.
解得x=5.5.
检验:把x=5.5代入(x+3)(x﹣3)≠0.
∴x=5.5是原方程的解.
②当(x+3)(x﹣3)=0时.x=±3.
方程两边都乘最简公分母(x﹣3)(x+3),得.
m(x﹣3)+(x+3)=m+4.
整理得(m+1)x=1+4m
∵原分式方程无解.
∴m+1=0,m=﹣1.
把x=±3代入m(x﹣3)+(x+3)=m+4.
m=2,m=﹣.
∴m=﹣1,m=2,m=﹣
23.解:(1)原计划修建这条公路需要天,实际修建这条公路用了天;
(2)实际修建这条公路的工期比原计划缩短了(﹣)天.
同课章节目录
