人教版七年级上册1.5.1乘方课件(共21张PPT)
文档属性
| 名称 | 人教版七年级上册1.5.1乘方课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 459.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 13:40:17 | ||
图片预览








文档简介
(共21张PPT)
1.5有理数的乘方
1.5.1 乘方
*
你喜欢吃拉面吗?拉面馆的师傅用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,这样捏合20次后能拉出多少根细面条?
想一想
第一次
捏合后
第二次
捏合后
第三次
捏合后
…
*
读作a的平方或a的二次方
探索新知
读作a的立方或a 的三次方
读作a 的四次方
=an
a×a ×… ×a ×a
n个
读作a的n次方
an
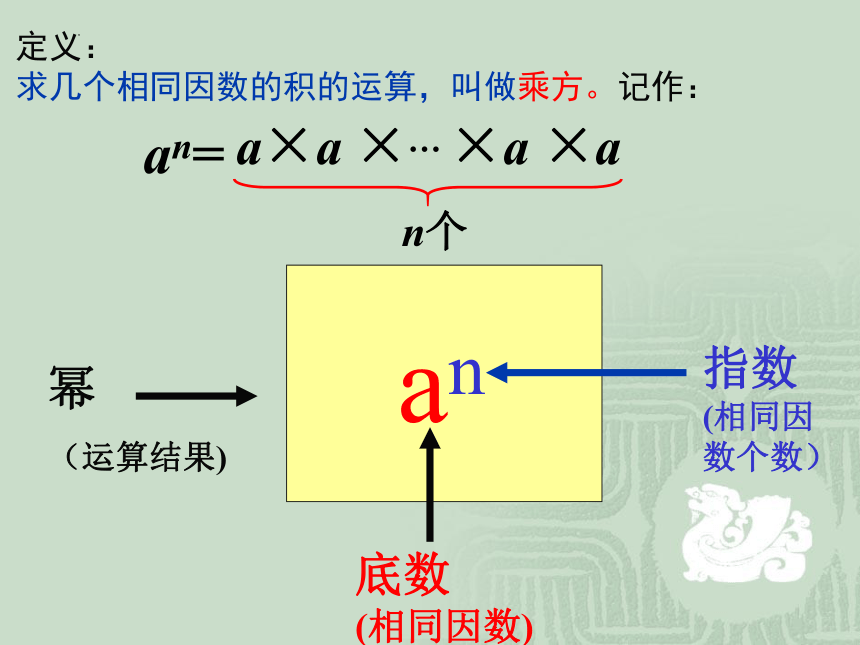
指数
(相同因数个数)
底数
(相同因数)
幂
(运算结果)
*
定义:
求几个相同因数的积的运算,叫做乘方。记作:
an=
a×a ×… ×a ×a
n个
练习:把下列式子写成乘方的形式,并指出它们的指数和底数。
1、9×9×9×9=
2、(-2)×(-2)×(-2)×(-2)=
3、
*
=
注意:底数是负数或分数的乘方,书写时一定要把整个负数或分数(连同符号)用括号括起来.
94
(-2)4
思考:
(-2)4与-24一样吗?有什么不同?
*
(-2)4表示4个-2的乘积,读作负2的四次方
-24表示4个2的乘积的相反数,读作负的2的四次方
做一做: 计算
(1)102 103
(2)
=100
=1000
=10000
=100
=-1000
=10000
(3)
=0.01
=0.001
=0.0001
=0.00001
(4)(-0.1) (-0.1) (-0.1) (-0.1)
=0.01
=-0.001
=0.0001
=-0.00001
(-10)
=-100000
10
=100000
10
例1 计算:
(1) (-4)3 ; (2) (-2)4; (3)
解:(1)(-4)3=(-4)×(-4)×(-4)=-64;
(2)(-2)4=(-2)×(-2)×(-2)×(-2)=16;
(3) = 。
*
思考
你发现负数的幂的正负有什么规律?
*
当指数是偶数时,负数的幂是正数;
当指数是奇数时,负数的幂是负数。
符号法则:
正数的任何次幂都是正数;
负数的偶次幂是正数;
负数的奇次幂是负数。
乘方运算的步骤:
1、先定符号;
2、再算绝对值的积。
*
1、(-1)1 ,(-1)2 ,(-1)3 ,(-1)4 ,(-1)100,(-1)101
*
(-1)1 =-1 (-1)2=1 (-1)3 =-1(-1)4 =1
(-1)100 =1 (-1)101 =-1
-1的奇数次幂是-1,-1的偶数次幂是1。
2、 1的任何次幂有什么特征
1的任何次幂都是1。
运用新知 体会成功:
(1)、(-5)3 (2)、
(3)、23 (4)、(10)3
(5)、(-1)2
(6)、08
-125
256
81
8
1000
1
0
*
例2:用计算器计算
解:用带符号键 的计算器.
(-)
(-)
(
9
∧
=
531 441.
(-)
(
7
∧
=
-16807.
显示:(-9)∧6
显示:(-7)∧5
)
6
)
5
*
用计算器计算:
262 144
-279 936
20 736
9 924.36543
练一练
归纳
*
运算名称 运算结果
加法 和
减法 差
乘法 积
除法 商
乘方 幂
做有理数的混合运算时,应注意以下运算顺序:
1、先乘方,再乘除,最后加减;
2、同级运算,从左到右进行;
3、如有括号,按小括号、中括号、大括号依次进行。
例3、计算:
①
②
解:
原式
原式
*
与乘方有关的规律探索问题
例4 观察下面三行数:
-2,4,-8,16,-32,64,...;
0,6,-6,18,-30,66,...;
-1,2,-4,8,-16,32,...;
(1)第 行数按什么规律排列?
(2)第 行数与第 行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和。
总结提升
有关乘方的规律探索
1.对于乘方运算的规律探索,一般从符号和绝对值两个方面入手分析.
2.对运算的结果或表达的形式进行观察分析,由特殊到一般归纳得出规律.
*
请你说说这节课学到了什么
作业:
. 1、
2、(1)、(2)、(3)、(7)、(8)
3、(3)、(4)
思考题:将一张1毫米的纸对折多少次后,高达三米?
*
练习
3
1.5有理数的乘方
1.5.1 乘方
*
你喜欢吃拉面吗?拉面馆的师傅用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,这样捏合20次后能拉出多少根细面条?
想一想
第一次
捏合后
第二次
捏合后
第三次
捏合后
…
*
读作a的平方或a的二次方
探索新知
读作a的立方或a 的三次方
读作a 的四次方
=an
a×a ×… ×a ×a
n个
读作a的n次方
an
指数
(相同因数个数)
底数
(相同因数)
幂
(运算结果)
*
定义:
求几个相同因数的积的运算,叫做乘方。记作:
an=
a×a ×… ×a ×a
n个
练习:把下列式子写成乘方的形式,并指出它们的指数和底数。
1、9×9×9×9=
2、(-2)×(-2)×(-2)×(-2)=
3、
*
=
注意:底数是负数或分数的乘方,书写时一定要把整个负数或分数(连同符号)用括号括起来.
94
(-2)4
思考:
(-2)4与-24一样吗?有什么不同?
*
(-2)4表示4个-2的乘积,读作负2的四次方
-24表示4个2的乘积的相反数,读作负的2的四次方
做一做: 计算
(1)102 103
(2)
=100
=1000
=10000
=100
=-1000
=10000
(3)
=0.01
=0.001
=0.0001
=0.00001
(4)(-0.1) (-0.1) (-0.1) (-0.1)
=0.01
=-0.001
=0.0001
=-0.00001
(-10)
=-100000
10
=100000
10
例1 计算:
(1) (-4)3 ; (2) (-2)4; (3)
解:(1)(-4)3=(-4)×(-4)×(-4)=-64;
(2)(-2)4=(-2)×(-2)×(-2)×(-2)=16;
(3) = 。
*
思考
你发现负数的幂的正负有什么规律?
*
当指数是偶数时,负数的幂是正数;
当指数是奇数时,负数的幂是负数。
符号法则:
正数的任何次幂都是正数;
负数的偶次幂是正数;
负数的奇次幂是负数。
乘方运算的步骤:
1、先定符号;
2、再算绝对值的积。
*
1、(-1)1 ,(-1)2 ,(-1)3 ,(-1)4 ,(-1)100,(-1)101
*
(-1)1 =-1 (-1)2=1 (-1)3 =-1(-1)4 =1
(-1)100 =1 (-1)101 =-1
-1的奇数次幂是-1,-1的偶数次幂是1。
2、 1的任何次幂有什么特征
1的任何次幂都是1。
运用新知 体会成功:
(1)、(-5)3 (2)、
(3)、23 (4)、(10)3
(5)、(-1)2
(6)、08
-125
256
81
8
1000
1
0
*
例2:用计算器计算
解:用带符号键 的计算器.
(-)
(-)
(
9
∧
=
531 441.
(-)
(
7
∧
=
-16807.
显示:(-9)∧6
显示:(-7)∧5
)
6
)
5
*
用计算器计算:
262 144
-279 936
20 736
9 924.36543
练一练
归纳
*
运算名称 运算结果
加法 和
减法 差
乘法 积
除法 商
乘方 幂
做有理数的混合运算时,应注意以下运算顺序:
1、先乘方,再乘除,最后加减;
2、同级运算,从左到右进行;
3、如有括号,按小括号、中括号、大括号依次进行。
例3、计算:
①
②
解:
原式
原式
*
与乘方有关的规律探索问题
例4 观察下面三行数:
-2,4,-8,16,-32,64,...;
0,6,-6,18,-30,66,...;
-1,2,-4,8,-16,32,...;
(1)第 行数按什么规律排列?
(2)第 行数与第 行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和。
总结提升
有关乘方的规律探索
1.对于乘方运算的规律探索,一般从符号和绝对值两个方面入手分析.
2.对运算的结果或表达的形式进行观察分析,由特殊到一般归纳得出规律.
*
请你说说这节课学到了什么
作业:
. 1、
2、(1)、(2)、(3)、(7)、(8)
3、(3)、(4)
思考题:将一张1毫米的纸对折多少次后,高达三米?
*
练习
3
