1.4.2 第1课时 有理数的减法 课件(共24页)
文档属性
| 名称 | 1.4.2 第1课时 有理数的减法 课件(共24页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 08:22:09 | ||
图片预览






文档简介
(共24张PPT)
1.4 有理数的加法和减法
1.4.2 有理数的减法
第1课时 有理数的减法
湘教版七年级上册
教学目标
1.理解、掌握有理数的减法法则,会将有理数的减法运算转化为加法运算.(重点、难点)
2.通过把有理数的减法运算转化为加法运算,渗透转化思想,培养运算能力.
周日
2 ~ 9℃
周三
-1~ 6℃
周五
-4 ~ - 3℃
周一
0~ 8℃
周六
-5 ~ 5℃
周二
1 ~ 7℃
周四
-2 ~ -5℃
下面是某市未来一周的天气预报:
导入新课
情境引入
周六
-5 ~ 5℃
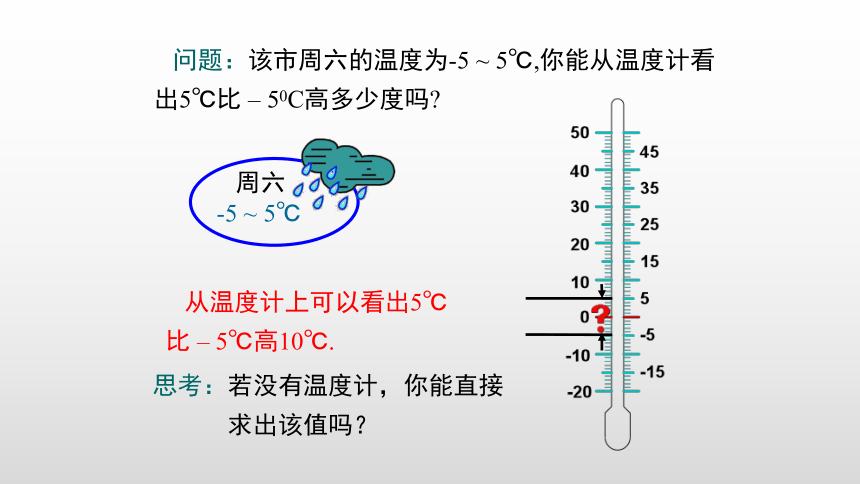
问题:该市周六的温度为-5 ~ 5℃,你能从温度计看出5℃比 – 50C高多少度吗
从温度计上可以看出5℃比 – 5℃高10℃.
思考:若没有温度计,你能直接
求出该值吗?
讲授新课
有理数的减法法则
一
问题:若跳水运动员从3米板(记为+3)高处跳进泳池,一直到水下3米(记为-3)才停止下沉,那她一共经过的距离是多少?
3-(-3)=
减法是加法的逆运算,上式可变为 +(-3)=3
实质是做减法
因为6+(-3)=3,所以上式中 =6 ,即3-(-3)=6.
试一试:请根据提供的式子完成下列算式:
(-3)+(+10)= +7
( –2 )+ (–8)=-10
②(–10)–(–8)=
①(+7)-(+10)=
-3
-2
③(+7)+(-10)=
④(–10)+(+8)=
-3
-2
思考:算式①和②是什么运算?等式③和④是又是什么运算?结果怎样?
议一议:这两个等式有什么特点?从等式中同学们
对减法运算有什么认识?
发现:算式左边是减法运算;算式右边是加法运算;减法运算可以转化为加法运算.
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
减法计算过程演示:
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
减号变加号
减数变为相反数
减数变为相反数
减号变加号
你学会了吗?
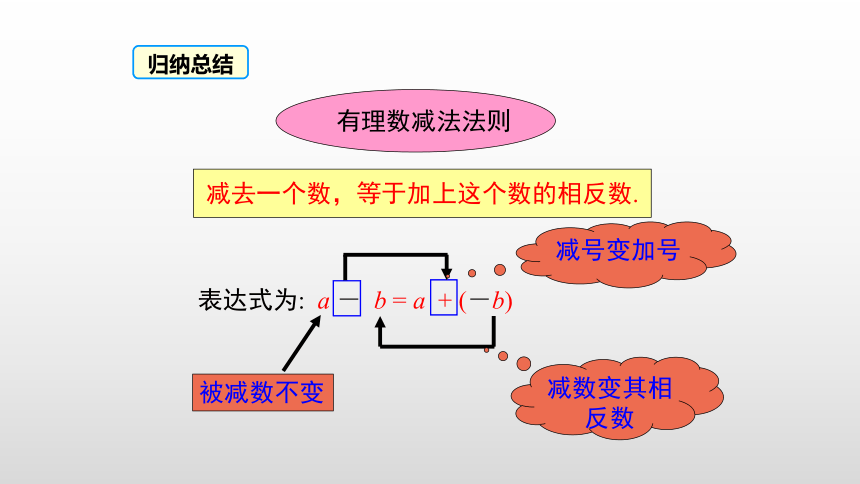
有理数减法法则
减去一个数,等于加上这个数的相反数.
表达式为: a - b = a + (-b)
减号变加号
减数变其相反数
被减数不变
归纳总结
1.填空:
(1)(-2)-(-3)=(-2)+( );
(2) 0 - (-4)= 0 +( );
(3)(-6)- 3 =(-6)+( );
(4) 1-(+39)= 1 +( ).
练一练
3
4
-3
-39
总结:
1.任何数减零仍得原数;
2.零减去一个数等于这个数的相反数.
(1)0 –8= (2)(-5 )– 0=
(3)30 – 0 = (4)0 – (–15) =
– 8
15
– 5
30
2.计算:
例1 计算:
解:
(1) 0-(-3.18)=0+3.18=3.18;
(2) 5.3-(-2.7)=5.3+2.7=8;
(3) (-10)-(-6)=(-10)+6=-4;
(1) 0-(-3.18); (2) 5.3-(-2.7);
(3)(-10)-(-6); (4) .
(4)
典例精析
(1)(-3)―(―5); (2)0-7;
(3)7.2―(―4.8); (4)-3
-5
解:(1) (-3)―(―5)= (-3)+5=2
计算:
(2) 0-7 = 0+(-7) =-7
(3) 7.2―(―4.8) = 7.2+4.8 = 12
(4) -3 -5 =-3 +(-5 )=-8
练一练
例2 世界上最高的山峰是珠穆朗玛峰,其海拔高度是 8848 米,吐鲁番盆地的海拔高度是–155 米,两处高度相差多少米?
解:8848-(-155)
=8848+155
=9003(米)
答:两处高度相差9003米.
有理数减法的应用
二
例3 某次法律知识竞赛中规定:抢答题答对一题得20分,答错一题扣10分,问答对一题与答错一题得分相差多少分?
解:
20-(-10)=20+10=30(分)
即答对一题与答错一题相差30分.
有理数减法在实际应用中的四个步骤:
1.审:审清题意;
2.列:列出正确的算式;
3.算:按照减法运算法则,进行正确的计算;
4.答:写出实际问题的答案.
归纳总结
例4 有理数a,b在数轴上的位置如图所示,试判断a-b的符号.
解:因为a在原点左边,所以a<0.
因为b在原点右边,所以b>0,
所以a-b=a+(-b)<0.
差的符号讨论:对于任意有理数a,b,有:①若a>b,则a-b>0;②若a=b,则a-b=0;③若a<b,则a-b<0,反之亦成立,据此可联想到用作差法来比较有理数的大小.
总结
【变式】 已知有理数a<0,b<0,且|a|>|b|,试判定a-b的符号.
解:因为a<0,b<0,所以-b>0.
又因为a-b=a+(-b),
所以a与-b是异号两数相加,
那么它们和的符号由绝对值较大的加数的符号决定,
因为|a|>|b|,即|a|>|-b|,
所以取a的符号,而a<0,
因此a-b的符号为负号.
(1)(+7) -(-4)=_______ ;
(2)(-0.45)-(-0.55)=_______ ;
(3) 0-(-9)=________;
(4)(-4)- 0=________ ;
(5)(-5)-(+3)=_________.
1.计算:
当堂练习
11
0.1
9
-4
-8
2.填空:
(1)温度4℃比-6℃高________℃ ;
(2)温度-7℃比-2℃低_________℃ ;
(3)海拔高度-13m比-200m高_______m;
(4)从海拔20m到-40m,下降了______m.
10
5
187
60
4.下列说法中不正确的是( )
A.两个数的差一定小于被减数
B.若两个数的差为0,则这两数必相等
C.零减去一个数一定得负数
D.一个负数减去一个负数结果仍是负数
3.下面等式正确的是( )
A.a-b=(-a)+ b B.a-(-b)=(-a)+(-b)
C.(-a)-(-b)=(-a)+(-b) D.a-(-b)=a+b
D
B
课堂小结
有理数减法法则
一般法则
应用
a-b = a +(-b)
特殊法则
0-b =-b;b-0 =b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4 有理数的加法和减法
1.4.2 有理数的减法
第1课时 有理数的减法
湘教版七年级上册
教学目标
1.理解、掌握有理数的减法法则,会将有理数的减法运算转化为加法运算.(重点、难点)
2.通过把有理数的减法运算转化为加法运算,渗透转化思想,培养运算能力.
周日
2 ~ 9℃
周三
-1~ 6℃
周五
-4 ~ - 3℃
周一
0~ 8℃
周六
-5 ~ 5℃
周二
1 ~ 7℃
周四
-2 ~ -5℃
下面是某市未来一周的天气预报:
导入新课
情境引入
周六
-5 ~ 5℃
问题:该市周六的温度为-5 ~ 5℃,你能从温度计看出5℃比 – 50C高多少度吗
从温度计上可以看出5℃比 – 5℃高10℃.
思考:若没有温度计,你能直接
求出该值吗?
讲授新课
有理数的减法法则
一
问题:若跳水运动员从3米板(记为+3)高处跳进泳池,一直到水下3米(记为-3)才停止下沉,那她一共经过的距离是多少?
3-(-3)=
减法是加法的逆运算,上式可变为 +(-3)=3
实质是做减法
因为6+(-3)=3,所以上式中 =6 ,即3-(-3)=6.
试一试:请根据提供的式子完成下列算式:
(-3)+(+10)= +7
( –2 )+ (–8)=-10
②(–10)–(–8)=
①(+7)-(+10)=
-3
-2
③(+7)+(-10)=
④(–10)+(+8)=
-3
-2
思考:算式①和②是什么运算?等式③和④是又是什么运算?结果怎样?
议一议:这两个等式有什么特点?从等式中同学们
对减法运算有什么认识?
发现:算式左边是减法运算;算式右边是加法运算;减法运算可以转化为加法运算.
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
减法计算过程演示:
(+7)-(+10)=
(+7)+(-10)
(–10)–(–8)=
(–10)+(+8)
减号变加号
减数变为相反数
减数变为相反数
减号变加号
你学会了吗?
有理数减法法则
减去一个数,等于加上这个数的相反数.
表达式为: a - b = a + (-b)
减号变加号
减数变其相反数
被减数不变
归纳总结
1.填空:
(1)(-2)-(-3)=(-2)+( );
(2) 0 - (-4)= 0 +( );
(3)(-6)- 3 =(-6)+( );
(4) 1-(+39)= 1 +( ).
练一练
3
4
-3
-39
总结:
1.任何数减零仍得原数;
2.零减去一个数等于这个数的相反数.
(1)0 –8= (2)(-5 )– 0=
(3)30 – 0 = (4)0 – (–15) =
– 8
15
– 5
30
2.计算:
例1 计算:
解:
(1) 0-(-3.18)=0+3.18=3.18;
(2) 5.3-(-2.7)=5.3+2.7=8;
(3) (-10)-(-6)=(-10)+6=-4;
(1) 0-(-3.18); (2) 5.3-(-2.7);
(3)(-10)-(-6); (4) .
(4)
典例精析
(1)(-3)―(―5); (2)0-7;
(3)7.2―(―4.8); (4)-3
-5
解:(1) (-3)―(―5)= (-3)+5=2
计算:
(2) 0-7 = 0+(-7) =-7
(3) 7.2―(―4.8) = 7.2+4.8 = 12
(4) -3 -5 =-3 +(-5 )=-8
练一练
例2 世界上最高的山峰是珠穆朗玛峰,其海拔高度是 8848 米,吐鲁番盆地的海拔高度是–155 米,两处高度相差多少米?
解:8848-(-155)
=8848+155
=9003(米)
答:两处高度相差9003米.
有理数减法的应用
二
例3 某次法律知识竞赛中规定:抢答题答对一题得20分,答错一题扣10分,问答对一题与答错一题得分相差多少分?
解:
20-(-10)=20+10=30(分)
即答对一题与答错一题相差30分.
有理数减法在实际应用中的四个步骤:
1.审:审清题意;
2.列:列出正确的算式;
3.算:按照减法运算法则,进行正确的计算;
4.答:写出实际问题的答案.
归纳总结
例4 有理数a,b在数轴上的位置如图所示,试判断a-b的符号.
解:因为a在原点左边,所以a<0.
因为b在原点右边,所以b>0,
所以a-b=a+(-b)<0.
差的符号讨论:对于任意有理数a,b,有:①若a>b,则a-b>0;②若a=b,则a-b=0;③若a<b,则a-b<0,反之亦成立,据此可联想到用作差法来比较有理数的大小.
总结
【变式】 已知有理数a<0,b<0,且|a|>|b|,试判定a-b的符号.
解:因为a<0,b<0,所以-b>0.
又因为a-b=a+(-b),
所以a与-b是异号两数相加,
那么它们和的符号由绝对值较大的加数的符号决定,
因为|a|>|b|,即|a|>|-b|,
所以取a的符号,而a<0,
因此a-b的符号为负号.
(1)(+7) -(-4)=_______ ;
(2)(-0.45)-(-0.55)=_______ ;
(3) 0-(-9)=________;
(4)(-4)- 0=________ ;
(5)(-5)-(+3)=_________.
1.计算:
当堂练习
11
0.1
9
-4
-8
2.填空:
(1)温度4℃比-6℃高________℃ ;
(2)温度-7℃比-2℃低_________℃ ;
(3)海拔高度-13m比-200m高_______m;
(4)从海拔20m到-40m,下降了______m.
10
5
187
60
4.下列说法中不正确的是( )
A.两个数的差一定小于被减数
B.若两个数的差为0,则这两数必相等
C.零减去一个数一定得负数
D.一个负数减去一个负数结果仍是负数
3.下面等式正确的是( )
A.a-b=(-a)+ b B.a-(-b)=(-a)+(-b)
C.(-a)-(-b)=(-a)+(-b) D.a-(-b)=a+b
D
B
课堂小结
有理数减法法则
一般法则
应用
a-b = a +(-b)
特殊法则
0-b =-b;b-0 =b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
