11.1.1 平方根 课件(21张PPT)
文档属性
| 名称 | 11.1.1 平方根 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
11.1.1 平方根
华师大版 八年级上册
教学目标
【教学重点】理解平方根与算术平方根概念;会求一个正数的平方根.
【教学难点】算术平方根的非负性与算术平方根的特征.
1.理解并掌握平方根与算术平方根的概念.
2.理解平方运算与开平方的互逆关系.
3.理解算术平方根的非负性,会用计算器求一个数的算术平方根.
新知导入
问题1:已知一幅正方形的油画的面积是25cm2,这幅油画的边长是多少?
( )2=25.
5
x2=25
x =
新知导入
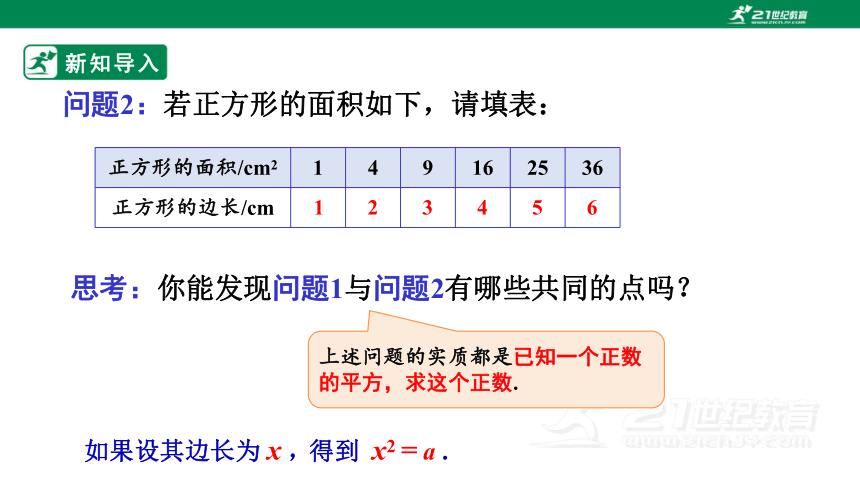
问题2:若正方形的面积如下,请填表:
正方形的面积/cm2 1 4 9 16 25 36
正方形的边长/cm
1
2
3
4
5
6
思考:你能发现问题1与问题2有哪些共同的点吗?
上述问题的实质都是已知一个正数的平方,求这个正数.
如果设其边长为 x ,
得到 x2 = a .
新知讲解
概括
如果一个数的平方等于a,那么这个数叫做a的平方根.
在问题1中,因为52=25,所以5是25的平方根.
25的平方根只有一个吗?还有没有别的数的平方也等于25?
又因为(-5)2=25,所以-5也是25的一个平方根.
根据平方根的意义,我们可以利用平方运算来求一个数的平方根.
典例讲解
例1 求100的平方根.
解: 因为102=100,(-10) 2=100,
除了10和-10以外,任何数的平方都不等于100,
所以100的平方根是10和-10.
也可以说,100的平方根是土10.
试一试:求下列各数的平方根
⑴ 9 ⑵ 0.49 ⑶ 1.69
⑷ ⑸ 2
新知讲解
试
一
试
(1)144的平方根是什么?
(2)0的平方根是什么?
(3)-4有没有平方根?为什么?
±12
0
没有,因为一个数的平方不可能是负数.
通过这些题目的解答,你能发现什么?
思考:正数有几个平方根?0有几个平方根?负数呢?
新知讲解
平方根的情况:
⑴一个正数的平方根有两个,
它们是互为相反数;
⑵ 0的平方根只有一个,
就是它本身0;
⑶负数没有平方根.
概括
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
新知讲解
一个正数如果有平方根,那么必定有两个,它们互为相反数.显然,如果我们知道了这两个平方根中的一个,那么立即可以得到另一个.
概括
正数a的正的平方根,叫做a的算术平方根,记作 ,读作“根号a”;另一个平方根是它的相反数,即 .因此,正数a的平方根可以记作 ,其中a称为被开方数.
特殊:0的算术平方根是0. 记作 .
新知讲解
根号
被开方数
a是非负数,a≥0.
求一个非负数的平方根的运算,叫做开平方.将一个正数开平方,关键是找出它的算术平方根.
在例1中,我们可以先求出100的算术平方根是 ,然后得知100的平方根是 .
平方与开平方有什么关系?
平方与开平方互为逆运算
例题讲解
例2 将下列各数开平方:
(1) 49 (2)
解
(1)因为72 = 49,所以 = 7,
因此49的平方根为士 =士7.
(2)因为 = ,所以 = ,
因此 的平方根为士 =士
新知讲解
问题3:将2016开平方运算的结果是多少?如何计算呢?
对于较大的数,或无法直接找到平方等于某个数时,可以借助计算器来求一个数的算术平方根(有时会是近似值).
计算器计算算术平方根的方法:
在计算器上依次键入:
被开方数
=
典例讲解
例3 用计算器求下列各数的算术平方根:
(1) 529;
(2) 44. 81(精确到0.01 ).
说明:用计算器求一个正数的算术平方根,只需直接按书写顺序按键即可.
典例讲解
解:(1) 在计算器上依次键入
5 2 9 =
显示结果为23,所以529的算术平方根为
= 23。
(2)在计算器上依次键入
4 4 . 8 1 =
显示结果为____, 要求精确到0.01,可得
≈____。
课堂总结
平方根
定义
性质
正数有两个平方根,它们互为相反数.
0的平方根是0.
负数没有平方根.
算术平方根
开平方
随堂练习
填一填
1. 平方根恰是本身的数是_____; 算术平方根恰是本
身的数是______.
0
0
、1
2. 4的平方是_____; 4的平方根是_____.
16
±2
3
±2
3. 9的算术平方根是_____; 的平方根是_____.
√16
4. =_____; - =_____; ± =____.
√36
√25
√49
5
-6
±7
5. 81的算术平方根是____; (-9)2的平方根是____.
9
81
±9
6. 若x2=9, 则x =____; 若 =9 , 则x =____;
√x2
若 =9, 则x =____.
√x
7. 若一个正数的两个平方根是m和m-4, 则m =____;
且这个正数值是____.
±3
±9
2
4
拓展提高
1、已知一个正数的平方根是2a-1和a-5,求这个正数。
拓展提高
2、已知2m+2的平方根是±4,3m+n+1的平方根是±5,求m+2n的值。
拓展提高
3、求下列各式中x的值.
(1)3x2=48 (1)(x+1)2=4 (1)2(x-1)2-18=0
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.1.1 平方根
华师大版 八年级上册
教学目标
【教学重点】理解平方根与算术平方根概念;会求一个正数的平方根.
【教学难点】算术平方根的非负性与算术平方根的特征.
1.理解并掌握平方根与算术平方根的概念.
2.理解平方运算与开平方的互逆关系.
3.理解算术平方根的非负性,会用计算器求一个数的算术平方根.
新知导入
问题1:已知一幅正方形的油画的面积是25cm2,这幅油画的边长是多少?
( )2=25.
5
x2=25
x =
新知导入
问题2:若正方形的面积如下,请填表:
正方形的面积/cm2 1 4 9 16 25 36
正方形的边长/cm
1
2
3
4
5
6
思考:你能发现问题1与问题2有哪些共同的点吗?
上述问题的实质都是已知一个正数的平方,求这个正数.
如果设其边长为 x ,
得到 x2 = a .
新知讲解
概括
如果一个数的平方等于a,那么这个数叫做a的平方根.
在问题1中,因为52=25,所以5是25的平方根.
25的平方根只有一个吗?还有没有别的数的平方也等于25?
又因为(-5)2=25,所以-5也是25的一个平方根.
根据平方根的意义,我们可以利用平方运算来求一个数的平方根.
典例讲解
例1 求100的平方根.
解: 因为102=100,(-10) 2=100,
除了10和-10以外,任何数的平方都不等于100,
所以100的平方根是10和-10.
也可以说,100的平方根是土10.
试一试:求下列各数的平方根
⑴ 9 ⑵ 0.49 ⑶ 1.69
⑷ ⑸ 2
新知讲解
试
一
试
(1)144的平方根是什么?
(2)0的平方根是什么?
(3)-4有没有平方根?为什么?
±12
0
没有,因为一个数的平方不可能是负数.
通过这些题目的解答,你能发现什么?
思考:正数有几个平方根?0有几个平方根?负数呢?
新知讲解
平方根的情况:
⑴一个正数的平方根有两个,
它们是互为相反数;
⑵ 0的平方根只有一个,
就是它本身0;
⑶负数没有平方根.
概括
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
新知讲解
一个正数如果有平方根,那么必定有两个,它们互为相反数.显然,如果我们知道了这两个平方根中的一个,那么立即可以得到另一个.
概括
正数a的正的平方根,叫做a的算术平方根,记作 ,读作“根号a”;另一个平方根是它的相反数,即 .因此,正数a的平方根可以记作 ,其中a称为被开方数.
特殊:0的算术平方根是0. 记作 .
新知讲解
根号
被开方数
a是非负数,a≥0.
求一个非负数的平方根的运算,叫做开平方.将一个正数开平方,关键是找出它的算术平方根.
在例1中,我们可以先求出100的算术平方根是 ,然后得知100的平方根是 .
平方与开平方有什么关系?
平方与开平方互为逆运算
例题讲解
例2 将下列各数开平方:
(1) 49 (2)
解
(1)因为72 = 49,所以 = 7,
因此49的平方根为士 =士7.
(2)因为 = ,所以 = ,
因此 的平方根为士 =士
新知讲解
问题3:将2016开平方运算的结果是多少?如何计算呢?
对于较大的数,或无法直接找到平方等于某个数时,可以借助计算器来求一个数的算术平方根(有时会是近似值).
计算器计算算术平方根的方法:
在计算器上依次键入:
被开方数
=
典例讲解
例3 用计算器求下列各数的算术平方根:
(1) 529;
(2) 44. 81(精确到0.01 ).
说明:用计算器求一个正数的算术平方根,只需直接按书写顺序按键即可.
典例讲解
解:(1) 在计算器上依次键入
5 2 9 =
显示结果为23,所以529的算术平方根为
= 23。
(2)在计算器上依次键入
4 4 . 8 1 =
显示结果为____, 要求精确到0.01,可得
≈____。
课堂总结
平方根
定义
性质
正数有两个平方根,它们互为相反数.
0的平方根是0.
负数没有平方根.
算术平方根
开平方
随堂练习
填一填
1. 平方根恰是本身的数是_____; 算术平方根恰是本
身的数是______.
0
0
、1
2. 4的平方是_____; 4的平方根是_____.
16
±2
3
±2
3. 9的算术平方根是_____; 的平方根是_____.
√16
4. =_____; - =_____; ± =____.
√36
√25
√49
5
-6
±7
5. 81的算术平方根是____; (-9)2的平方根是____.
9
81
±9
6. 若x2=9, 则x =____; 若 =9 , 则x =____;
√x2
若 =9, 则x =____.
√x
7. 若一个正数的两个平方根是m和m-4, 则m =____;
且这个正数值是____.
±3
±9
2
4
拓展提高
1、已知一个正数的平方根是2a-1和a-5,求这个正数。
拓展提高
2、已知2m+2的平方根是±4,3m+n+1的平方根是±5,求m+2n的值。
拓展提高
3、求下列各式中x的值.
(1)3x2=48 (1)(x+1)2=4 (1)2(x-1)2-18=0
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
