沪科版数学七年级上册 4.4角 课件(共18张)
文档属性
| 名称 | 沪科版数学七年级上册 4.4角 课件(共18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 19:14:09 | ||
图片预览




文档简介
(共18张PPT)
4.4 角
第4章 直线与角
知识要点
1.角的概念及表示方法
2.角的分类
3.角的度量与计算
新知导入
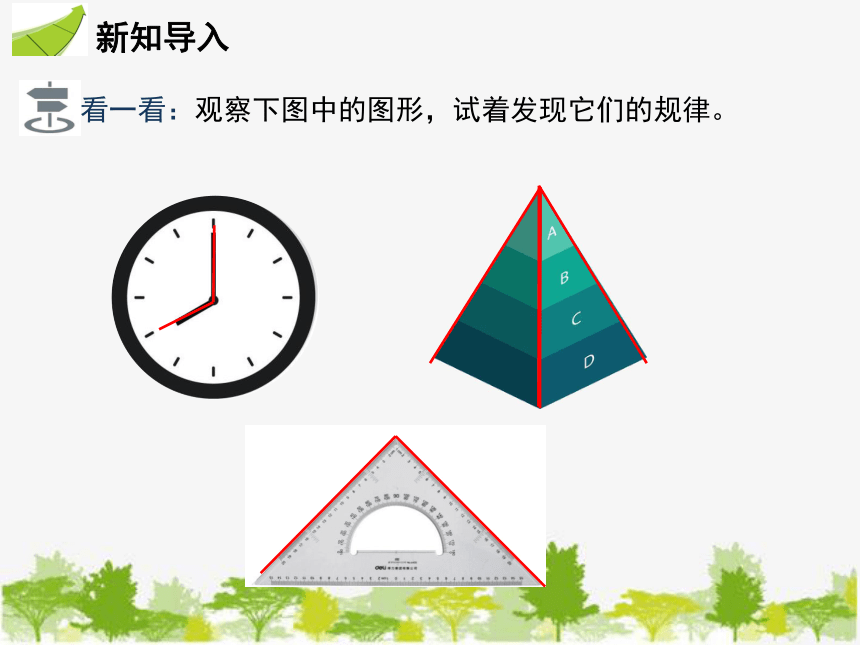
看一看:观察下图中的图形,试着发现它们的规律。
课程讲授
1
角的定义及表示方法
问题1:根据图中角的特点试着归纳出角的定义.
课程讲授
1
角的定义及表示方法
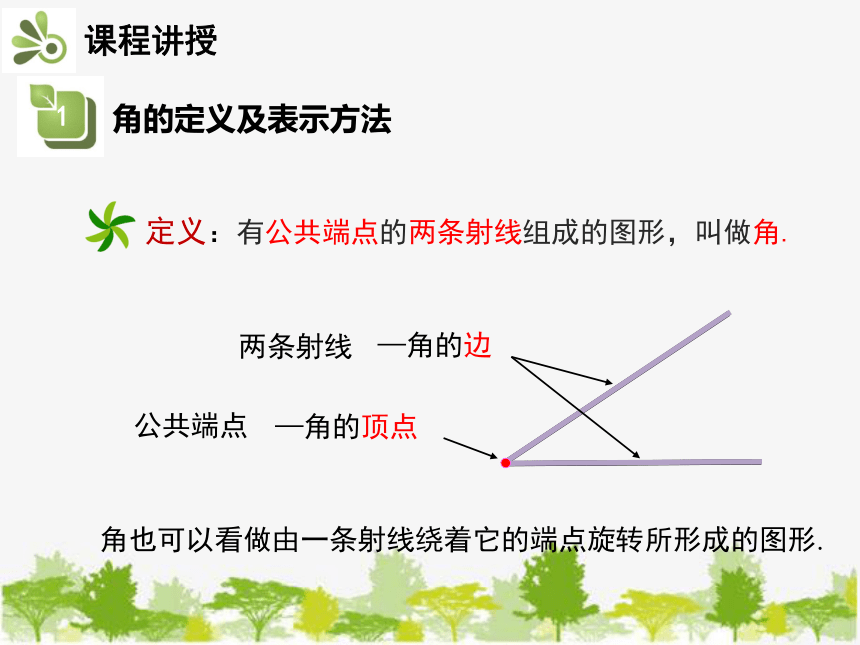
公共端点
—角的顶点
两条射线
—角的边
角也可以看做由一条射线绕着它的端点旋转所形成的图形.
定义:有公共端点的两条射线组成的图形,叫做角.
课程讲授
1
角的定义及表示方法
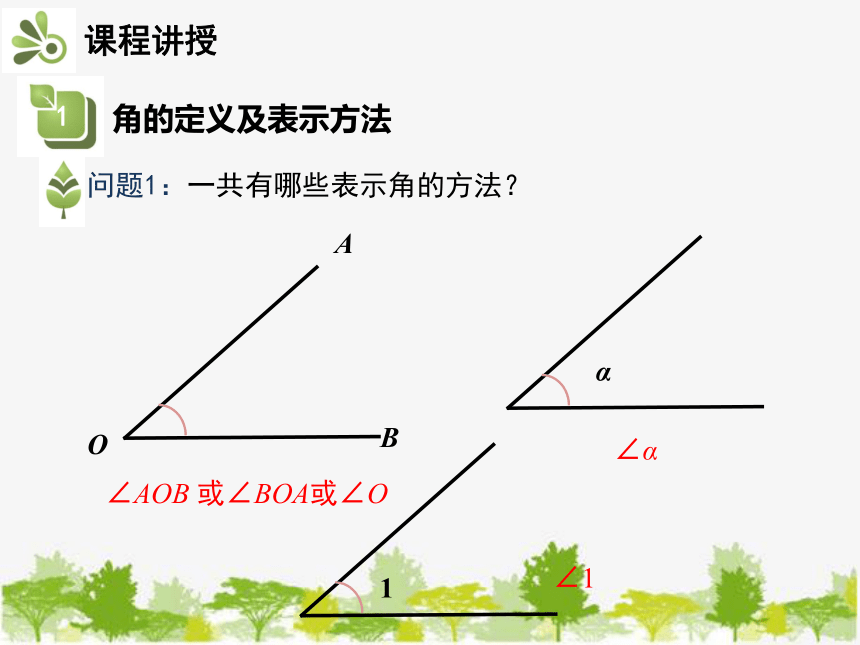
问题1:一共有哪些表示角的方法?
A
B
O
α
1
∠AOB 或∠BOA或∠O
∠α
∠1
课程讲授
1
角的定义及表示方法
练一练:下列说法中正确的是( )
A.两条射线所组成的图形叫做角
B.有公共点的两条射线叫做角
C.一条射线绕着它的端点旋转叫做角
D.一条射线绕着它的端点旋转所成的图形叫做角
D
课程讲授
2
角的分类
问题1:如何衡量一个角的大小?
课程讲授
2
角的分类
问题2:如何对角进行分类呢?
平角
直角
锐角
钝角
课程讲授
3
角的度量与计算
问题1:怎么知道这个角的大小?
A
B
O
角的度量工具:
量角器
课程讲授
3
角的度量与计算
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是 1 度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °
1°= ′;1′= ″.
360
180
60
60
课程讲授
3
角的度量与计算
例 计算:
(1)37°28′+ 24°35′; (2)83°20′-45°38′20″;
(3)25°53′28″×5; (4)15°20′÷6.
解:(1) 37°28′+ 24°35′
= 61°63′
= 62°3′;
解:(2) 83°20′- 45°38′20″
= 82°79′60″- 45°38′20″
= 37°41′40″.
课程讲授
3
角的度量与计算
例 计算:
(3)25°53′28″×5; (4)15°20′÷6.
解:(3)25°53′28″×5
=25°×5+53′×5+28″×5
=125°+265′+140″
=129°27′20″.
解:(4)15°20′÷6
=12°200′÷6
=12°÷6+200′÷6
=2°+198′÷6+2′÷6
=2°+33′+120″÷6
=2°33′20″.
课程讲授
练一练:将31.39°用度分秒表示,结果是( )
A.31°3′9″
B.31°23′4″
C.31°23′24″
D.31°23′
C
3
角的度量与计算
随堂练习
1.如图,下面说法正确的是( )
A.∠ABC和∠DAE是同一个角
B.∠ABC和∠C是同一个角
C.∠ADE可以用∠D表示
D.∠ABC可以用∠B表示
D
随堂练习
B
2.图中角的表示方法正确的个数有( )
A.1个
B.2个
C.3个
D.4个
随堂练习
3.从3时到6时,钟表的时针转过的角的度数是( )
A.30°
B.60°
C.90°
D.120°
C
课堂小结
角
角的概念及表示方法
角的定义:有公共端点的两条射线组成的图形,叫做角.
角的表示方法
角的分类
角的度量与计算
锐角
平角
角的度量工具:量角器
角的换算
1周角=360°;1平角=180°
1°=60′;1′=60″.
直角
钝角
4.4 角
第4章 直线与角
知识要点
1.角的概念及表示方法
2.角的分类
3.角的度量与计算
新知导入
看一看:观察下图中的图形,试着发现它们的规律。
课程讲授
1
角的定义及表示方法
问题1:根据图中角的特点试着归纳出角的定义.
课程讲授
1
角的定义及表示方法
公共端点
—角的顶点
两条射线
—角的边
角也可以看做由一条射线绕着它的端点旋转所形成的图形.
定义:有公共端点的两条射线组成的图形,叫做角.
课程讲授
1
角的定义及表示方法
问题1:一共有哪些表示角的方法?
A
B
O
α
1
∠AOB 或∠BOA或∠O
∠α
∠1
课程讲授
1
角的定义及表示方法
练一练:下列说法中正确的是( )
A.两条射线所组成的图形叫做角
B.有公共点的两条射线叫做角
C.一条射线绕着它的端点旋转叫做角
D.一条射线绕着它的端点旋转所成的图形叫做角
D
课程讲授
2
角的分类
问题1:如何衡量一个角的大小?
课程讲授
2
角的分类
问题2:如何对角进行分类呢?
平角
直角
锐角
钝角
课程讲授
3
角的度量与计算
问题1:怎么知道这个角的大小?
A
B
O
角的度量工具:
量角器
课程讲授
3
角的度量与计算
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是 1 度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °
1°= ′;1′= ″.
360
180
60
60
课程讲授
3
角的度量与计算
例 计算:
(1)37°28′+ 24°35′; (2)83°20′-45°38′20″;
(3)25°53′28″×5; (4)15°20′÷6.
解:(1) 37°28′+ 24°35′
= 61°63′
= 62°3′;
解:(2) 83°20′- 45°38′20″
= 82°79′60″- 45°38′20″
= 37°41′40″.
课程讲授
3
角的度量与计算
例 计算:
(3)25°53′28″×5; (4)15°20′÷6.
解:(3)25°53′28″×5
=25°×5+53′×5+28″×5
=125°+265′+140″
=129°27′20″.
解:(4)15°20′÷6
=12°200′÷6
=12°÷6+200′÷6
=2°+198′÷6+2′÷6
=2°+33′+120″÷6
=2°33′20″.
课程讲授
练一练:将31.39°用度分秒表示,结果是( )
A.31°3′9″
B.31°23′4″
C.31°23′24″
D.31°23′
C
3
角的度量与计算
随堂练习
1.如图,下面说法正确的是( )
A.∠ABC和∠DAE是同一个角
B.∠ABC和∠C是同一个角
C.∠ADE可以用∠D表示
D.∠ABC可以用∠B表示
D
随堂练习
B
2.图中角的表示方法正确的个数有( )
A.1个
B.2个
C.3个
D.4个
随堂练习
3.从3时到6时,钟表的时针转过的角的度数是( )
A.30°
B.60°
C.90°
D.120°
C
课堂小结
角
角的概念及表示方法
角的定义:有公共端点的两条射线组成的图形,叫做角.
角的表示方法
角的分类
角的度量与计算
锐角
平角
角的度量工具:量角器
角的换算
1周角=360°;1平角=180°
1°=60′;1′=60″.
直角
钝角
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
