密铺(课件)-四年级下册数学北师大版(共46张PPT)
文档属性
| 名称 | 密铺(课件)-四年级下册数学北师大版(共46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 11:00:01 | ||
图片预览











文档简介
(共46张PPT)
数学好玩
北师大版 四年级下册
1.通过观察、操作,理解图形密铺的特征,了解三角形和四边形具有密铺特点。
2.通过猜想、操作等活动发展空间想象能力和动手能力,培养创新意识。
3.通过欣赏、设计和展示交流活动,进一步感受图形密铺的奇妙,感受数学的美,体验参与数学学习活动的乐趣。
【重点】理解什么是图形密铺。
【难点】探索三角形和四边形是否可以密铺。
学习目标:
课前准备:三角形、梯形、一般四边形、正五边形、正六边形的卡片若干张。
俄罗斯方块
G D
OO
课前导入:
密铺
在装修时经常要在地面或墙面上铺砖,
下面是瓷砖常见的铺法。
这些图形是怎样拼在一起的?什么是密铺
请观察,这些图形在拼接时有什么特点
不留空隙、不重叠
请观察,这些图形在拼接时有什么特点
不留空隙、不重叠
什么是密铺:
(1)用一种或几种全等图形进行拼接。
(2)拼接处不留空隙、不重叠。
(3)能连续铺成一片。
平面图形密铺的特点:
把形状、大小相同的一种或几种平面图形不留空隙、不重叠的拼接在一起,这就是密铺。
活动任务
三角形能不能密铺?四边形可不可以?
设计方案:
1.设计实验的步骤。
(1)准备大小,形状完全相同的三角形、梯形和一般四边形的卡片若干张。
(2)一人负责用三角形拼摆,一人负责用梯形拼摆,一人负责用一般四边形拼摆。
(3)观察是否密铺。
解决这个问题需要哪些主要步骤?
1.将准备好的三角形、梯形和一般四边形拼一拼,摆一摆。
2.收集实验结果并记录。
形状 三角形 梯形 一般四边形
是否密铺
动手实验
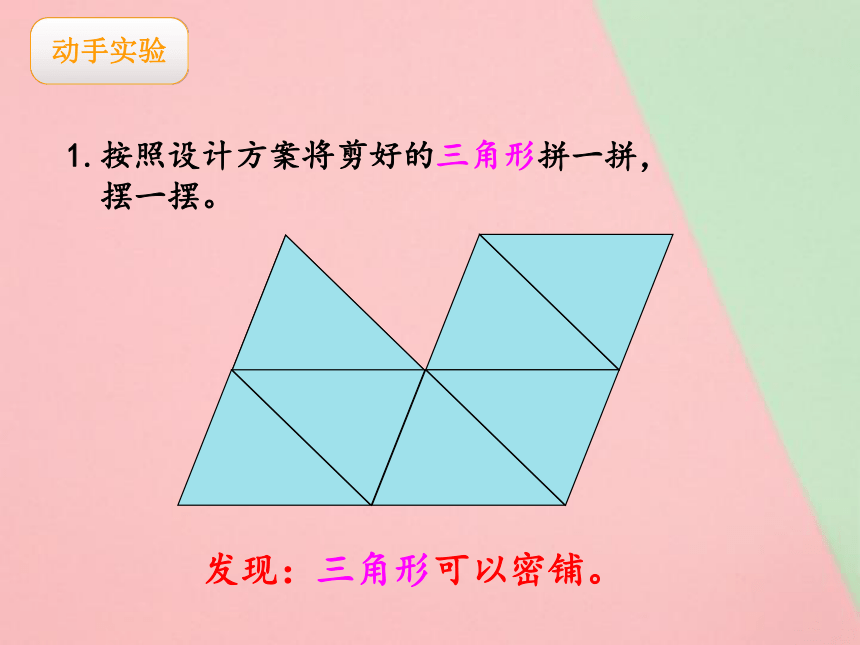
动手实验
1.按照设计方案将剪好的三角形拼一拼,
摆一摆。
发现:三角形可以密铺。
动手实验
1.按照设计方案将剪好的梯形拼一拼,
摆一摆。
发现:梯形可以密铺。
动手实验
1.按照设计方案将剪好的一般四边形拼一拼,
摆一摆。
发现:一般四边形可以密铺。
收集实验结果并记录。
形状 三角形 梯形 一般四边形
是否密铺
是
是
是
三角形和四边形都可以密铺
为什么可以呢
交流反思
1.请按照下面的方法试一试,你有什么发现?
我将相同图形的角按序号标好,密铺后发现……
三角形
梯形
一般四边形
结论:任意全等的三角形能密铺
三角形的每个内角在每个拼接点处出现两次,所以180°×2=360°
单独一种多边形密铺
周角
用形状、大小完全相同的任意四边形能否密铺?
四边形的每个内角在每个拼接点处出现一次,共:360°。
结论:任意全等的四边形能密铺
周角
2.在上面的活动中,你有什么收获?
密铺与图形的 角有关系。
密铺的图形中,拼接点处几个角的度数之和正好是360°
交流反思
3.不是所有的平面图形都可以密铺。看一看,试一
试。
正五边形
正六边形
啊!拼不了啦,为什么呢 你能说说原因吗
1
2
3
正五边形可以密铺吗?
108度
×( ?)
≠360度
108度
正五边形不可以密铺
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
120度
×3
=360度
120度
正六边形可以密铺
归纳小结:
三角形一定可以密铺.
正六边形可以密铺.
1.因为三角形的内角和是180°, 用几个全等三角形拼接时,每个角只需用两次,就能拼出一个周角,所以
2.任意四边形的四个内角之和是360°,而密铺时拼接点的四个角刚好能拼成一个周角,所以
任意四边形一定可以密铺.
3.正六边形的每个内角都是120°,也能拼接出周角,所以
结论:密铺与图形的角有关系,每个拼接点处,当几个多边形的内角和能组成360度时,则可以密铺,否则将无法进行密铺的。
(×)
(√)
(√)
(√)
(√)
(×)
三角形、四边形、正六边形可以进行单独密铺 。
圆形和正五边形不能进行单独密铺。
汇报:
1
当拼接点处的几个角的度数和为360°时,就能密铺。
单独一种多边形密铺
用同一种平面图形如果不能密铺, 用两种或者两种以上平面图形能不能密铺呢
两种多边形密铺探索
能
用同一种平面图形如果不能密铺, 用两种或者两种以上平面图形能不能密铺呢
能
这是密铺作品,这也是镶嵌,它是怎么样做出来的呢?
请往下看,实际上是很简单的
不规则图形密铺探索
你看懂了吗?实际上是用正方形“剪”“拼”出来的
用你掌握的知识来判断下面正多边形能否密铺.
正八边形(一个内角是135度)
正九边形(一个内角是140度)
正十边形(一个内角是144度)
不能密铺
不能密铺
不能密铺
1
135度x( )≠360度
140度x( )≠360度
144度x( )≠360度
根据:一种多边形能否密铺关键看它拼接点处的几个内角是否能组成360度。
巩固练习
2
下面两幅图形可以看作密铺吗?为什么?
两幅图形都不可以看作密铺,因为一种或几种平面图形形成拼接,彼此之间不留空隙、不重叠的铺成一片,才是平面图形的密铺。
(2)基本的平面图形能否单独密铺与图形的( )有关。
(3)四边形的内角和是( ),四边形能单独密铺。
填一填。
(1)一种或几种平面图形形成拼接,彼此之间不留空隙、不重叠的铺成一片,叫做平面图形的( )。
密铺
角度
360°
3
(1)下面的图形没有密铺的是( )。
B. C.
(2)当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个( )时,能密铺成一个平面图形。
A.直角 B.周角 C.平角
4
选一选。
B
B
交流反思
.看一看下面的密铺图案,想一想它们是如何形成的。
留心观察,你就能发现有很多密铺现象。
5
正方形
正六边形
戴帽子的美女头像
骑士
密铺的含义:
今天的收获:
哪些图形可以密铺: 三角形、四边形和正六边形都可以单独密铺。
一种多边形能否密铺关键看它的内角是否能组成360度。
课堂小结
把形状、大小相同的一种或几种平面图形不留空隙、不重叠的拼接在一起,这就是密铺。
自然艺术家
请你欣赏
阿罕伯拉宫
美妙的密铺世界
--荷兰艺术家埃舍尔作品欣赏
美妙的密铺世界
--荷兰艺术家埃舍尔作品欣赏
密铺或镶嵌艺术离我们很遥远吗?
学以致用
你能利用密铺的知识设计一幅地砖图案吗 试试看吧!
1.从课后习题中选取;
2.完成练习册本课时的习题。
3.预习课本79-80页。
4.利用密铺的知识设计一幅地砖图案。
课后作业
自我评价
在这次活动中,我的表现是(请把每项后面的☆涂上颜色,涂满5个为做得最好的):
同学们再见
数学好玩
北师大版 四年级下册
1.通过观察、操作,理解图形密铺的特征,了解三角形和四边形具有密铺特点。
2.通过猜想、操作等活动发展空间想象能力和动手能力,培养创新意识。
3.通过欣赏、设计和展示交流活动,进一步感受图形密铺的奇妙,感受数学的美,体验参与数学学习活动的乐趣。
【重点】理解什么是图形密铺。
【难点】探索三角形和四边形是否可以密铺。
学习目标:
课前准备:三角形、梯形、一般四边形、正五边形、正六边形的卡片若干张。
俄罗斯方块
G D
OO
课前导入:
密铺
在装修时经常要在地面或墙面上铺砖,
下面是瓷砖常见的铺法。
这些图形是怎样拼在一起的?什么是密铺
请观察,这些图形在拼接时有什么特点
不留空隙、不重叠
请观察,这些图形在拼接时有什么特点
不留空隙、不重叠
什么是密铺:
(1)用一种或几种全等图形进行拼接。
(2)拼接处不留空隙、不重叠。
(3)能连续铺成一片。
平面图形密铺的特点:
把形状、大小相同的一种或几种平面图形不留空隙、不重叠的拼接在一起,这就是密铺。
活动任务
三角形能不能密铺?四边形可不可以?
设计方案:
1.设计实验的步骤。
(1)准备大小,形状完全相同的三角形、梯形和一般四边形的卡片若干张。
(2)一人负责用三角形拼摆,一人负责用梯形拼摆,一人负责用一般四边形拼摆。
(3)观察是否密铺。
解决这个问题需要哪些主要步骤?
1.将准备好的三角形、梯形和一般四边形拼一拼,摆一摆。
2.收集实验结果并记录。
形状 三角形 梯形 一般四边形
是否密铺
动手实验
动手实验
1.按照设计方案将剪好的三角形拼一拼,
摆一摆。
发现:三角形可以密铺。
动手实验
1.按照设计方案将剪好的梯形拼一拼,
摆一摆。
发现:梯形可以密铺。
动手实验
1.按照设计方案将剪好的一般四边形拼一拼,
摆一摆。
发现:一般四边形可以密铺。
收集实验结果并记录。
形状 三角形 梯形 一般四边形
是否密铺
是
是
是
三角形和四边形都可以密铺
为什么可以呢
交流反思
1.请按照下面的方法试一试,你有什么发现?
我将相同图形的角按序号标好,密铺后发现……
三角形
梯形
一般四边形
结论:任意全等的三角形能密铺
三角形的每个内角在每个拼接点处出现两次,所以180°×2=360°
单独一种多边形密铺
周角
用形状、大小完全相同的任意四边形能否密铺?
四边形的每个内角在每个拼接点处出现一次,共:360°。
结论:任意全等的四边形能密铺
周角
2.在上面的活动中,你有什么收获?
密铺与图形的 角有关系。
密铺的图形中,拼接点处几个角的度数之和正好是360°
交流反思
3.不是所有的平面图形都可以密铺。看一看,试一
试。
正五边形
正六边形
啊!拼不了啦,为什么呢 你能说说原因吗
1
2
3
正五边形可以密铺吗?
108度
×( ?)
≠360度
108度
正五边形不可以密铺
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
120度
×3
=360度
120度
正六边形可以密铺
归纳小结:
三角形一定可以密铺.
正六边形可以密铺.
1.因为三角形的内角和是180°, 用几个全等三角形拼接时,每个角只需用两次,就能拼出一个周角,所以
2.任意四边形的四个内角之和是360°,而密铺时拼接点的四个角刚好能拼成一个周角,所以
任意四边形一定可以密铺.
3.正六边形的每个内角都是120°,也能拼接出周角,所以
结论:密铺与图形的角有关系,每个拼接点处,当几个多边形的内角和能组成360度时,则可以密铺,否则将无法进行密铺的。
(×)
(√)
(√)
(√)
(√)
(×)
三角形、四边形、正六边形可以进行单独密铺 。
圆形和正五边形不能进行单独密铺。
汇报:
1
当拼接点处的几个角的度数和为360°时,就能密铺。
单独一种多边形密铺
用同一种平面图形如果不能密铺, 用两种或者两种以上平面图形能不能密铺呢
两种多边形密铺探索
能
用同一种平面图形如果不能密铺, 用两种或者两种以上平面图形能不能密铺呢
能
这是密铺作品,这也是镶嵌,它是怎么样做出来的呢?
请往下看,实际上是很简单的
不规则图形密铺探索
你看懂了吗?实际上是用正方形“剪”“拼”出来的
用你掌握的知识来判断下面正多边形能否密铺.
正八边形(一个内角是135度)
正九边形(一个内角是140度)
正十边形(一个内角是144度)
不能密铺
不能密铺
不能密铺
1
135度x( )≠360度
140度x( )≠360度
144度x( )≠360度
根据:一种多边形能否密铺关键看它拼接点处的几个内角是否能组成360度。
巩固练习
2
下面两幅图形可以看作密铺吗?为什么?
两幅图形都不可以看作密铺,因为一种或几种平面图形形成拼接,彼此之间不留空隙、不重叠的铺成一片,才是平面图形的密铺。
(2)基本的平面图形能否单独密铺与图形的( )有关。
(3)四边形的内角和是( ),四边形能单独密铺。
填一填。
(1)一种或几种平面图形形成拼接,彼此之间不留空隙、不重叠的铺成一片,叫做平面图形的( )。
密铺
角度
360°
3
(1)下面的图形没有密铺的是( )。
B. C.
(2)当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个( )时,能密铺成一个平面图形。
A.直角 B.周角 C.平角
4
选一选。
B
B
交流反思
.看一看下面的密铺图案,想一想它们是如何形成的。
留心观察,你就能发现有很多密铺现象。
5
正方形
正六边形
戴帽子的美女头像
骑士
密铺的含义:
今天的收获:
哪些图形可以密铺: 三角形、四边形和正六边形都可以单独密铺。
一种多边形能否密铺关键看它的内角是否能组成360度。
课堂小结
把形状、大小相同的一种或几种平面图形不留空隙、不重叠的拼接在一起,这就是密铺。
自然艺术家
请你欣赏
阿罕伯拉宫
美妙的密铺世界
--荷兰艺术家埃舍尔作品欣赏
美妙的密铺世界
--荷兰艺术家埃舍尔作品欣赏
密铺或镶嵌艺术离我们很遥远吗?
学以致用
你能利用密铺的知识设计一幅地砖图案吗 试试看吧!
1.从课后习题中选取;
2.完成练习册本课时的习题。
3.预习课本79-80页。
4.利用密铺的知识设计一幅地砖图案。
课后作业
自我评价
在这次活动中,我的表现是(请把每项后面的☆涂上颜色,涂满5个为做得最好的):
同学们再见
