2022-2023学年华东师大版八年级数学上册 12.1.1 同底数幂的乘法 课件(共28张)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学上册 12.1.1 同底数幂的乘法 课件(共28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 19:32:11 | ||
图片预览







文档简介
(共28张PPT)
12.1.1同底数幂的乘法
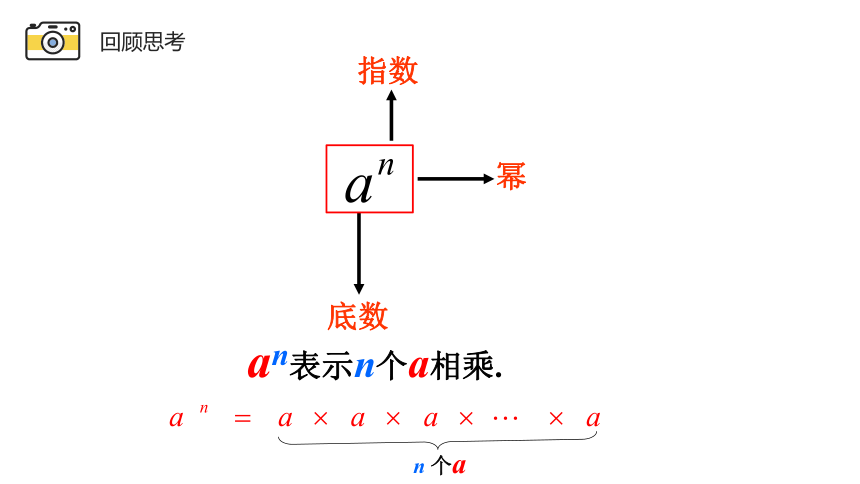
回顾思考
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
n个
3
5
n
①什么叫乘方
②乘方的结果叫做什么
求几个相同因数的积的运算叫做乘方。
3、a · a · · · · · · a = a( )
回顾思考
底数
幂
指数
an表示n个a相乘.
n 个a
回顾思考
将下列幂写成乘法形式:
(1) 108
(2) (-2)4
=10×10×10×10×10×10×10×10
=(-2)×(-2)×(-2)×(-2)
探究新知
光的速度为 3×105千米/秒,太阳光照射到地球上大约需要 5×102秒,地球距太阳大约多远?
解析:根据“路程=速度×时间”可得
地球距太阳(3×105)×(5×102)千米.
如何计算105×102呢?
探究新知
105×102
= (10×10×10×10×10)×(10×10)
计算:105×102
解析:根据乘方的意义,可得
5个10
2个10
= 10×10×10×10×10×10×10
(5+2)个10
= 105+2
即:105×102=105+2
探究新知
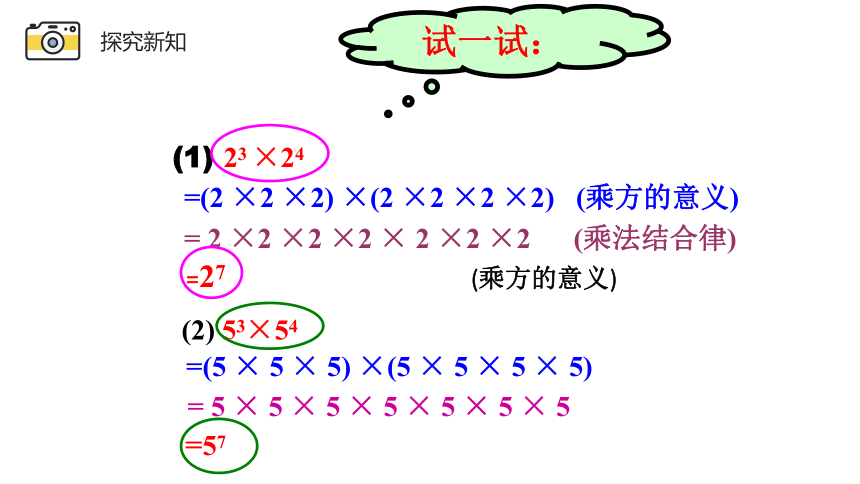
试一试:
=27 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
(1) 23 ×24
(2) 53×54
=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)
=57
探究新知
=a7 (乘方的意义)
继续探索:
(3) a3 · a4
=(a · a · a) (a · a · a · a) (乘方的意义)
= a · a · a · a · a · a · a (乘法结合律)
思考:观察上面各题上下两个圆圈里的式子,底数、指数有什么关系?
(3)a3 · a4
思考
(1)23 ×24
=a7
=27
(2)53×54
=57
思考:观察上面各题上下两个圆圈里的式子,底数、指数有什么关系?
(3)a3 · a4
思考
(1)23 ×24
=a7
=27
(2)53×54
=57
如果把(3)中指数3、4换成正整数m、n,你能得出am · an的结果吗?
(4)am · an =
(m、n都是正整数)
猜想
猜想: am · an= (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法法则:
猜想
结果:①底数不变 ②指数相加
条件:①乘法 ②底数相同
即:
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法法则:
小试牛刀
(1) 103×104 (2) a · a3
例1、计算
解:原式 =103+4
=107.
解:原式 = a1+3
= a4.
思考
am · an = am+n (m、n都是正整数)
同底数幂的乘法法则:
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
am·an·ap =
am+n+p
(m、n、p都是正整数)
小试牛刀
(1) a ·a3 ·a5
例2、计算
解:原式 = a1+3+5
= a9
思考
am · an = am+n (m、n都是正整数)
同底数幂的乘法法则:
想一想: 反之成立吗?
am+n =
am · an
(m、n都是正整数)
小试牛刀
例3、已知am=9,an=81,求am+n的值.
解:am+n =am·an
=9×81
=729.
底数互为相反数,偶次方相等,奇次方相反
底数互为相反数,偶次方相等,奇次方相反
小试牛刀
例4、计算
(1) (-b)3 ·b3 (2) (y-x)2 ·(x-y)3
解:原式=-b3·b3
=-b3+3
=-b6
解:原式
小结
一、同底数幂的乘法法则
二、同底数幂的乘法法则的拓展延伸
四、 与
三、同底数幂的逆运算
小试牛刀
① a · a2= a2
② a+a2 = a3
③ a3 · a3= a9
④ a3+a3 = a6
(×)
(×)
(×)
1.判断下列计算是否正确,并简要说明理由:
(×)
小试牛刀
2.填空
(1)x5 ·( )= x 8 (2)a ·( )= a6
(3)x · x3( )= x7 (4)xm ·( )=x3m
x3
a5
x3
x2m
小试牛刀
3.计算
小试牛刀
3.计算
小试牛刀
4.已知am= 8,an= 32,求am+n的值.
小试牛刀
5.已知3m= 6,3n+m= 48,求3n的值.
下课!
12.1.1同底数幂的乘法
回顾思考
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
n个
3
5
n
①什么叫乘方
②乘方的结果叫做什么
求几个相同因数的积的运算叫做乘方。
3、a · a · · · · · · a = a( )
回顾思考
底数
幂
指数
an表示n个a相乘.
n 个a
回顾思考
将下列幂写成乘法形式:
(1) 108
(2) (-2)4
=10×10×10×10×10×10×10×10
=(-2)×(-2)×(-2)×(-2)
探究新知
光的速度为 3×105千米/秒,太阳光照射到地球上大约需要 5×102秒,地球距太阳大约多远?
解析:根据“路程=速度×时间”可得
地球距太阳(3×105)×(5×102)千米.
如何计算105×102呢?
探究新知
105×102
= (10×10×10×10×10)×(10×10)
计算:105×102
解析:根据乘方的意义,可得
5个10
2个10
= 10×10×10×10×10×10×10
(5+2)个10
= 105+2
即:105×102=105+2
探究新知
试一试:
=27 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
(1) 23 ×24
(2) 53×54
=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)
=57
探究新知
=a7 (乘方的意义)
继续探索:
(3) a3 · a4
=(a · a · a) (a · a · a · a) (乘方的意义)
= a · a · a · a · a · a · a (乘法结合律)
思考:观察上面各题上下两个圆圈里的式子,底数、指数有什么关系?
(3)a3 · a4
思考
(1)23 ×24
=a7
=27
(2)53×54
=57
思考:观察上面各题上下两个圆圈里的式子,底数、指数有什么关系?
(3)a3 · a4
思考
(1)23 ×24
=a7
=27
(2)53×54
=57
如果把(3)中指数3、4换成正整数m、n,你能得出am · an的结果吗?
(4)am · an =
(m、n都是正整数)
猜想
猜想: am · an= (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法法则:
猜想
结果:①底数不变 ②指数相加
条件:①乘法 ②底数相同
即:
am · an = am+n (m、n都是正整数)
同底数幂相乘,
底数 ,指数 。
不变
相加
同底数幂的乘法法则:
小试牛刀
(1) 103×104 (2) a · a3
例1、计算
解:原式 =103+4
=107.
解:原式 = a1+3
= a4.
思考
am · an = am+n (m、n都是正整数)
同底数幂的乘法法则:
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
am·an·ap =
am+n+p
(m、n、p都是正整数)
小试牛刀
(1) a ·a3 ·a5
例2、计算
解:原式 = a1+3+5
= a9
思考
am · an = am+n (m、n都是正整数)
同底数幂的乘法法则:
想一想: 反之成立吗?
am+n =
am · an
(m、n都是正整数)
小试牛刀
例3、已知am=9,an=81,求am+n的值.
解:am+n =am·an
=9×81
=729.
底数互为相反数,偶次方相等,奇次方相反
底数互为相反数,偶次方相等,奇次方相反
小试牛刀
例4、计算
(1) (-b)3 ·b3 (2) (y-x)2 ·(x-y)3
解:原式=-b3·b3
=-b3+3
=-b6
解:原式
小结
一、同底数幂的乘法法则
二、同底数幂的乘法法则的拓展延伸
四、 与
三、同底数幂的逆运算
小试牛刀
① a · a2= a2
② a+a2 = a3
③ a3 · a3= a9
④ a3+a3 = a6
(×)
(×)
(×)
1.判断下列计算是否正确,并简要说明理由:
(×)
小试牛刀
2.填空
(1)x5 ·( )= x 8 (2)a ·( )= a6
(3)x · x3( )= x7 (4)xm ·( )=x3m
x3
a5
x3
x2m
小试牛刀
3.计算
小试牛刀
3.计算
小试牛刀
4.已知am= 8,an= 32,求am+n的值.
小试牛刀
5.已知3m= 6,3n+m= 48,求3n的值.
下课!
