人教版七年级上册 3.1.1从算式到方程 课件(共32张PPT)
文档属性
| 名称 | 人教版七年级上册 3.1.1从算式到方程 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 20:09:11 | ||
图片预览








文档简介
(共32张PPT)
创设情境,回顾概念
1.“猜一猜我的年龄”
我是11月出生的,我年龄的2倍加上6,正好是我出生的那个月总天数的2倍,请你们猜一猜我的年龄是多少岁?
你能举出一些方程的例子吗?
含有未知数的等式——方程
创设情境,回顾概念
2.“日历中的数学”
游戏:请同学们圈出日历中一个竖列上相邻的三个日期,把它们的和告诉老师,老师能马上知道这三天分别是几号.请同学们想想老师是如何得到答案的.
3.1 从算式到方程
第三章 一元一次方程
3.1.1 一元一次方程
学习目标
1.了解方程、一元一次方程、方程的解和解方程的相关概念,且能识别一元一次方程.(重点)
2.会判断一个数是否为方程的解.(重点)
3.能根据问题设未知数,并列出方程.(重点、难点)
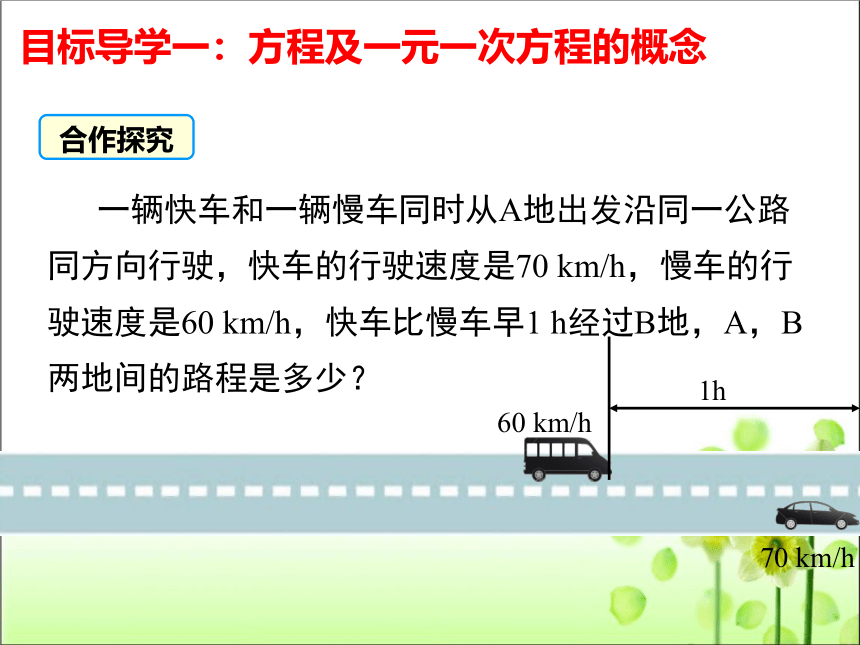
一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70 km/h,慢车的行驶速度是60 km/h,快车比慢车早1 h经过B地,A,B两地间的路程是多少?
合作探究
1h
60 km/h
70 km/h
目标导学一:方程及一元一次方程的概念
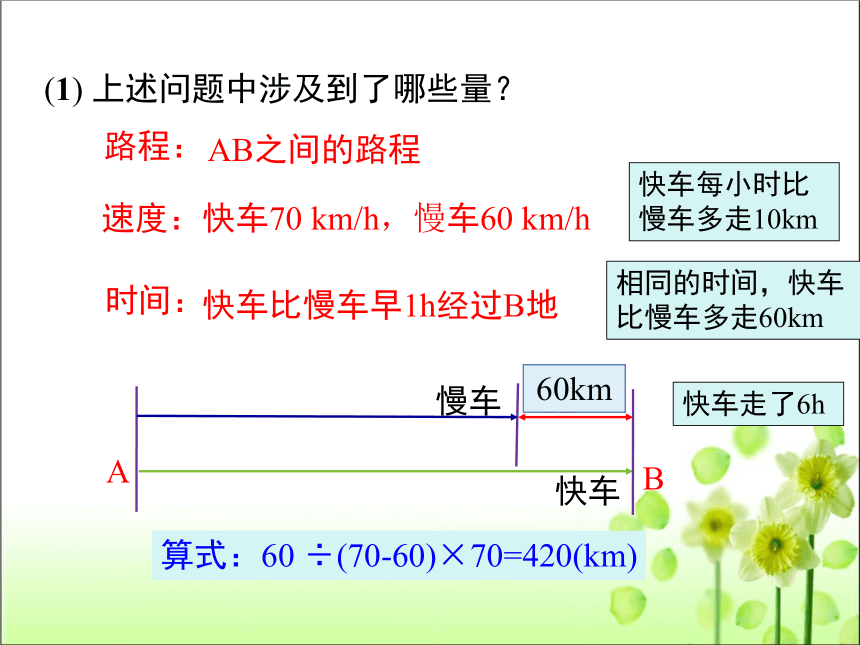
(1) 上述问题中涉及到了哪些量?
快车70 km/h,慢车60 km/h
快车比慢车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km
60km
相同的时间,快车比慢车多走60km
快车走了6h
算式:60 ÷(70-60)×70=420(km)
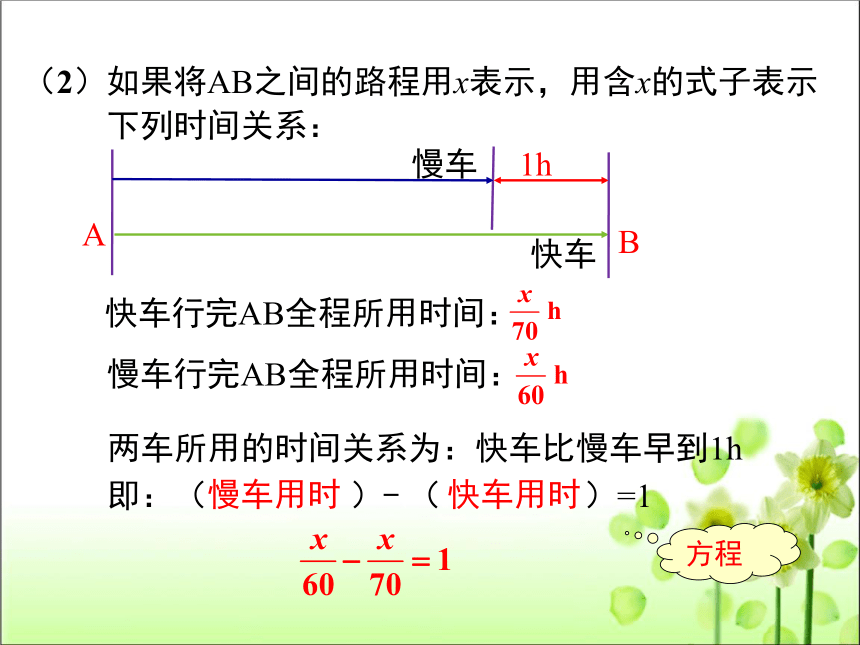
(2)如果将AB之间的路程用x表示,用含x的式子表示
下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:( )- ( )=1
慢车用时
快车用时
方程
A
B
快车
慢车
1h
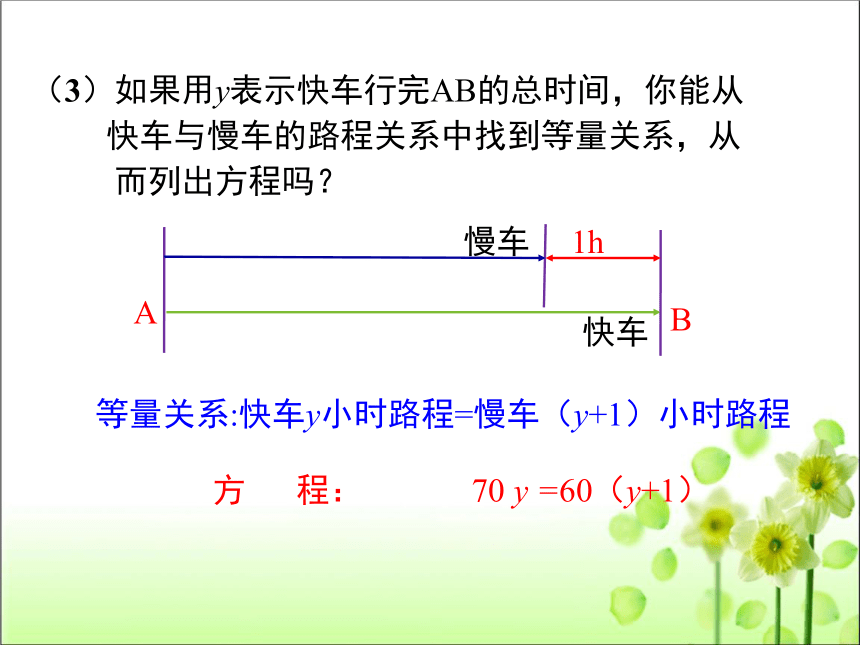
(3)如果用y表示快车行完AB的总时间,你能从
快车与慢车的路程关系中找到等量关系,从
而列出方程吗?
方 程: 70 y =60(y+1)
等量关系:快车y小时路程=慢车(y+1)小时路程
A
B
快车
慢车
1h
上面我们列出的方程有什么特点?
它们都只含有一个未知数,并且未知数的次数都是1
只含有一个未知数,并且未知数的次数是1的方程。
一元一次方程:
温馨提示:
1、含有未知量的个数
2、未知量的次数 两方面考虑。
【总结提升】
判断一元一次方程的三个条件
(1)必须只含有一个未知数.
(2)未知数的次数都是1.
(3)等号两边都是整式.
判断下列各式哪些是方程?
我回顾,我思考
①5x+3y-6x=37( ) ②4x-7( )
③5x ≥ 3 ( ) ④ 6x +x-2=0 ( )
⑤1+2=3 ( ) ⑥ ( )
×
√
×
×
√
√
练习二:下列式子哪些是方程,哪些是一元一次方程?
①9x=2 ②x+2y=0
③x2-1=0 ④x=0
⑤ ⑥3a+9
小试身手
① ② ③ ④ ⑤是方程;
① ④是一元一次方程。
列方程时,要先设字母表示未知数,然后根据问题中的等量关系,写出含有未知数的等式——方程。
问题 怎么列方程呢?
定义方程,感受过程
根据下列问题,设未
知数并列出方程:
例1.一台计算机已使用1 700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的修检时间2 450小时?
解:
设x月后这台计算机的使用时间达到2 450小时,
那么在x月后使用了(1 700+150x)小时.
列方程得:
1 700+150x=2 450.
目标导学二:列方程
例2. 用一根长24cm的铁丝围成一个长方形,使它长是宽的1.5倍,长方形的长、宽各应是多少
解:
设长方形的宽为 x cm,那么长为1.5x cm.
列方程得:
2(x+1.5x)=24.
x
1.5x
例3.某校女生占全体学生的52%,比男生 多80人,这个学校有多少学生?
解:
设这个学校的学生有x人,那么女生数为0.52x,男生数为(1-0.52)x.
列方程得:
0.52x-(1-0.52)x=80.
小结:
实际问题
一元一次方程
设未知数
找等量关系
1.设:恰当的设出未知数,用字母X表示问题中的未知量
3.列:利用实际问题中的相等关系列出方程
2.找:寻找实际问题中的相等关系
关键
列出一元一次方程的一般步骤:
例4.甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
解:设甲种铅笔买了x支,乙种铅笔买了(20-x)支,
0.3x+0.6(20-x)= 9
一个梯形的下底比上底多2 cm,高是5 cm,
面积是40 cm2,求上底.
解:设上底为x cm,
(x+x+2)×5 = 40
练一练
对于方程4x=24,容易知道 x = 6可以使等式成立, 对于方程 170+15x =245,你知道 x 等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程 170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
思
考
目标导学三:方程的解
使方程左右两边相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是 方程的解吗
知识要点
方程的解
例5 若关于x的方程 是一元一次方程,则
n 的值为 .
【变式题】加了限制条件,需进行取舍.
方程 是关于x的一元一次方程,则m= .
2或-2
1
注:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
例6 检验 x=3是不是方程 2x-3=5x-15的解.
解:把 x=3分别代入方程的左边和右边,得
左边=2×3-3=3,
右边=5×3-15=0.
∵左边≠右边,
∴ x=3不是方程的解.
判断方程解的三个步骤
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.
1. 一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两
边都是整式,这样的方程叫做一元一次方程.
2. 方程的解:
解方程就是求出使方程中等号两边相等的未知
数的值,这个值就是方程的解.
1.下列方程为一元一次方程的是( )
A.x+5=y+4 B.
C.x2-x=1 D.x=0
检测目标
D
2.“五一”期间,某电器按成本价提高30%后标价,再打8折(标价的80%)销售,售价为2 080元.设该电器的成本价为x元,根据题意,下面所列方程正确的是( )
A.x(1+30%)×80%=2 080 B.x·30%·80%=2 080
C.2 080×30%×80%=x D.x·30%=2 080×80%
检测目标
A
3.已知下列方程:①x-2= ②0.3x=1;③
④x2-4x=3;⑤x=0;⑥x+2y=0,其中是一元一次方程的有( )
A.2个 B.3个 C.4个 D.5个
检测目标
B
4.甲乙两数的和为10,并且甲比乙大2,求甲、乙两数.下面所列方程正确的是( )
A.设乙数为x,则x+2=10
B.设乙数为x,则(x-2)+x=10
C.设甲数为x,则(x+2)+x=10
D.设乙数为x,则(x+2)+x=10
检测目标
D
5.下列方程中,解为x=3的是( )
A.6x=2 B.3x-9=0
C. D.5x+15=0
检测目标
B
谈谈你的收获吧
谢谢大家的努力
创设情境,回顾概念
1.“猜一猜我的年龄”
我是11月出生的,我年龄的2倍加上6,正好是我出生的那个月总天数的2倍,请你们猜一猜我的年龄是多少岁?
你能举出一些方程的例子吗?
含有未知数的等式——方程
创设情境,回顾概念
2.“日历中的数学”
游戏:请同学们圈出日历中一个竖列上相邻的三个日期,把它们的和告诉老师,老师能马上知道这三天分别是几号.请同学们想想老师是如何得到答案的.
3.1 从算式到方程
第三章 一元一次方程
3.1.1 一元一次方程
学习目标
1.了解方程、一元一次方程、方程的解和解方程的相关概念,且能识别一元一次方程.(重点)
2.会判断一个数是否为方程的解.(重点)
3.能根据问题设未知数,并列出方程.(重点、难点)
一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70 km/h,慢车的行驶速度是60 km/h,快车比慢车早1 h经过B地,A,B两地间的路程是多少?
合作探究
1h
60 km/h
70 km/h
目标导学一:方程及一元一次方程的概念
(1) 上述问题中涉及到了哪些量?
快车70 km/h,慢车60 km/h
快车比慢车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km
60km
相同的时间,快车比慢车多走60km
快车走了6h
算式:60 ÷(70-60)×70=420(km)
(2)如果将AB之间的路程用x表示,用含x的式子表示
下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:( )- ( )=1
慢车用时
快车用时
方程
A
B
快车
慢车
1h
(3)如果用y表示快车行完AB的总时间,你能从
快车与慢车的路程关系中找到等量关系,从
而列出方程吗?
方 程: 70 y =60(y+1)
等量关系:快车y小时路程=慢车(y+1)小时路程
A
B
快车
慢车
1h
上面我们列出的方程有什么特点?
它们都只含有一个未知数,并且未知数的次数都是1
只含有一个未知数,并且未知数的次数是1的方程。
一元一次方程:
温馨提示:
1、含有未知量的个数
2、未知量的次数 两方面考虑。
【总结提升】
判断一元一次方程的三个条件
(1)必须只含有一个未知数.
(2)未知数的次数都是1.
(3)等号两边都是整式.
判断下列各式哪些是方程?
我回顾,我思考
①5x+3y-6x=37( ) ②4x-7( )
③5x ≥ 3 ( ) ④ 6x +x-2=0 ( )
⑤1+2=3 ( ) ⑥ ( )
×
√
×
×
√
√
练习二:下列式子哪些是方程,哪些是一元一次方程?
①9x=2 ②x+2y=0
③x2-1=0 ④x=0
⑤ ⑥3a+9
小试身手
① ② ③ ④ ⑤是方程;
① ④是一元一次方程。
列方程时,要先设字母表示未知数,然后根据问题中的等量关系,写出含有未知数的等式——方程。
问题 怎么列方程呢?
定义方程,感受过程
根据下列问题,设未
知数并列出方程:
例1.一台计算机已使用1 700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的修检时间2 450小时?
解:
设x月后这台计算机的使用时间达到2 450小时,
那么在x月后使用了(1 700+150x)小时.
列方程得:
1 700+150x=2 450.
目标导学二:列方程
例2. 用一根长24cm的铁丝围成一个长方形,使它长是宽的1.5倍,长方形的长、宽各应是多少
解:
设长方形的宽为 x cm,那么长为1.5x cm.
列方程得:
2(x+1.5x)=24.
x
1.5x
例3.某校女生占全体学生的52%,比男生 多80人,这个学校有多少学生?
解:
设这个学校的学生有x人,那么女生数为0.52x,男生数为(1-0.52)x.
列方程得:
0.52x-(1-0.52)x=80.
小结:
实际问题
一元一次方程
设未知数
找等量关系
1.设:恰当的设出未知数,用字母X表示问题中的未知量
3.列:利用实际问题中的相等关系列出方程
2.找:寻找实际问题中的相等关系
关键
列出一元一次方程的一般步骤:
例4.甲种铅笔每支0.3 元,乙种铅笔每支0.6 元,用9 元钱买了两种铅笔共20 支,两种铅笔各买了多少支?
解:设甲种铅笔买了x支,乙种铅笔买了(20-x)支,
0.3x+0.6(20-x)= 9
一个梯形的下底比上底多2 cm,高是5 cm,
面积是40 cm2,求上底.
解:设上底为x cm,
(x+x+2)×5 = 40
练一练
对于方程4x=24,容易知道 x = 6可以使等式成立, 对于方程 170+15x =245,你知道 x 等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程 170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
思
考
目标导学三:方程的解
使方程左右两边相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是 方程的解吗
知识要点
方程的解
例5 若关于x的方程 是一元一次方程,则
n 的值为 .
【变式题】加了限制条件,需进行取舍.
方程 是关于x的一元一次方程,则m= .
2或-2
1
注:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
例6 检验 x=3是不是方程 2x-3=5x-15的解.
解:把 x=3分别代入方程的左边和右边,得
左边=2×3-3=3,
右边=5×3-15=0.
∵左边≠右边,
∴ x=3不是方程的解.
判断方程解的三个步骤
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.
1. 一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两
边都是整式,这样的方程叫做一元一次方程.
2. 方程的解:
解方程就是求出使方程中等号两边相等的未知
数的值,这个值就是方程的解.
1.下列方程为一元一次方程的是( )
A.x+5=y+4 B.
C.x2-x=1 D.x=0
检测目标
D
2.“五一”期间,某电器按成本价提高30%后标价,再打8折(标价的80%)销售,售价为2 080元.设该电器的成本价为x元,根据题意,下面所列方程正确的是( )
A.x(1+30%)×80%=2 080 B.x·30%·80%=2 080
C.2 080×30%×80%=x D.x·30%=2 080×80%
检测目标
A
3.已知下列方程:①x-2= ②0.3x=1;③
④x2-4x=3;⑤x=0;⑥x+2y=0,其中是一元一次方程的有( )
A.2个 B.3个 C.4个 D.5个
检测目标
B
4.甲乙两数的和为10,并且甲比乙大2,求甲、乙两数.下面所列方程正确的是( )
A.设乙数为x,则x+2=10
B.设乙数为x,则(x-2)+x=10
C.设甲数为x,则(x+2)+x=10
D.设乙数为x,则(x+2)+x=10
检测目标
D
5.下列方程中,解为x=3的是( )
A.6x=2 B.3x-9=0
C. D.5x+15=0
检测目标
B
谈谈你的收获吧
谢谢大家的努力
