2022-2023学年人教版八年级数学上册12.2.3“角边角”“角角边”课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2.3“角边角”“角角边”课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 23:11:59 | ||
图片预览

文档简介
(共15张PPT)
12.2 三角形全等的判定
第十二章 全等三角形
八年级数学上(RJ)
教学课件
第3课时 “角边角”“角角边”
八年级数学上(RJ)
教学课件
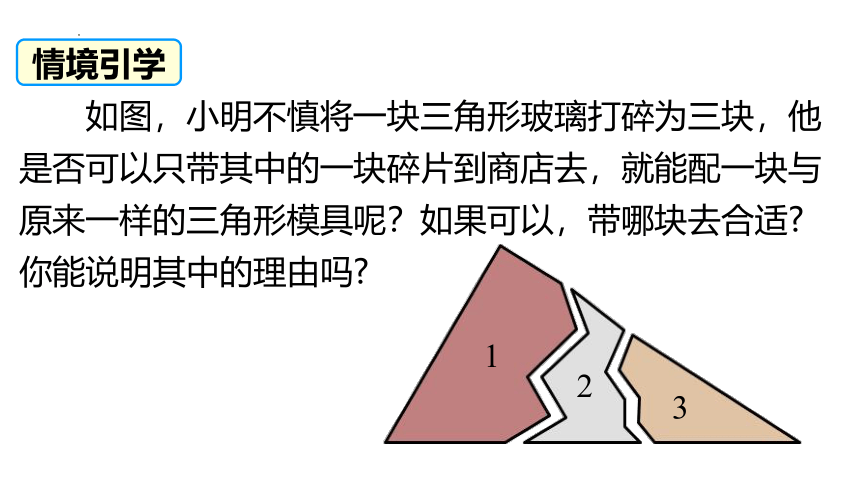
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适
你能说明其中的理由吗
情境引学
3
2
1
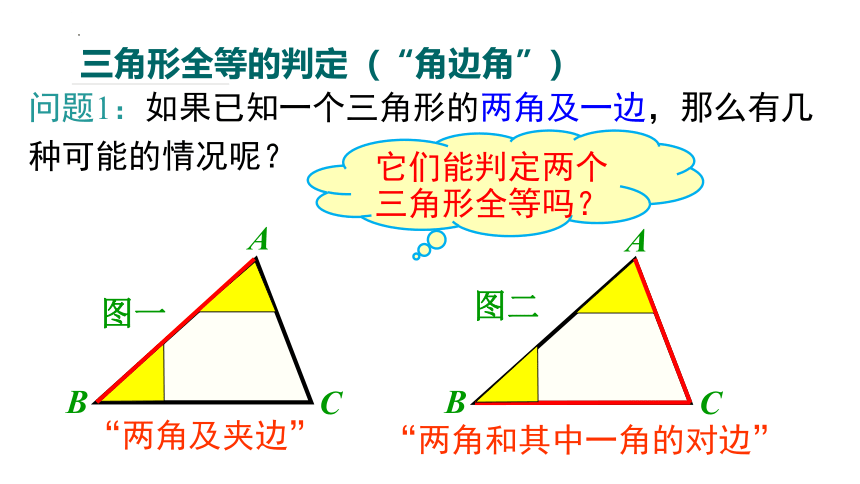
三角形全等的判定(“角边角”)
问题1:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
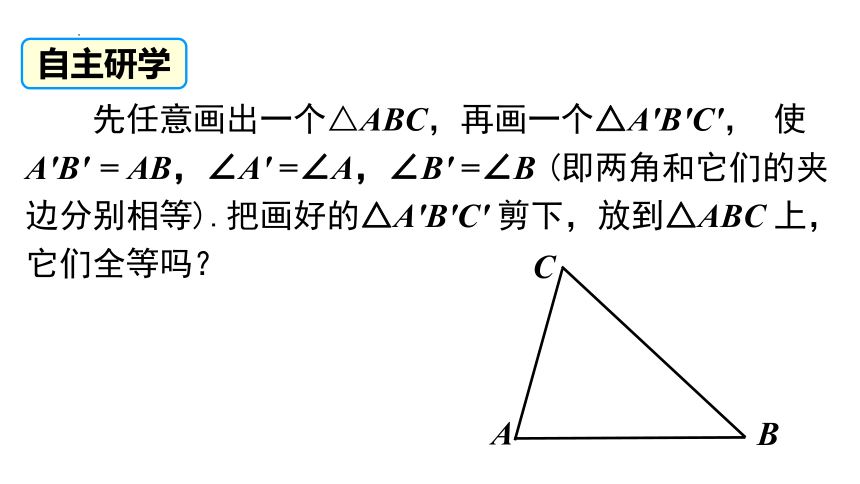
先任意画出一个△ABC,再画一个△A′B′C′, 使 A′B′ = AB,∠A′ =∠A,∠B′ =∠B (即两角和它们的夹边分别相等).把画好的△A′B′C′ 剪下,放到△ABC 上,它们全等吗?
自主研学
A
C
B
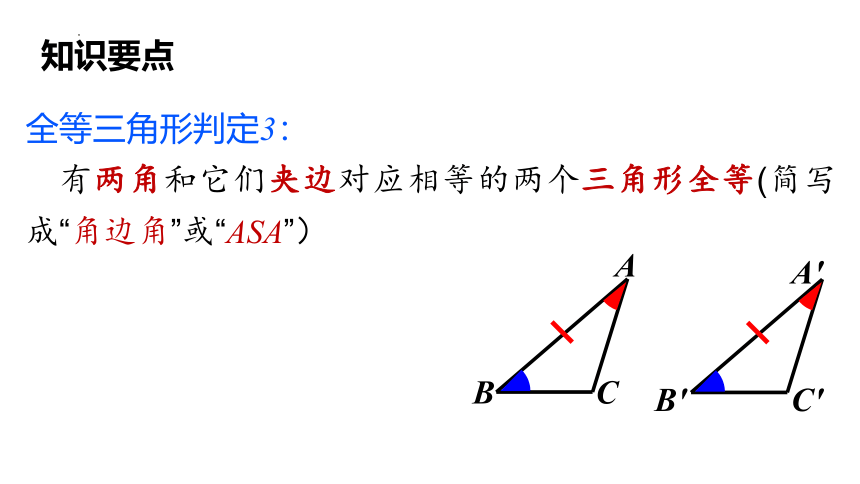
知识要点
全等三角形判定3:
有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)
A
B
C
A′
B′
C′
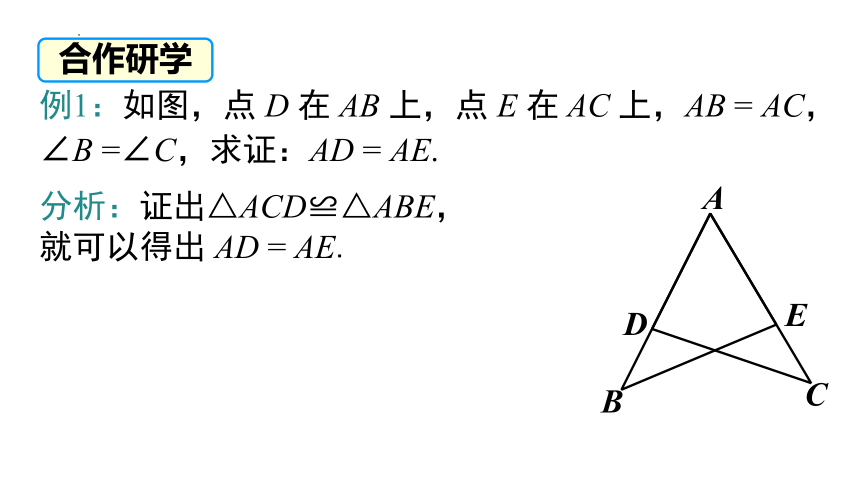
例1:如图,点 D 在 AB 上,点 E 在 AC 上,AB = AC, ∠B =∠C,求证:AD = AE.
分析:证出△ACD≌△ABE,就可以得出 AD = AE.
A
B
C
D
E
合作研学
例2: 在△ABC 和△DEF 中,∠A=∠D,∠B=∠E,BC = EF.
求证:△ABC≌△DEF.
变换拓学
全等三角形判定4:
两角和其中一角的对边对应相等的两个三角形全等
(简写成“角角边”或“AAS”)
归纳总结
A
B
C
A′
B′
C′
学以致用:如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
答:可以带 1 去,因为两角且夹边分别相等的两个三角形全等.
1、如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
(1)CE=DF, , (ASA)
(2)∠C=∠D, , (ASA)
(3)AC=BD, AC∥BD, (ASA)
(4)AC∥BD,CE=DF, (AAS)
当堂练习
2. 如图,已知∠ACB =∠DBC,∠ABC =∠CDB,判断下面的两个三角形是否全等,并说明理由.
答:不全等,因为 BC 虽然是公共边,但并不对应.
A
B
C
D
3.已知:∠ABC = ∠DCB,∠ACB = ∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB (已知),
BC=CB (公共边),
∠ACB=∠DBC (已知),
证明:
在△ABC 和△DCB 中,
∴△ABC≌△DCB (ASA ).
B
C
A
D
判定方法:两角和它们的夹边分别相等的两个三角形全等.
课堂小结
小结:这节课我们主要学习了哪些知识
作业:基础P41 练习 第1题
鼓励P44 习题 第4题
挑战P44 习题 第5题
谢谢大家的聆听!
12.2 三角形全等的判定
第十二章 全等三角形
八年级数学上(RJ)
教学课件
第3课时 “角边角”“角角边”
八年级数学上(RJ)
教学课件
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适
你能说明其中的理由吗
情境引学
3
2
1
三角形全等的判定(“角边角”)
问题1:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
先任意画出一个△ABC,再画一个△A′B′C′, 使 A′B′ = AB,∠A′ =∠A,∠B′ =∠B (即两角和它们的夹边分别相等).把画好的△A′B′C′ 剪下,放到△ABC 上,它们全等吗?
自主研学
A
C
B
知识要点
全等三角形判定3:
有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)
A
B
C
A′
B′
C′
例1:如图,点 D 在 AB 上,点 E 在 AC 上,AB = AC, ∠B =∠C,求证:AD = AE.
分析:证出△ACD≌△ABE,就可以得出 AD = AE.
A
B
C
D
E
合作研学
例2: 在△ABC 和△DEF 中,∠A=∠D,∠B=∠E,BC = EF.
求证:△ABC≌△DEF.
变换拓学
全等三角形判定4:
两角和其中一角的对边对应相等的两个三角形全等
(简写成“角角边”或“AAS”)
归纳总结
A
B
C
A′
B′
C′
学以致用:如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢 如果可以,带哪块去合适 你能说明其中理由吗
3
2
1
答:可以带 1 去,因为两角且夹边分别相等的两个三角形全等.
1、如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
(1)CE=DF, , (ASA)
(2)∠C=∠D, , (ASA)
(3)AC=BD, AC∥BD, (ASA)
(4)AC∥BD,CE=DF, (AAS)
当堂练习
2. 如图,已知∠ACB =∠DBC,∠ABC =∠CDB,判断下面的两个三角形是否全等,并说明理由.
答:不全等,因为 BC 虽然是公共边,但并不对应.
A
B
C
D
3.已知:∠ABC = ∠DCB,∠ACB = ∠DBC.
求证:△ABC≌△DCB.
∠ABC=∠DCB (已知),
BC=CB (公共边),
∠ACB=∠DBC (已知),
证明:
在△ABC 和△DCB 中,
∴△ABC≌△DCB (ASA ).
B
C
A
D
判定方法:两角和它们的夹边分别相等的两个三角形全等.
课堂小结
小结:这节课我们主要学习了哪些知识
作业:基础P41 练习 第1题
鼓励P44 习题 第4题
挑战P44 习题 第5题
谢谢大家的聆听!
