人教版九年级上册数学 22.3实际问题与二次函数同步练习(含答案)
文档属性
| 名称 | 人教版九年级上册数学 22.3实际问题与二次函数同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 307.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 06:50:02 | ||
图片预览

文档简介
人教版九年级上册数学22.3 实际问题与二次函数同步练习
一、单选题
1.一件商品的原价是100元,经过两次提价后的价格为y元,每次提价的百分率是x,则y与x的函数关系式是( )
A.y=100(1+2x) B.y=100(1﹣2x)
C.y=100(1+x) D.y=100(1﹣x)
2.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=﹣(x﹣2)2+6,则水柱的最大高度是( )
A.2 B.4 C.6 D.2+
3.某商品现在的售价为每件35元,每天可卖出50件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,求最大销售额是( )
A.2500元 B.2000元 C.1800元 D.2200元
4.如图,抛物线y=ax2+bx+c的顶点M在矩形ABCD区域内(含边界),且该抛物线经过原点O(0,0),则a的取值范围是( )
A.-2≤a≤-1 B. C. D.
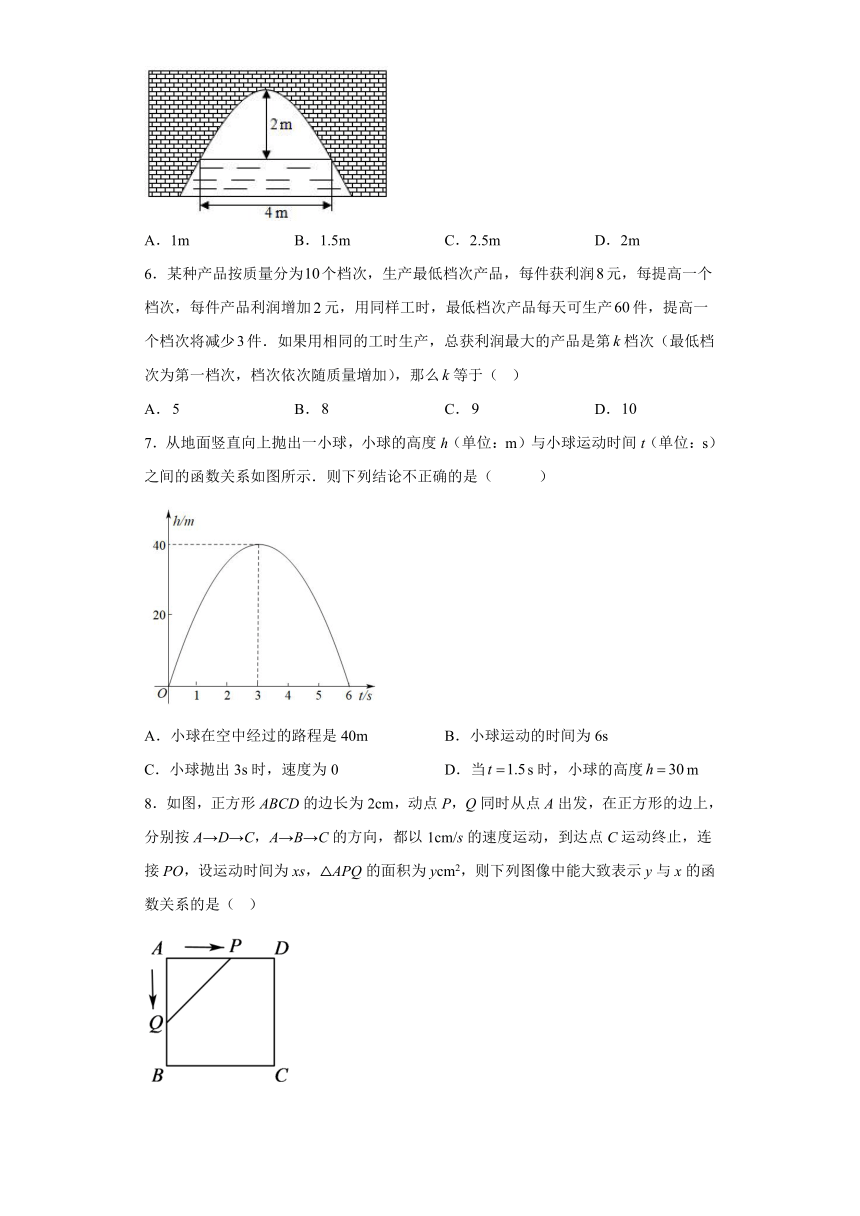
5.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
6.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
8.如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PO,设运动时间为xs,△APQ的面积为ycm2,则下列图像中能大致表示y与x的函数关系的是( )
A. B.C. D.
二、填空题
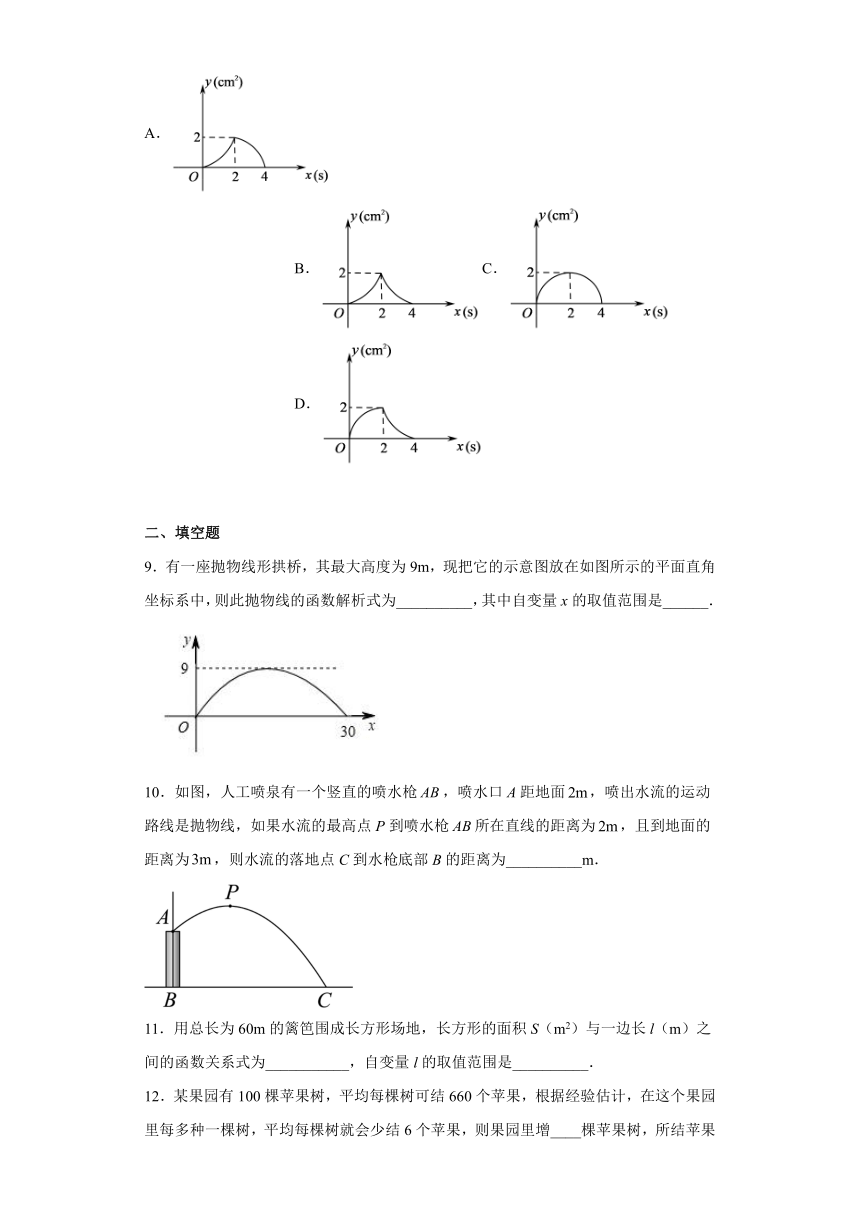
9.有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为__________,其中自变量x的取值范围是______.
10.如图,人工喷泉有一个竖直的喷水枪,喷水口A距地面,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪所在直线的距离为,且到地面的距离为,则水流的落地点C到水枪底部B的距离为__________m.
11.用总长为60m的篱笆围成长方形场地,长方形的面积S(m2)与一边长l(m)之间的函数关系式为___________,自变量l的取值范围是__________.
12.某果园有100棵苹果树,平均每棵树可结660个苹果,根据经验估计,在这个果园里每多种一棵树,平均每棵树就会少结6个苹果,则果园里增____棵苹果树,所结苹果的总数最多.
13.某商品的销售利润y与销售单价x的关系为y=+2650,则当x=___元时,y有最_______值,这个值为______元.
14.某大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为轴,建立如图所示的平面直角坐标系,水在空中画出的曲线是抛物线的一部分,则水喷出的水平距离最大为________米.
15.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是,该型号飞机着陆后滑行的最大距离是______.
16.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为 __;自变量x的取值范围为 __.
三、解答题
17.某商店销售一批头盔,售价为每顶60元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶40元,设每顶头盔的售价为x元,每月的销售量为y.
(1)直接写出y与x的函数关系式;
(2)若该商店每月获取2500元的利润,则每顶头盔的售价应定为多少?
(3)每顶头盔的售价为多少时,该商店每月可获取最大利润?最大利润为多少?
18.端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵10元,一盒猪肉粽加两盒豆沙粽进价为100元.
(1)求每盒猪肉粽和豆沙粽的进价;
(2)在销售中,某商家发现当每盒猪肉粽售价为50元时,每天可售出100盒,若每盒售价提高1元,则每天少售出2盒.设每盒猪肉粽售价为元,销售猪肉粽的利润为元,求该商家每天销售猪肉粽获得的最大利润.
19.如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为y.
(1)求y与x的函数关系式,(不必写出自变量x的取值范围)
(2)写出此二次函数的二次项系数、一次项系数和常数项;
(3)写出次函数的图像的对称轴及顶点坐标.
20.某乡镇贸易公司开设了一家网店,销售当地某种农产品,已知该农产品成本为每千克10元,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中10(1)写出y与x之间的函数关系式及自变量的取值范围;
(2)当销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
参考答案:
1.C
2.C
3.C
4.D
5.C
6.C
7.A
8.A
9.
10.
11. 0<l<30
12.5
13. 50 大 2650
14.4
15.600m
16.
17.(1)y=﹣20x+1400
(2)45元或65元
(3)每顶头盔的售价为55元时,该商店每月可获取最大利润,最大利润为4500元
18.(1)每盒猪肉粽的进价为40元,每盒豆沙粽进价为30元
(2)1800元
19.(1)y=-+15x(0<x≤18),
(2)二次项系数为,一次项系数为15,常数项为0
(3)对称轴x=15;及顶点坐标(15,)
20.(1)
(2)当销售单价x为28元时,每天的销售利润最大,最大利润是6480元
答案第2页,共2页
一、单选题
1.一件商品的原价是100元,经过两次提价后的价格为y元,每次提价的百分率是x,则y与x的函数关系式是( )
A.y=100(1+2x) B.y=100(1﹣2x)
C.y=100(1+x) D.y=100(1﹣x)
2.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=﹣(x﹣2)2+6,则水柱的最大高度是( )
A.2 B.4 C.6 D.2+
3.某商品现在的售价为每件35元,每天可卖出50件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,求最大销售额是( )
A.2500元 B.2000元 C.1800元 D.2200元
4.如图,抛物线y=ax2+bx+c的顶点M在矩形ABCD区域内(含边界),且该抛物线经过原点O(0,0),则a的取值范围是( )
A.-2≤a≤-1 B. C. D.
5.如图是抛物线形的拱桥,当水面宽4m时,顶点离水面2m,当水面宽度增加到6m时,水面下降( )
A.1m B.1.5m C.2.5m D.2m
6.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
8.如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PO,设运动时间为xs,△APQ的面积为ycm2,则下列图像中能大致表示y与x的函数关系的是( )
A. B.C. D.
二、填空题
9.有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为__________,其中自变量x的取值范围是______.
10.如图,人工喷泉有一个竖直的喷水枪,喷水口A距地面,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪所在直线的距离为,且到地面的距离为,则水流的落地点C到水枪底部B的距离为__________m.
11.用总长为60m的篱笆围成长方形场地,长方形的面积S(m2)与一边长l(m)之间的函数关系式为___________,自变量l的取值范围是__________.
12.某果园有100棵苹果树,平均每棵树可结660个苹果,根据经验估计,在这个果园里每多种一棵树,平均每棵树就会少结6个苹果,则果园里增____棵苹果树,所结苹果的总数最多.
13.某商品的销售利润y与销售单价x的关系为y=+2650,则当x=___元时,y有最_______值,这个值为______元.
14.某大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为轴,建立如图所示的平面直角坐标系,水在空中画出的曲线是抛物线的一部分,则水喷出的水平距离最大为________米.
15.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是,该型号飞机着陆后滑行的最大距离是______.
16.如图所示,用长为21米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃,为便于进出,开了3道宽为1米的门.设花圃的宽AB为x米,面积为S平方米,则S与x的之间的函数表达式为 __;自变量x的取值范围为 __.
三、解答题
17.某商店销售一批头盔,售价为每顶60元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶40元,设每顶头盔的售价为x元,每月的销售量为y.
(1)直接写出y与x的函数关系式;
(2)若该商店每月获取2500元的利润,则每顶头盔的售价应定为多少?
(3)每顶头盔的售价为多少时,该商店每月可获取最大利润?最大利润为多少?
18.端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵10元,一盒猪肉粽加两盒豆沙粽进价为100元.
(1)求每盒猪肉粽和豆沙粽的进价;
(2)在销售中,某商家发现当每盒猪肉粽售价为50元时,每天可售出100盒,若每盒售价提高1元,则每天少售出2盒.设每盒猪肉粽售价为元,销售猪肉粽的利润为元,求该商家每天销售猪肉粽获得的最大利润.
19.如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为y.
(1)求y与x的函数关系式,(不必写出自变量x的取值范围)
(2)写出此二次函数的二次项系数、一次项系数和常数项;
(3)写出次函数的图像的对称轴及顶点坐标.
20.某乡镇贸易公司开设了一家网店,销售当地某种农产品,已知该农产品成本为每千克10元,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中10
(2)当销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
参考答案:
1.C
2.C
3.C
4.D
5.C
6.C
7.A
8.A
9.
10.
11. 0<l<30
12.5
13. 50 大 2650
14.4
15.600m
16.
17.(1)y=﹣20x+1400
(2)45元或65元
(3)每顶头盔的售价为55元时,该商店每月可获取最大利润,最大利润为4500元
18.(1)每盒猪肉粽的进价为40元,每盒豆沙粽进价为30元
(2)1800元
19.(1)y=-+15x(0<x≤18),
(2)二次项系数为,一次项系数为15,常数项为0
(3)对称轴x=15;及顶点坐标(15,)
20.(1)
(2)当销售单价x为28元时,每天的销售利润最大,最大利润是6480元
答案第2页,共2页
同课章节目录
