北师大版2022--2023八年级(上)数学第四单元质量检测试卷A
文档属性
| 名称 | 北师大版2022--2023八年级(上)数学第四单元质量检测试卷A |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 21:59:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2022-20203年八年级(上)第四章一次函数检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
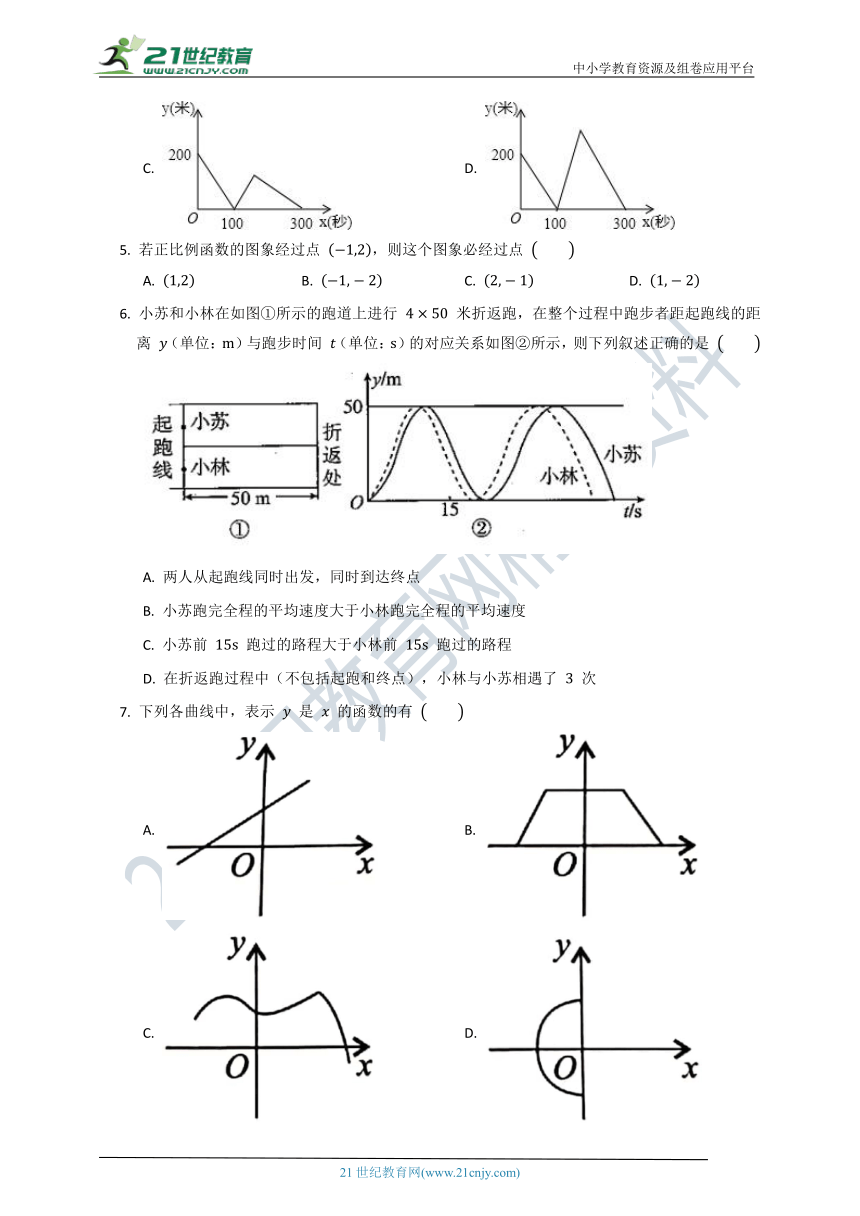
1. 已知 , 两地相距 千米,小黄从 地到 地,平均速度为 千米/时,若用 表示行走的时间(小时), 表示余下的路程(千米),则 关于 的函数解析式是
A. B.
C. D.
2. 根据下表中 与 的几组对应值画出的函数图象是
A. B.
C. D.
3. 直线 经过点 ,则该直线的解析式是
A. B. C. D.
4. 甲、乙两位运动员在一段 米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面 米,他们同时同向出发匀速前进,甲的速度是 米/秒,乙的速度是 米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是 米,比赛时间是 秒,当两人都到达终点计时结束,整个过程中 与 之间的函数图象是
A. B.
C. D.
5. 若正比例函数的图象经过点 ,则这个图象必经过点
A. B. C. D.
6. 小苏和小林在如图①所示的跑道上进行 米折返跑,在整个过程中跑步者距起跑线的距离 (单位:)与跑步时间 (单位:)的对应关系如图②所示,则下列叙述正确的是
A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑完全程的平均速度大于小林跑完全程的平均速度
C. 小苏前 跑过的路程大于小林前 跑过的路程
D. 在折返跑过程中(不包括起跑和终点),小林与小苏相遇了 次
7. 下列各曲线中,表示 是 的函数的有
A. B.
C. D.
8. 在函数 中,自变量 的取值范围是
A. B. 且
C. D.
9. 【例 】如图,直线 过点 ,,则关于 的方程 的解是
A. B. C. D.
10. 下列四个命题中,错误的是
A. 正比例函数是一次函数
B. 反比例函数不是一次函数
C. 一次函数也是正比例函数
D. 如果 与 成正比例,则 与 的关系是一次函数
11. 某日江西省遭受台风袭击,大部分地区发生强降雨.某条河流因受到暴雨影响,水位急剧上升,下表为这一天的水位记录数据,观察表中数据,水位上升最快的时间段是
A. 时到 时 B. 时到 时 C. 时到 时 D. 时到 时
12. 直线 与直线 在同一坐标系中的大致位置是
A. B.
C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 如果一个一次函数满足以下两个条件:()函数值 随着自变量 的值增大而减小;()图象经过点 .那么这个一次函数的解析式可以是 (写出一个即可).
14. 在如图所示的图象中, 是 的函数.
15. 关于 的一次函数 ,为使其成为正比例函数,则 .
16. 在函数 中,自变量 的取值范围是 .
17. 如图 ,点 从 的顶点 出发,沿 匀速运动到点 ,图 是点 运动时,线段 的长度 随时间 变化的关系图象,其中 为曲线部分的最低点,则 的面积是 .
18. 为庆祝建校 周年,某学校组织文艺汇演,八年级排练队形为 排,第一排 人,后面每排比前一排多 人,则每排人数 与排数 之间函数关系式为 .
三、解答题(共7小题;共60分)
19. (8分)根据下列条件,确定直线的表达式:
(1)直线经过 , 两点;
(2)直线经过点 ,它与 轴的交点的横坐标为 .
20.(8分) 画出函数 的图象,并指出 随 的变化规律.
21.(8分)下列函数中, 是自变量, 是 的函数,哪些是一次函数
();();();().
22.(8分) 已知:一次函数 ,求:
(1) 为何值时, 随 的增大而增大
(2) 为何值时,函数图象与 轴的交点在 轴上方
(3) 为何值时,图象不经过第四象限
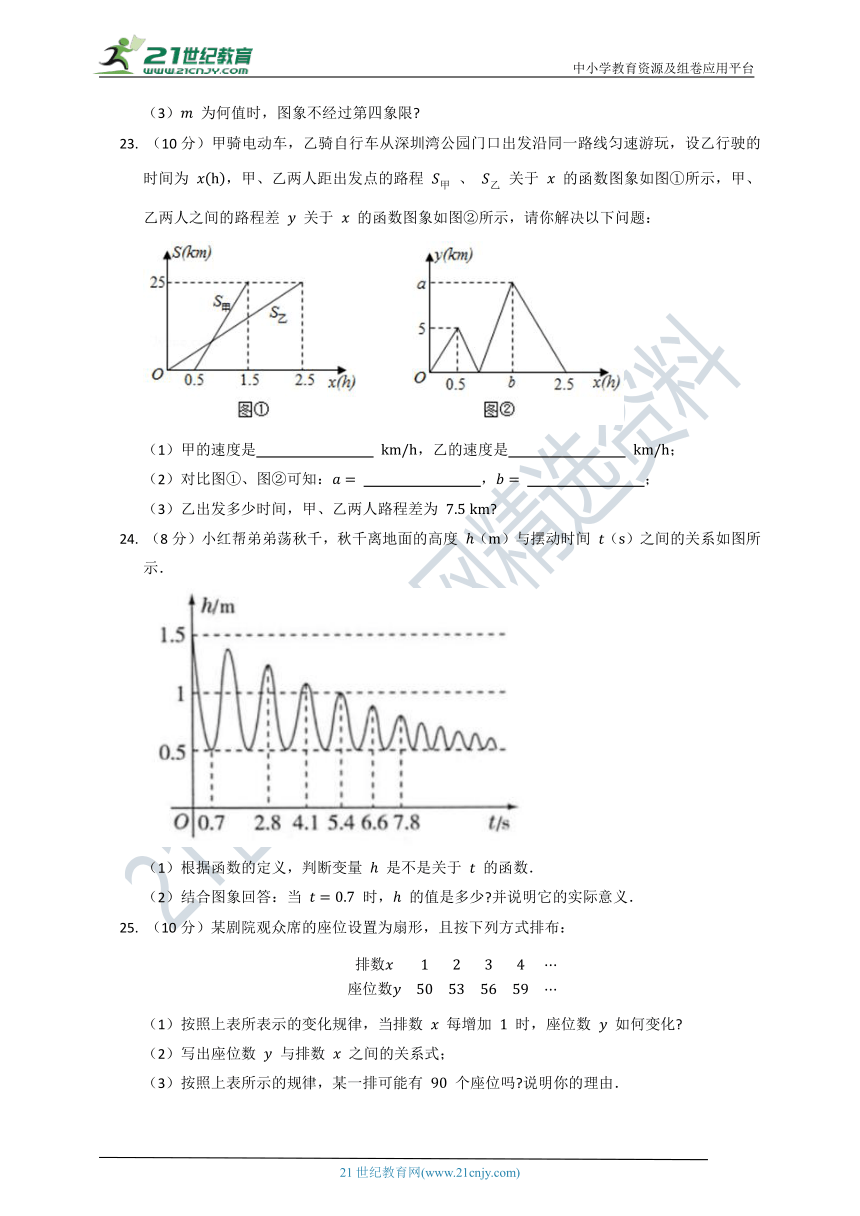
23. (10分)甲骑电动车,乙骑自行车从深圳湾公园门口出发沿同一路线匀速游玩,设乙行驶的时间为 ,甲、乙两人距出发点的路程 、 关于 的函数图象如图①所示,甲、乙两人之间的路程差 关于 的函数图象如图②所示,请你解决以下问题:
(1)甲的速度是 ,乙的速度是 ;
(2)对比图①、图②可知: , ;
(3)乙出发多少时间,甲、乙两人路程差为
24. (8分)小红帮弟弟荡秋千,秋千离地面的高度 ()与摆动时间 ()之间的关系如图所示.
(1)根据函数的定义,判断变量 是不是关于 的函数.
(2)结合图象回答:当 时, 的值是多少 并说明它的实际意义.
25. (10分)某剧院观众席的座位设置为扇形,且按下列方式排布:
(1)按照上表所表示的变化规律,当排数 每增加 时,座位数 如何变化
(2)写出座位数 与排数 之间的关系式;
(3)按照上表所示的规律,某一排可能有 个座位吗 说明你的理由.
答案
第一部分
1. D
【解析】根据题意得走完全程需要的时间为 小时,
.故选D.
2. A
3. A
4. B
【解析】当甲跑到终点时所用的时间为:(秒),
此时甲乙间的距离为:(米),
乙到达终点时所用的时间为:(秒),
最高点坐标为 .
设 关于 的函数解析式为 ,
当 时,有 解得:
此时 ;
当 时,有 解得:
此时 ;
当 时,有 解得:
此时 .
关于 的函数解析式为 .
整个过程中 与之间的函数图象是B.
5. D
6. D
7. C
8. D
【解析】由题意得,,解得 .
9. A
【解析】 直线 过点 ,
即当 时,,
关于 的方程 的解是 .
故选:A.
10. C
11. D
【解析】由题表可知,每 小时记录一次水位的数据,在 时到 时时,水位上升最快,故选D.
12. C
【解析】根据一次函数的系数与图象的关系依次分析选项可得:
A.由图可得, 中,,, 中,,, 的取值矛盾,故本选项错误;
B.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误;
C.由图可得, 中,,, 中,,,, 的取值相一致,故本选项正确;
D.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误.
故选:C.
第二部分
13. (答案不唯一)
14. ,
【解析】给定 的一个值, 可能有两个值与之对应,不符合函数的唯一性,
所以本题中, 不是 的函数,但给定 的一个值(在 的取值范围内), 均有唯一的值与它对应,
所以 是 的函数.
15.
16. 且
17.
【解析】根据图象可知点 在 上运动时,此时 不断增大,
由图象可知:点 从 向 运动时, 的最大值为 ,
即 ,
由于 是曲线部分的最低点,
此时 最小,
即 ,,
此时由勾股定理可知:,
由于图象的曲线部分是轴对称图形,
,
,
的面积为:.
18. (,且 为整数)
【解析】根据“排练队形为 排,第一排 人,后面每排比前一排多 人”可列出 与 之间的关系式为 (,且 为整数).
第三部分
19. (1) 设 (, 是常数,且 ).
直线经过 , 两点,
得
直线的表达式是 .
(2) 设 (, 是常数,且 ).
直线经过 , 两点,
得
直线的表达式是 .
20. 列表得:
图象为:
随着 的增加而减小.
21. 一次函数可以表示为 (, 为常数,)的形式.
()中,,,
是一次函数;
()中,
不是整式,故 不是一次函数;
()中,,,
是一次函数;
()中, 的次数是 ,
不是一次函数.
()()是一次函数.
22. (1) .
(2) .
(3) .
23. (1) ;
【解析】由图可得,
甲的速度为:,乙的速度为:.
(2) ;
【解析】由图可得,
,
.
(3) 由题意可得,
前 ,乙行驶的路程为:,
则甲、乙两人路程差为 是在甲乙相遇之后,
设乙出发 时,甲、乙两人路程差为 ,
,
解得,,
,得 ;即乙出发 或 时,甲、乙两人路程差为 .
24. (1) 由题中图象可知,对于每一个摆动时间 , 都有唯一确定的值与其对应,所以变量 是关于 的函数.
(2) 由题中图象可知,当 时,.它的实际意义是秋千摆动 时,离地面的高度是 .
25. (1) 由表格可知,当排数 每增加 时,座位数 增加 .
(2) 由题意可得 ,
即座位数 与排数 之间的关系式是 .
(3) 按照题表所示的规律,某一排不可能有 个座位.
理由:当 时,,得 ,不合题意,
所以某一排不可能有 个座位.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-20203年八年级(上)第四章一次函数检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 已知 , 两地相距 千米,小黄从 地到 地,平均速度为 千米/时,若用 表示行走的时间(小时), 表示余下的路程(千米),则 关于 的函数解析式是
A. B.
C. D.
2. 根据下表中 与 的几组对应值画出的函数图象是
A. B.
C. D.
3. 直线 经过点 ,则该直线的解析式是
A. B. C. D.
4. 甲、乙两位运动员在一段 米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面 米,他们同时同向出发匀速前进,甲的速度是 米/秒,乙的速度是 米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是 米,比赛时间是 秒,当两人都到达终点计时结束,整个过程中 与 之间的函数图象是
A. B.
C. D.
5. 若正比例函数的图象经过点 ,则这个图象必经过点
A. B. C. D.
6. 小苏和小林在如图①所示的跑道上进行 米折返跑,在整个过程中跑步者距起跑线的距离 (单位:)与跑步时间 (单位:)的对应关系如图②所示,则下列叙述正确的是
A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑完全程的平均速度大于小林跑完全程的平均速度
C. 小苏前 跑过的路程大于小林前 跑过的路程
D. 在折返跑过程中(不包括起跑和终点),小林与小苏相遇了 次
7. 下列各曲线中,表示 是 的函数的有
A. B.
C. D.
8. 在函数 中,自变量 的取值范围是
A. B. 且
C. D.
9. 【例 】如图,直线 过点 ,,则关于 的方程 的解是
A. B. C. D.
10. 下列四个命题中,错误的是
A. 正比例函数是一次函数
B. 反比例函数不是一次函数
C. 一次函数也是正比例函数
D. 如果 与 成正比例,则 与 的关系是一次函数
11. 某日江西省遭受台风袭击,大部分地区发生强降雨.某条河流因受到暴雨影响,水位急剧上升,下表为这一天的水位记录数据,观察表中数据,水位上升最快的时间段是
A. 时到 时 B. 时到 时 C. 时到 时 D. 时到 时
12. 直线 与直线 在同一坐标系中的大致位置是
A. B.
C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 如果一个一次函数满足以下两个条件:()函数值 随着自变量 的值增大而减小;()图象经过点 .那么这个一次函数的解析式可以是 (写出一个即可).
14. 在如图所示的图象中, 是 的函数.
15. 关于 的一次函数 ,为使其成为正比例函数,则 .
16. 在函数 中,自变量 的取值范围是 .
17. 如图 ,点 从 的顶点 出发,沿 匀速运动到点 ,图 是点 运动时,线段 的长度 随时间 变化的关系图象,其中 为曲线部分的最低点,则 的面积是 .
18. 为庆祝建校 周年,某学校组织文艺汇演,八年级排练队形为 排,第一排 人,后面每排比前一排多 人,则每排人数 与排数 之间函数关系式为 .
三、解答题(共7小题;共60分)
19. (8分)根据下列条件,确定直线的表达式:
(1)直线经过 , 两点;
(2)直线经过点 ,它与 轴的交点的横坐标为 .
20.(8分) 画出函数 的图象,并指出 随 的变化规律.
21.(8分)下列函数中, 是自变量, 是 的函数,哪些是一次函数
();();();().
22.(8分) 已知:一次函数 ,求:
(1) 为何值时, 随 的增大而增大
(2) 为何值时,函数图象与 轴的交点在 轴上方
(3) 为何值时,图象不经过第四象限
23. (10分)甲骑电动车,乙骑自行车从深圳湾公园门口出发沿同一路线匀速游玩,设乙行驶的时间为 ,甲、乙两人距出发点的路程 、 关于 的函数图象如图①所示,甲、乙两人之间的路程差 关于 的函数图象如图②所示,请你解决以下问题:
(1)甲的速度是 ,乙的速度是 ;
(2)对比图①、图②可知: , ;
(3)乙出发多少时间,甲、乙两人路程差为
24. (8分)小红帮弟弟荡秋千,秋千离地面的高度 ()与摆动时间 ()之间的关系如图所示.
(1)根据函数的定义,判断变量 是不是关于 的函数.
(2)结合图象回答:当 时, 的值是多少 并说明它的实际意义.
25. (10分)某剧院观众席的座位设置为扇形,且按下列方式排布:
(1)按照上表所表示的变化规律,当排数 每增加 时,座位数 如何变化
(2)写出座位数 与排数 之间的关系式;
(3)按照上表所示的规律,某一排可能有 个座位吗 说明你的理由.
答案
第一部分
1. D
【解析】根据题意得走完全程需要的时间为 小时,
.故选D.
2. A
3. A
4. B
【解析】当甲跑到终点时所用的时间为:(秒),
此时甲乙间的距离为:(米),
乙到达终点时所用的时间为:(秒),
最高点坐标为 .
设 关于 的函数解析式为 ,
当 时,有 解得:
此时 ;
当 时,有 解得:
此时 ;
当 时,有 解得:
此时 .
关于 的函数解析式为 .
整个过程中 与之间的函数图象是B.
5. D
6. D
7. C
8. D
【解析】由题意得,,解得 .
9. A
【解析】 直线 过点 ,
即当 时,,
关于 的方程 的解是 .
故选:A.
10. C
11. D
【解析】由题表可知,每 小时记录一次水位的数据,在 时到 时时,水位上升最快,故选D.
12. C
【解析】根据一次函数的系数与图象的关系依次分析选项可得:
A.由图可得, 中,,, 中,,, 的取值矛盾,故本选项错误;
B.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误;
C.由图可得, 中,,, 中,,,, 的取值相一致,故本选项正确;
D.由图可得, 中,,, 中,,, 的取值相矛盾,故本选项错误.
故选:C.
第二部分
13. (答案不唯一)
14. ,
【解析】给定 的一个值, 可能有两个值与之对应,不符合函数的唯一性,
所以本题中, 不是 的函数,但给定 的一个值(在 的取值范围内), 均有唯一的值与它对应,
所以 是 的函数.
15.
16. 且
17.
【解析】根据图象可知点 在 上运动时,此时 不断增大,
由图象可知:点 从 向 运动时, 的最大值为 ,
即 ,
由于 是曲线部分的最低点,
此时 最小,
即 ,,
此时由勾股定理可知:,
由于图象的曲线部分是轴对称图形,
,
,
的面积为:.
18. (,且 为整数)
【解析】根据“排练队形为 排,第一排 人,后面每排比前一排多 人”可列出 与 之间的关系式为 (,且 为整数).
第三部分
19. (1) 设 (, 是常数,且 ).
直线经过 , 两点,
得
直线的表达式是 .
(2) 设 (, 是常数,且 ).
直线经过 , 两点,
得
直线的表达式是 .
20. 列表得:
图象为:
随着 的增加而减小.
21. 一次函数可以表示为 (, 为常数,)的形式.
()中,,,
是一次函数;
()中,
不是整式,故 不是一次函数;
()中,,,
是一次函数;
()中, 的次数是 ,
不是一次函数.
()()是一次函数.
22. (1) .
(2) .
(3) .
23. (1) ;
【解析】由图可得,
甲的速度为:,乙的速度为:.
(2) ;
【解析】由图可得,
,
.
(3) 由题意可得,
前 ,乙行驶的路程为:,
则甲、乙两人路程差为 是在甲乙相遇之后,
设乙出发 时,甲、乙两人路程差为 ,
,
解得,,
,得 ;即乙出发 或 时,甲、乙两人路程差为 .
24. (1) 由题中图象可知,对于每一个摆动时间 , 都有唯一确定的值与其对应,所以变量 是关于 的函数.
(2) 由题中图象可知,当 时,.它的实际意义是秋千摆动 时,离地面的高度是 .
25. (1) 由表格可知,当排数 每增加 时,座位数 增加 .
(2) 由题意可得 ,
即座位数 与排数 之间的关系式是 .
(3) 按照题表所示的规律,某一排不可能有 个座位.
理由:当 时,,得 ,不合题意,
所以某一排不可能有 个座位.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
