第四章 一次函数单元质量检测试卷B(含解析)
文档属性
| 名称 | 第四章 一次函数单元质量检测试卷B(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2022-2023学年八年级(上)第四章一次函数检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 若函数 的图象经过 点,那么它一定经过
A. B. C. D.
2. 某地海拔高度 与温度 的关系可用 来表示(其中温度单位为 ,高度单位为 ),则该地区海拔高度为 的山顶上的温度是
A. B. C. D.
3. 正比例函数 的图象如图所示,则 的值为
A. B. C. D.
4. 函数 的自变量 的取值范围是
A. B. 且
C. D. 且
5. 若一次函数 的图象经过原点,则
A. B. C. D.
6. 下列曲线中不能表示 是 的函数的是
A. B.
C. D.
7. 一根蜡烛长 ,点燃后每小时燃烧 ,燃烧中剩下的长度 和燃烧的时间 (小时)之间的函数关系用图象表示为
A. B.
C. D.
8. 在 ,, 三个数中任取两个组成一个两位数,则组成的两位数是完全平方数的概率是
A. B. C. D.
9. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用 , 分别表示乌龟和兔子赛跑的路程, 为赛跑时间,则下列图象中与故事情节相吻合的是
A. B.
C. D.
10. 已知一次函数和,函数和的图象可能是
A. B.
C. D.
11. 如图,一次函数 和 的图象正确的是
A. B.
C. D.
12. 如果直线 与两坐标轴围成的三角形的面积是 ,那么 的值是
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 在平面直角坐标系 中,点 在正比例函数 的图象上,则点 位于第 象限.
14. 已知一次函数 的图象过点 ,那么当 的值增大时, 的值随之 (填“增大”或“减小”).
15. 一天早晨,小玲从家出发匀速步行到学校.小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲.妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半.小玲继续以原速度步行前往学校.妈妈与小玲之间的距离 (米)与小玲从家出发后步行的时间 (分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为 米.
16. 已知 ,,则函数 的图象经过的象限为 象限.
17. 函数 的图象交 轴于点 ,交 轴于点 ,则 , 两点间的距离为
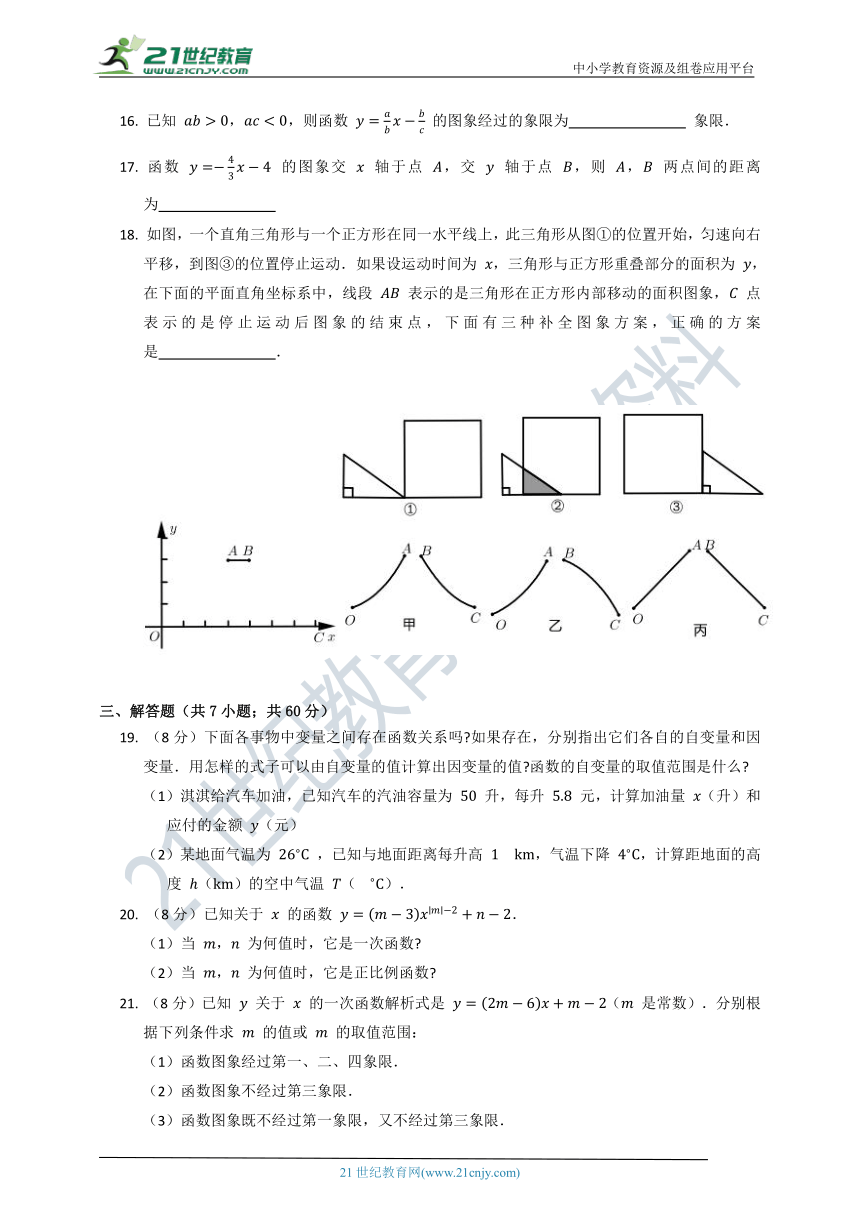
18. 如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为 ,三角形与正方形重叠部分的面积为 ,在下面的平面直角坐标系中,线段 表示的是三角形在正方形内部移动的面积图象, 点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 .
三、解答题(共7小题;共60分)
19. (8分)下面各事物中变量之间存在函数关系吗 如果存在,分别指出它们各自的自变量和因变量.用怎样的式子可以由自变量的值计算出因变量的值 函数的自变量的取值范围是什么
(1)淇淇给汽车加油,已知汽车的汽油容量为 升,每升 元,计算加油量 (升)和应付的金额 (元)
(2)某地面气温为 ,已知与地面距离每升高 ,气温下降 ,计算距地面的高度 ()的空中气温 ().
20. (8分)已知关于 的函数 .
(1)当 , 为何值时,它是一次函数
(2)当 , 为何值时,它是正比例函数
21. (8分)已知 关于 的一次函数解析式是 ( 是常数).分别根据下列条件求 的值或 的取值范围:
(1)函数图象经过第一、二、四象限.
(2)函数图象不经过第三象限.
(3)函数图象既不经过第一象限,又不经过第三象限.
22. (8分)一水箱中有水 升,现在往外放水,每分钟放水 升,请用三种不同的方法表示水箱中剩余水量 (升)与放水时间 (分钟)之间的函数关系.
23. (8分)根据数学家凯勒的“百米赛跑数学模型”,前 米称为“加速期”, 米 米为“中途期”, 米 米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度 与路程 之间的观测数据,绘制成曲线如图所示.
(1) 是关于 的函数吗 为什么
(2)“加速期”结束时,小斌的速度为多少
(3)根据如图提供的信息,给小斌提一条训练建议.
24. (10分)由于持续干旱,某水库的蓄水量随着时间的增加而减少.干旱时间 (天)与蓄水量 (万立方米)的关系如图所示,试回答下列问题:
(1)写出 与 的函数解析式.
(2)若干旱持续 天,水库的蓄水量还剩多少
(3)蓄水量小于 万立方米时,将发出严重干旱警报,试问干旱持续多少天后将发出严重干旱警报.
(4)按照图中显示的规律,干旱持续多少天水库将干涸
25.(10分) 某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前 个小时为生产磨合期, 个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式.他们每人生产的零件总数 (个)与生产时间 (小时)的关系如图所示.根据图象回答:
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时
(2)当 为多少时,甲、乙所生产的零件个数第一次相等 甲、乙中,谁先完成一天的生产任务
(3)设备改良升级后每小时生产零件的个数是多少 与另一工人的正常生产速度相比每小时多生产几个
答案
第一部分
1. B
【解析】把点 代入 中,得 ;
A、 ;
B、 ;
C、 ;
D、 .
2. D
【解析】,
时,
该地区海拔高度为 米的山顶上的温度是 .
故选:D.
3. B
【解析】由题图知,点 在函数 的图象上,
,解得 ,
故选B.
4. D
5. A
【解析】 一次函数 的图象经过原点,
,且 ,
.
6. C
7. C
8. B
【解析】在 ,, 三个数中任取两个组成一个两位数,有 种结果:,,,,,,其中 和 是完全平方数,所以组成的两位数是完全平方数的概率是 .故选B.
9. C
10. A
【解析】【分析】根据直线①判断出、的符号,然后根据、的符号判断出直线②经过的象限即可,做出判断.
【解析】解:、由①可知:,.
直线②经过一、二、三象限,故正确;
、由①可知:,.
直线②经过一、二、三象限,故错误;
、由①可知:,.
直线②经过一、二、四象限,交点不对,故错误;
、由①可知:,,
直线②经过二、三、四象限,故错误.
故选:.
【点评】本题主要考查的是一次函数的图象和性质,掌握一次函数的图象和性质是解题的关键.
11. C
12. C
第二部分
13. 四
14. 增大
15.
16. 一、二、三
17.
【解析】由题意可得 , 两点的坐标分别为 ,.
由勾股定理得 .
18. 乙
【解析】设三角形的底为 ,高为 与正方形重叠部分的高为 ,速度为 ,正方形边长为 ,
由图②可知,当三角形进入正方形时,易知 ,则有 ,
( 为常数),且 ,
故阴影部分面积 和时间 是一个开口向上的二次函数,
当三角形开始离开正方形时,,故 ,
,
,,, 都为常数,
阴影部分面积 和时间 是一个开口向下的二次函数.
综上所述正确的答案为乙.
第三部分
19. (1) 存在函数关系.自变量是加油量 (升),因变量是应付的金额 (元),,.
(2) 存在函数关系.自变量是距地面的高度 (),因变量是空中的气温 (),,.
20. (1) 由题意知 ,且 ,解得 ,故当 , 为任意实数时,它是一次函数.
(2) 由题意知 , 且 ,解得 ,,故当 , 时,它是正比例函数.
21. (1) .
(2) .
(3) .
22. ()解析法:函数表达式为 .
()列表法:表格如下 .
()图象法:如图所示.
23. (1) 是 的函数,在这个变化过程中,对于 的每一个确定的值, 都有唯一确定的值与之对应.
(2) “加速期”结束时,小斌的速度为 .
(3) 答案不唯一.例如:根据图象信息,小斌在 米左右时速度下降明显,建议增加耐力训练,提高成绩.
24. (1) ;
(2) 还剩 万立方米;
(3) 天;
(4) 天.
25. (1) 由图象可知:在生产的过程中,甲进行了改良,停止生产时间: 小时.
(2) 由图象可知,当 时,甲和乙第一次生产零件的个数相同;甲、乙中,甲先完成一天的生产任务.
(3) 设备改良升级后,甲每小时生产零件的个数是: 个;
乙每小时生产零件的个数是: 个;
因此,改良后,甲每小时比乙多生产: 个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-2023学年八年级(上)第四章一次函数检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 若函数 的图象经过 点,那么它一定经过
A. B. C. D.
2. 某地海拔高度 与温度 的关系可用 来表示(其中温度单位为 ,高度单位为 ),则该地区海拔高度为 的山顶上的温度是
A. B. C. D.
3. 正比例函数 的图象如图所示,则 的值为
A. B. C. D.
4. 函数 的自变量 的取值范围是
A. B. 且
C. D. 且
5. 若一次函数 的图象经过原点,则
A. B. C. D.
6. 下列曲线中不能表示 是 的函数的是
A. B.
C. D.
7. 一根蜡烛长 ,点燃后每小时燃烧 ,燃烧中剩下的长度 和燃烧的时间 (小时)之间的函数关系用图象表示为
A. B.
C. D.
8. 在 ,, 三个数中任取两个组成一个两位数,则组成的两位数是完全平方数的概率是
A. B. C. D.
9. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用 , 分别表示乌龟和兔子赛跑的路程, 为赛跑时间,则下列图象中与故事情节相吻合的是
A. B.
C. D.
10. 已知一次函数和,函数和的图象可能是
A. B.
C. D.
11. 如图,一次函数 和 的图象正确的是
A. B.
C. D.
12. 如果直线 与两坐标轴围成的三角形的面积是 ,那么 的值是
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 在平面直角坐标系 中,点 在正比例函数 的图象上,则点 位于第 象限.
14. 已知一次函数 的图象过点 ,那么当 的值增大时, 的值随之 (填“增大”或“减小”).
15. 一天早晨,小玲从家出发匀速步行到学校.小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲.妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半.小玲继续以原速度步行前往学校.妈妈与小玲之间的距离 (米)与小玲从家出发后步行的时间 (分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为 米.
16. 已知 ,,则函数 的图象经过的象限为 象限.
17. 函数 的图象交 轴于点 ,交 轴于点 ,则 , 两点间的距离为
18. 如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为 ,三角形与正方形重叠部分的面积为 ,在下面的平面直角坐标系中,线段 表示的是三角形在正方形内部移动的面积图象, 点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 .
三、解答题(共7小题;共60分)
19. (8分)下面各事物中变量之间存在函数关系吗 如果存在,分别指出它们各自的自变量和因变量.用怎样的式子可以由自变量的值计算出因变量的值 函数的自变量的取值范围是什么
(1)淇淇给汽车加油,已知汽车的汽油容量为 升,每升 元,计算加油量 (升)和应付的金额 (元)
(2)某地面气温为 ,已知与地面距离每升高 ,气温下降 ,计算距地面的高度 ()的空中气温 ().
20. (8分)已知关于 的函数 .
(1)当 , 为何值时,它是一次函数
(2)当 , 为何值时,它是正比例函数
21. (8分)已知 关于 的一次函数解析式是 ( 是常数).分别根据下列条件求 的值或 的取值范围:
(1)函数图象经过第一、二、四象限.
(2)函数图象不经过第三象限.
(3)函数图象既不经过第一象限,又不经过第三象限.
22. (8分)一水箱中有水 升,现在往外放水,每分钟放水 升,请用三种不同的方法表示水箱中剩余水量 (升)与放水时间 (分钟)之间的函数关系.
23. (8分)根据数学家凯勒的“百米赛跑数学模型”,前 米称为“加速期”, 米 米为“中途期”, 米 米为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度 与路程 之间的观测数据,绘制成曲线如图所示.
(1) 是关于 的函数吗 为什么
(2)“加速期”结束时,小斌的速度为多少
(3)根据如图提供的信息,给小斌提一条训练建议.
24. (10分)由于持续干旱,某水库的蓄水量随着时间的增加而减少.干旱时间 (天)与蓄水量 (万立方米)的关系如图所示,试回答下列问题:
(1)写出 与 的函数解析式.
(2)若干旱持续 天,水库的蓄水量还剩多少
(3)蓄水量小于 万立方米时,将发出严重干旱警报,试问干旱持续多少天后将发出严重干旱警报.
(4)按照图中显示的规律,干旱持续多少天水库将干涸
25.(10分) 某车间的甲、乙两名工人分别同时生产同种零件,在开始生产的前 个小时为生产磨合期, 个小时后有一人停工一段时间对设备进行改良升级,以提升生产效率,另一人进入正常的生产模式.他们每人生产的零件总数 (个)与生产时间 (小时)的关系如图所示.根据图象回答:
(1)在生产过程中,哪位工人对设备进行改良升级,停止生产多少小时
(2)当 为多少时,甲、乙所生产的零件个数第一次相等 甲、乙中,谁先完成一天的生产任务
(3)设备改良升级后每小时生产零件的个数是多少 与另一工人的正常生产速度相比每小时多生产几个
答案
第一部分
1. B
【解析】把点 代入 中,得 ;
A、 ;
B、 ;
C、 ;
D、 .
2. D
【解析】,
时,
该地区海拔高度为 米的山顶上的温度是 .
故选:D.
3. B
【解析】由题图知,点 在函数 的图象上,
,解得 ,
故选B.
4. D
5. A
【解析】 一次函数 的图象经过原点,
,且 ,
.
6. C
7. C
8. B
【解析】在 ,, 三个数中任取两个组成一个两位数,有 种结果:,,,,,,其中 和 是完全平方数,所以组成的两位数是完全平方数的概率是 .故选B.
9. C
10. A
【解析】【分析】根据直线①判断出、的符号,然后根据、的符号判断出直线②经过的象限即可,做出判断.
【解析】解:、由①可知:,.
直线②经过一、二、三象限,故正确;
、由①可知:,.
直线②经过一、二、三象限,故错误;
、由①可知:,.
直线②经过一、二、四象限,交点不对,故错误;
、由①可知:,,
直线②经过二、三、四象限,故错误.
故选:.
【点评】本题主要考查的是一次函数的图象和性质,掌握一次函数的图象和性质是解题的关键.
11. C
12. C
第二部分
13. 四
14. 增大
15.
16. 一、二、三
17.
【解析】由题意可得 , 两点的坐标分别为 ,.
由勾股定理得 .
18. 乙
【解析】设三角形的底为 ,高为 与正方形重叠部分的高为 ,速度为 ,正方形边长为 ,
由图②可知,当三角形进入正方形时,易知 ,则有 ,
( 为常数),且 ,
故阴影部分面积 和时间 是一个开口向上的二次函数,
当三角形开始离开正方形时,,故 ,
,
,,, 都为常数,
阴影部分面积 和时间 是一个开口向下的二次函数.
综上所述正确的答案为乙.
第三部分
19. (1) 存在函数关系.自变量是加油量 (升),因变量是应付的金额 (元),,.
(2) 存在函数关系.自变量是距地面的高度 (),因变量是空中的气温 (),,.
20. (1) 由题意知 ,且 ,解得 ,故当 , 为任意实数时,它是一次函数.
(2) 由题意知 , 且 ,解得 ,,故当 , 时,它是正比例函数.
21. (1) .
(2) .
(3) .
22. ()解析法:函数表达式为 .
()列表法:表格如下 .
()图象法:如图所示.
23. (1) 是 的函数,在这个变化过程中,对于 的每一个确定的值, 都有唯一确定的值与之对应.
(2) “加速期”结束时,小斌的速度为 .
(3) 答案不唯一.例如:根据图象信息,小斌在 米左右时速度下降明显,建议增加耐力训练,提高成绩.
24. (1) ;
(2) 还剩 万立方米;
(3) 天;
(4) 天.
25. (1) 由图象可知:在生产的过程中,甲进行了改良,停止生产时间: 小时.
(2) 由图象可知,当 时,甲和乙第一次生产零件的个数相同;甲、乙中,甲先完成一天的生产任务.
(3) 设备改良升级后,甲每小时生产零件的个数是: 个;
乙每小时生产零件的个数是: 个;
因此,改良后,甲每小时比乙多生产: 个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
