第四章 一次函数单元质量检测试卷C(含解析)
文档属性
| 名称 | 第四章 一次函数单元质量检测试卷C(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版2022-2023学年八年级(上)第四章一次函数检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 已知一次函数 的图象不经过第二象限,那么 的取值范围是
A. B. C. D.
2. 若 与 成正比例,则
A. 是 的一次函数 B. 与 没有函数关系
C. 是 的函数,但不是一次函数 D. 是 的正比例函数
3. 如图,直线 和直线 相交于点 ,根据图象可知,方程 的解是
A. B. C. D.
4. 下列变量之间的关系是一次函数的是
A. 等边三角形的面积和它的边长
B. 正方体的表面积和它的棱长
C. 匀速行驶的汽车,行驶的路程和行驶时间
D. 面积为 的长方形的长和宽
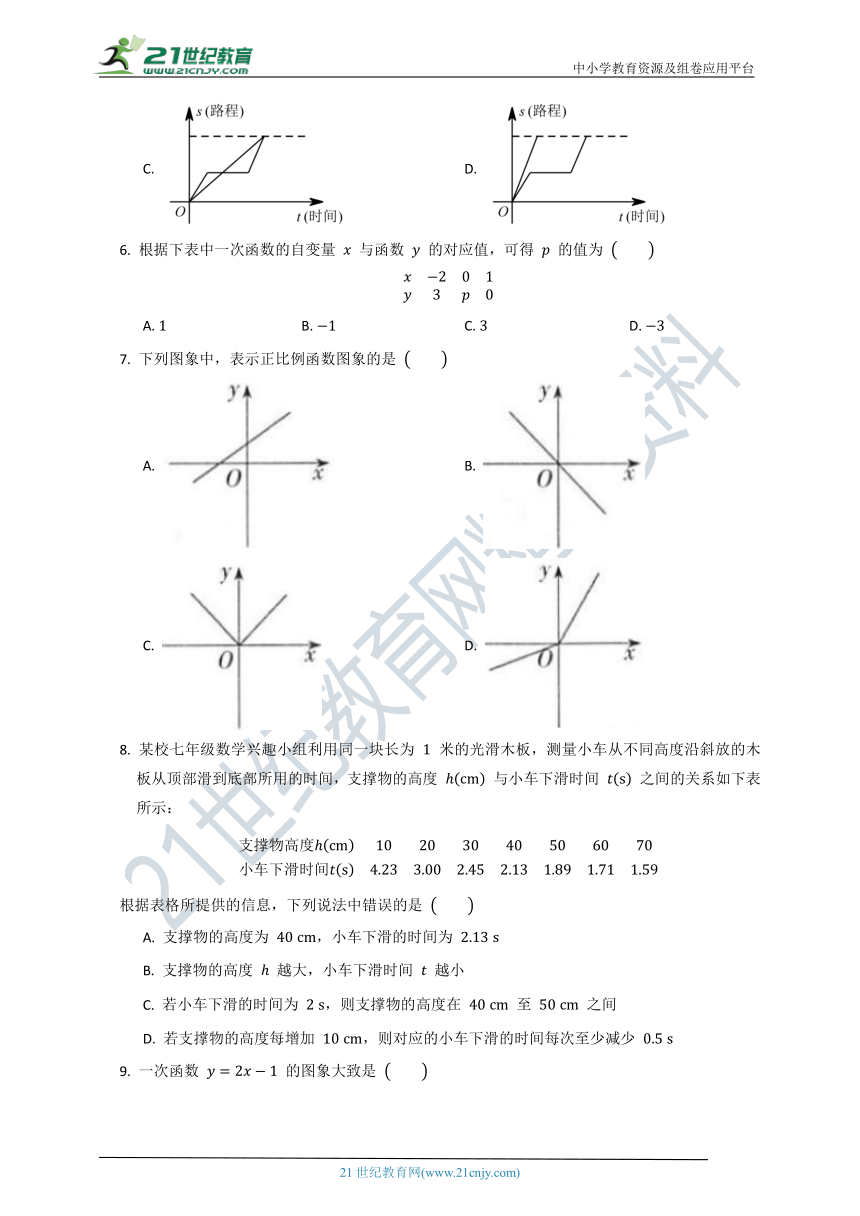
5. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是
A. B.
C. D.
6. 根据下表中一次函数的自变量 与函数 的对应值,可得 的值为
A. B. C. D.
7. 下列图象中,表示正比例函数图象的是
A. B.
C. D.
8. 某校七年级数学兴趣小组利用同一块长为 米的光滑木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物的高度 与小车下滑时间 之间的关系如下表所示:
根据表格所提供的信息,下列说法中错误的是
A. 支撑物的高度为 ,小车下滑的时间为
B. 支撑物的高度 越大,小车下滑时间 越小
C. 若小车下滑的时间为 ,则支撑物的高度在 至 之间
D. 若支撑物的高度每增加 ,则对应的小车下滑的时间每次至少减少
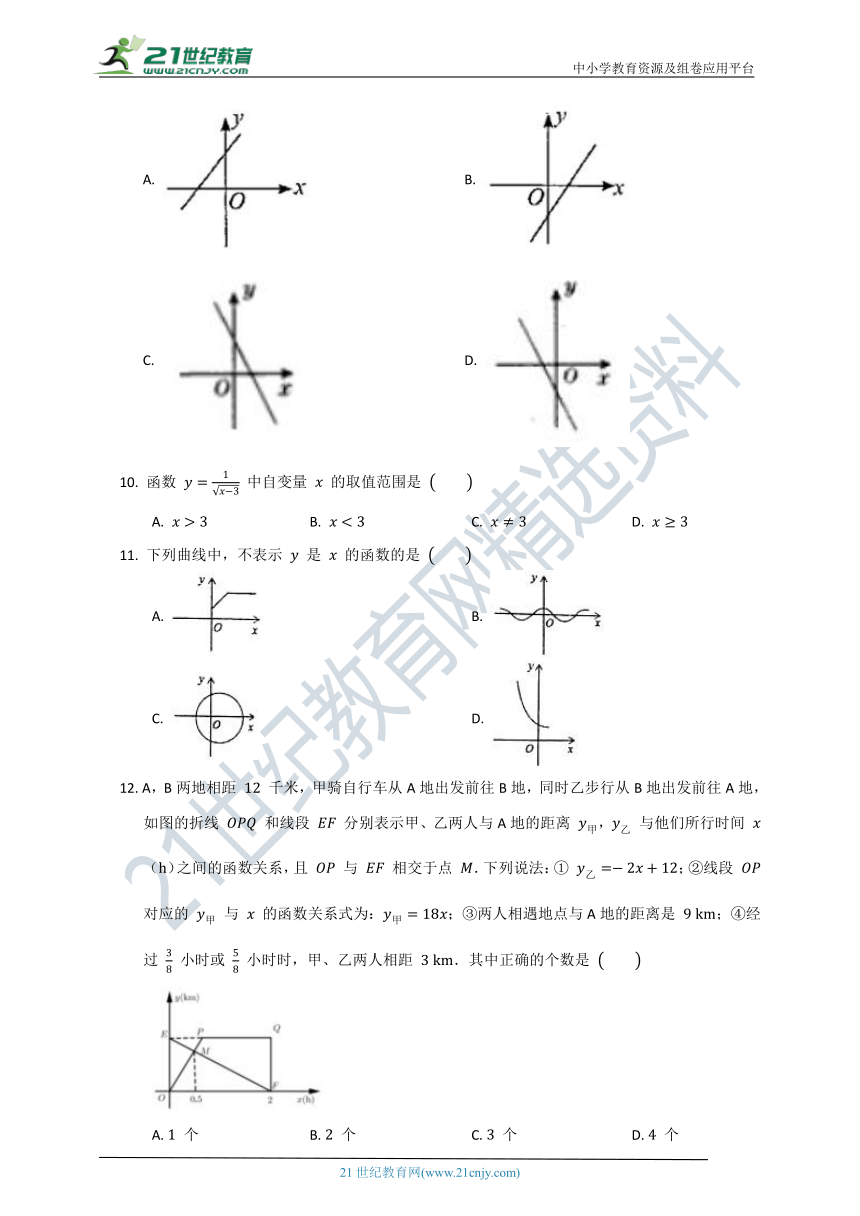
9. 一次函数 的图象大致是
A. B.
C. D.
10. 函数 中自变量 的取值范围是
A. B. C. D.
11. 下列曲线中,不表示 是 的函数的是
A. B.
C. D.
12. A,B两地相距 千米,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线 和线段 分别表示甲、乙两人与A地的距离 , 与他们所行时间 ()之间的函数关系,且 与 相交于点 .下列说法:① ;②线段 对应的 与 的函数关系式为:;③两人相遇地点与A地的距离是 ;④经过 小时或 小时时,甲、乙两人相距 .其中正确的个数是
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;每小题4分,共24分)
13. 已知一次函数 ,当 时,.
14. 函数 的定义域是 .
15. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为 (分钟),所走的路程为 (米), 与 之间的函数关系如图所示.则下列说法中正确的序号为 .
①小明中途休息用了 分钟;
②小明休息前爬山的平均速度为每分钟 米/分钟;
③小明在上述过程中所走的路程为 米;
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
16. 如图,三个正比例函数的图象分别对应解析式:① ,② ,③ ,将 ,, 从小到大排列并用“”连接为 .
17. 对比学习:如图是某市 时到 时的气温变化图,回答下列问题:
() 时,气温为 (即 );
()当时间 满足: 时,气温在 以上(即 );
()当时间 满足: 时,气温在 以下(即 ).
18. 已知 , 的坐标分别为 ,,点 在直线 上,如果 为等腰三角形,那么这样的点 共有 个.
三、解答题(共7小题;共60分)
19. (8分)下列函数(其中 是自变量)中,哪些是正比例函数 哪些不是 为什么
();
();
();
().
20. (8分)已知一次函数 .
(1)求 .
(2)如果 ,求实数 的值;
(3)如果 ,求实数 的值.
21. (8分)小明与小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米,图中 , 分别表示两人在赛跑中的路程与时间的关系(图象不完整).试观察图象并回答下列问题:
(1)哪条线段是表示小明所跑的路程与时间的关系
(2)小明让小亮先跑了多少米
(3)谁会赢得这场比赛
22. (8分)画出下列函数的图象,并求图象与 轴、 轴的交点坐标.
(1);
(2);
(3);
(4).
23. (8分)有这样一个问题:探究函数 的图象与性质.
小菲根据学习函数的经验,对函数 的图象与性质进行了探究.
下面是小菲的探究过程,请补充完整:
(1)函数 的自变量 的取值范围是 .
(2)下表是 与 的几组对应值.
表中 的值为 .
(3)如下图,在平面直角坐标系 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(4)根据画出的函数图象,写出:
① 时,对应的函数值 约为 (结果保留一位小数);
②该函数的一条性质: .
24.(10分) 甲、乙两家商场平时以同样价格出售相同的商品,新冠疫情期间,为了减少库存,甲、乙两家商场打折促销,甲商场所有商品按 折出售,乙商场对一次购物中超过 元后的价格部分打 折.
(1)以 (单位:元)表示商品原价,(单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数关系式;
(2)新冠疫情期间如何选择这两家商场去购物更省钱
25. (10分)如图, 是 与弦 所围成的图形的内部的一定点, 是弦 上一动点,连接 并延长交 于点 ,连接 .已知 ,设 , 两点间的距离为 ,, 两点间的距离为 ,, 两点间的距离为 .
小腾根据学习函数的经验,分别对函数 , 随自变量 的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值;
(2)在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点 ,,并画出函数 , 的图象;
(3)结合函数图象,解决问题:当 为等腰三角形时, 的长度约为 .
答案
第一部分
1. A
2. A
3. A
4. C
【解析】设等边三角形的边长为 ,易得等边三角形的面积 ,故A选项不符合;
设正方体的棱长为 ,则表面积 ,故B选项不符合;
匀速行驶的汽车,行驶的路程 和行驶时间 的关系式为 ,是一次函数;设面积为 的长方形的长和宽分别为 ,,则 ,所以 ,故D选项不符合.
5. B
6. A
【解析】设 ,将表格中对应的 , 的值代入得二元一次方程组,解方程组得 , 的值,回代 时,得到对应的 值即可.
设 , 解得 ,.
,当 时,得 .
7. B
【解析】正比例函数图象是过原点的一条直线.
8. D
【解析】A、由图表可知,当 时,,故A不符合题意;
B、支撑物高度 越大,小车下滑时间 越小,故B不符合题意;
C、若小车下滑时间为 ,则支撑物高度在 至 之间,故C不符合题意;
D、若支撑物的高度每增加 ,则对应的小车下滑的时间每次不一定减少 ,故D符合题意.
9. B
10. A
11. C
【解析】A的图象符合一个 有唯一的 对应,故 是 的函数;
B的图象符合一个 有唯一的 对应,故 是 的函数;
C的图象存在一个 对应两个 的情况,故 不是 的函数;
D的图象符合一个 有唯一的 对应,故 是 的函数.
12. C
【解析】设 与 的函数关系式是 ,
点 , 在函数 的图象上,
解得
即 与 的函数关系式是 ,故①错误;
当 时,,
即两人相遇地点与A地的距离是 ,故③正确;
设线段 对应的 与 的函数关系式是 ,
点 在函数 的图象上,
,
解得 ,
即线段 对应的 与 的函数关系式是 ,故②正确;
令 ,
解得,,,
即经过 小时或 小时,甲、乙两人相距 ,故④正确;
正确的是②③④这 个,
故选C.
第二部分
13.
【解析】把 代入 ,得 ,解得 .
14.
【解析】由题意,,即 .
15. ①②④
【解析】①根据图象可知,在 分钟,路程没有发生变化,所以小明中途休息的时间为 分钟,故正确;
②根据图象可知,当 时,,所以小明休息前爬山的平均速度为:(米/分钟),故正确;
③根据图象可知,小明在上述过程中所走的路程为 米,故错误;
④小明休息后的爬山的平均速度为:(米/分),
小明休息前爬山的平均速度为:(米/分钟),.
所以小明休息前爬山的平均速度大于休息后爬山的平均速度,故正确;
综上所述,正确的有①②④.
16.
17. ,,
18.
【解析】在坐标系中画出直线 及 , 两点,作 的中垂线,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 也有 个交点,
故这样的点 共有 个.
第三部分
19. 正比例函数是 ,;
, 不是正比例函数.
20. (1) .
(2) 由题意得:,.
(3) 由题意得:,.
21. (1) ;
(2) 米;
(3) 小明会赢得比赛.
22. (1) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 ;
(2) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 ;
(3) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 ;
(4) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 .
23. (1)
(2)
【解析】令 ,
,
.
(3) 如图所示:
(4) ① 至
②答案不唯一,如 时, 随 的增大而增大
24. (1) ;
当在乙商场购买商品未超过 元 时,乙商场按照原价售卖,即 ;
当在乙商场购买物品超过 元时,超过部分按 折,
所以 ,化简得 ;
所以 ;.
(2) 由题意可知,当购买商品原价小于等于 时,甲商场打 折,乙商场不打折,所以甲商场购物更加划算;
当购买商品原价超过 元时,
若 ,即 此时甲商场花费更低,购物选择甲商场;
若 ,即 ,此时甲乙商场购物花费一样;
若 ,即 时,此时乙商场花费更低,购物选择乙商场;
综上所述:当购买商品原价金额小于 时,选择甲商场更划算;当购买商品原价金额等于 时,选择甲商场和乙商场购物一样划算;当购买商品原价金额大于 时,选择乙商场更划算.
25. (1) 通过画图观察可得当 时,.
(2) 如图所示.
(3)
【解析】在坐标系中画出直线 ,则三个图象中,两两图象交点的横坐标即为 为等腰三角形时线段 的长度,则 的长度约为 或 或 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-2023学年八年级(上)第四章一次函数检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 已知一次函数 的图象不经过第二象限,那么 的取值范围是
A. B. C. D.
2. 若 与 成正比例,则
A. 是 的一次函数 B. 与 没有函数关系
C. 是 的函数,但不是一次函数 D. 是 的正比例函数
3. 如图,直线 和直线 相交于点 ,根据图象可知,方程 的解是
A. B. C. D.
4. 下列变量之间的关系是一次函数的是
A. 等边三角形的面积和它的边长
B. 正方体的表面积和它的棱长
C. 匀速行驶的汽车,行驶的路程和行驶时间
D. 面积为 的长方形的长和宽
5. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是
A. B.
C. D.
6. 根据下表中一次函数的自变量 与函数 的对应值,可得 的值为
A. B. C. D.
7. 下列图象中,表示正比例函数图象的是
A. B.
C. D.
8. 某校七年级数学兴趣小组利用同一块长为 米的光滑木板,测量小车从不同高度沿斜放的木板从顶部滑到底部所用的时间,支撑物的高度 与小车下滑时间 之间的关系如下表所示:
根据表格所提供的信息,下列说法中错误的是
A. 支撑物的高度为 ,小车下滑的时间为
B. 支撑物的高度 越大,小车下滑时间 越小
C. 若小车下滑的时间为 ,则支撑物的高度在 至 之间
D. 若支撑物的高度每增加 ,则对应的小车下滑的时间每次至少减少
9. 一次函数 的图象大致是
A. B.
C. D.
10. 函数 中自变量 的取值范围是
A. B. C. D.
11. 下列曲线中,不表示 是 的函数的是
A. B.
C. D.
12. A,B两地相距 千米,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线 和线段 分别表示甲、乙两人与A地的距离 , 与他们所行时间 ()之间的函数关系,且 与 相交于点 .下列说法:① ;②线段 对应的 与 的函数关系式为:;③两人相遇地点与A地的距离是 ;④经过 小时或 小时时,甲、乙两人相距 .其中正确的个数是
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;每小题4分,共24分)
13. 已知一次函数 ,当 时,.
14. 函数 的定义域是 .
15. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为 (分钟),所走的路程为 (米), 与 之间的函数关系如图所示.则下列说法中正确的序号为 .
①小明中途休息用了 分钟;
②小明休息前爬山的平均速度为每分钟 米/分钟;
③小明在上述过程中所走的路程为 米;
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
16. 如图,三个正比例函数的图象分别对应解析式:① ,② ,③ ,将 ,, 从小到大排列并用“”连接为 .
17. 对比学习:如图是某市 时到 时的气温变化图,回答下列问题:
() 时,气温为 (即 );
()当时间 满足: 时,气温在 以上(即 );
()当时间 满足: 时,气温在 以下(即 ).
18. 已知 , 的坐标分别为 ,,点 在直线 上,如果 为等腰三角形,那么这样的点 共有 个.
三、解答题(共7小题;共60分)
19. (8分)下列函数(其中 是自变量)中,哪些是正比例函数 哪些不是 为什么
();
();
();
().
20. (8分)已知一次函数 .
(1)求 .
(2)如果 ,求实数 的值;
(3)如果 ,求实数 的值.
21. (8分)小明与小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米,图中 , 分别表示两人在赛跑中的路程与时间的关系(图象不完整).试观察图象并回答下列问题:
(1)哪条线段是表示小明所跑的路程与时间的关系
(2)小明让小亮先跑了多少米
(3)谁会赢得这场比赛
22. (8分)画出下列函数的图象,并求图象与 轴、 轴的交点坐标.
(1);
(2);
(3);
(4).
23. (8分)有这样一个问题:探究函数 的图象与性质.
小菲根据学习函数的经验,对函数 的图象与性质进行了探究.
下面是小菲的探究过程,请补充完整:
(1)函数 的自变量 的取值范围是 .
(2)下表是 与 的几组对应值.
表中 的值为 .
(3)如下图,在平面直角坐标系 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(4)根据画出的函数图象,写出:
① 时,对应的函数值 约为 (结果保留一位小数);
②该函数的一条性质: .
24.(10分) 甲、乙两家商场平时以同样价格出售相同的商品,新冠疫情期间,为了减少库存,甲、乙两家商场打折促销,甲商场所有商品按 折出售,乙商场对一次购物中超过 元后的价格部分打 折.
(1)以 (单位:元)表示商品原价,(单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数关系式;
(2)新冠疫情期间如何选择这两家商场去购物更省钱
25. (10分)如图, 是 与弦 所围成的图形的内部的一定点, 是弦 上一动点,连接 并延长交 于点 ,连接 .已知 ,设 , 两点间的距离为 ,, 两点间的距离为 ,, 两点间的距离为 .
小腾根据学习函数的经验,分别对函数 , 随自变量 的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值;
(2)在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点 ,,并画出函数 , 的图象;
(3)结合函数图象,解决问题:当 为等腰三角形时, 的长度约为 .
答案
第一部分
1. A
2. A
3. A
4. C
【解析】设等边三角形的边长为 ,易得等边三角形的面积 ,故A选项不符合;
设正方体的棱长为 ,则表面积 ,故B选项不符合;
匀速行驶的汽车,行驶的路程 和行驶时间 的关系式为 ,是一次函数;设面积为 的长方形的长和宽分别为 ,,则 ,所以 ,故D选项不符合.
5. B
6. A
【解析】设 ,将表格中对应的 , 的值代入得二元一次方程组,解方程组得 , 的值,回代 时,得到对应的 值即可.
设 , 解得 ,.
,当 时,得 .
7. B
【解析】正比例函数图象是过原点的一条直线.
8. D
【解析】A、由图表可知,当 时,,故A不符合题意;
B、支撑物高度 越大,小车下滑时间 越小,故B不符合题意;
C、若小车下滑时间为 ,则支撑物高度在 至 之间,故C不符合题意;
D、若支撑物的高度每增加 ,则对应的小车下滑的时间每次不一定减少 ,故D符合题意.
9. B
10. A
11. C
【解析】A的图象符合一个 有唯一的 对应,故 是 的函数;
B的图象符合一个 有唯一的 对应,故 是 的函数;
C的图象存在一个 对应两个 的情况,故 不是 的函数;
D的图象符合一个 有唯一的 对应,故 是 的函数.
12. C
【解析】设 与 的函数关系式是 ,
点 , 在函数 的图象上,
解得
即 与 的函数关系式是 ,故①错误;
当 时,,
即两人相遇地点与A地的距离是 ,故③正确;
设线段 对应的 与 的函数关系式是 ,
点 在函数 的图象上,
,
解得 ,
即线段 对应的 与 的函数关系式是 ,故②正确;
令 ,
解得,,,
即经过 小时或 小时,甲、乙两人相距 ,故④正确;
正确的是②③④这 个,
故选C.
第二部分
13.
【解析】把 代入 ,得 ,解得 .
14.
【解析】由题意,,即 .
15. ①②④
【解析】①根据图象可知,在 分钟,路程没有发生变化,所以小明中途休息的时间为 分钟,故正确;
②根据图象可知,当 时,,所以小明休息前爬山的平均速度为:(米/分钟),故正确;
③根据图象可知,小明在上述过程中所走的路程为 米,故错误;
④小明休息后的爬山的平均速度为:(米/分),
小明休息前爬山的平均速度为:(米/分钟),.
所以小明休息前爬山的平均速度大于休息后爬山的平均速度,故正确;
综上所述,正确的有①②④.
16.
17. ,,
18.
【解析】在坐标系中画出直线 及 , 两点,作 的中垂线,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 有 个交点;
以 为圆心、 长为半径画圆,与直线 也有 个交点,
故这样的点 共有 个.
第三部分
19. 正比例函数是 ,;
, 不是正比例函数.
20. (1) .
(2) 由题意得:,.
(3) 由题意得:,.
21. (1) ;
(2) 米;
(3) 小明会赢得比赛.
22. (1) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 ;
(2) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 ;
(3) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 ;
(4) 图略;与 轴的交点坐标为 ,与 轴的交点坐标为 .
23. (1)
(2)
【解析】令 ,
,
.
(3) 如图所示:
(4) ① 至
②答案不唯一,如 时, 随 的增大而增大
24. (1) ;
当在乙商场购买商品未超过 元 时,乙商场按照原价售卖,即 ;
当在乙商场购买物品超过 元时,超过部分按 折,
所以 ,化简得 ;
所以 ;.
(2) 由题意可知,当购买商品原价小于等于 时,甲商场打 折,乙商场不打折,所以甲商场购物更加划算;
当购买商品原价超过 元时,
若 ,即 此时甲商场花费更低,购物选择甲商场;
若 ,即 ,此时甲乙商场购物花费一样;
若 ,即 时,此时乙商场花费更低,购物选择乙商场;
综上所述:当购买商品原价金额小于 时,选择甲商场更划算;当购买商品原价金额等于 时,选择甲商场和乙商场购物一样划算;当购买商品原价金额大于 时,选择乙商场更划算.
25. (1) 通过画图观察可得当 时,.
(2) 如图所示.
(3)
【解析】在坐标系中画出直线 ,则三个图象中,两两图象交点的横坐标即为 为等腰三角形时线段 的长度,则 的长度约为 或 或 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
