人教版九年级上册数学 22.3实际问题与二次函数(图形运动问题)同步练习(含简单答案)
文档属性
| 名称 | 人教版九年级上册数学 22.3实际问题与二次函数(图形运动问题)同步练习(含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 632.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 07:01:07 | ||
图片预览

文档简介
人教版九年级上册数学22.3实际问题与二次函数(图形运动问题)同步练习
一、单选题
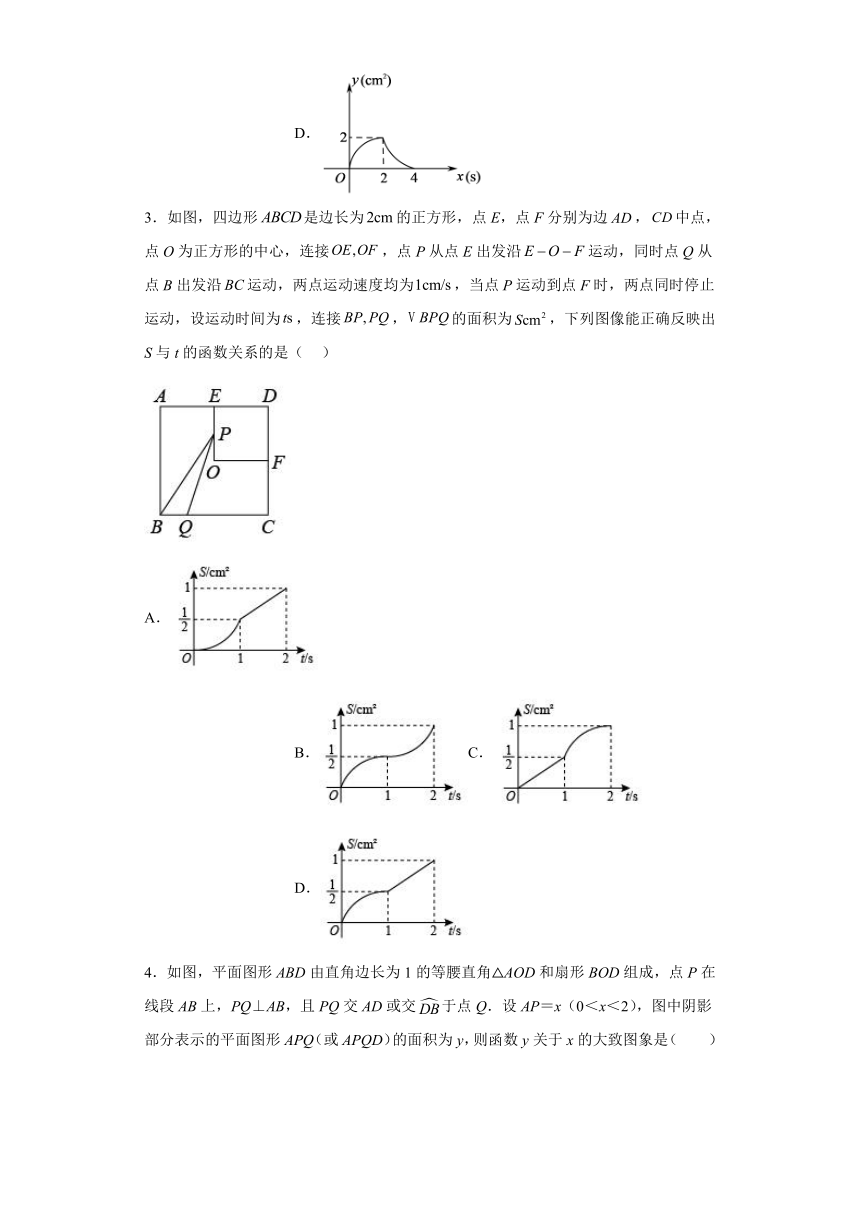
1.如图,是等腰直角三角形,,,为上的动点,交折线于点,设,的面积为,则与的函数图象正确的是( )
A. B.
C. D.
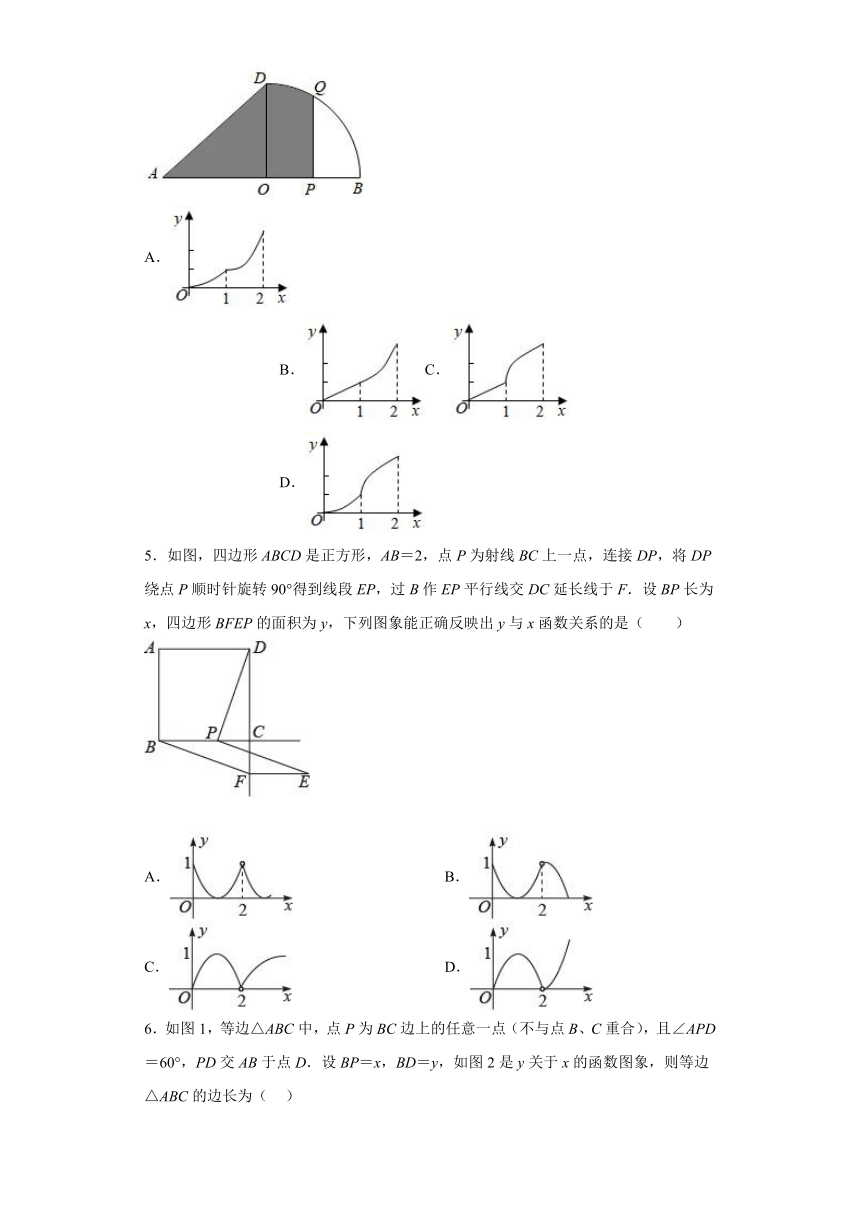
2.如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PO,设运动时间为xs,△APQ的面积为ycm2,则下列图像中能大致表示y与x的函数关系的是( )
A. B.C. D.
3.如图,四边形是边长为的正方形,点E,点F分别为边,中点,点O为正方形的中心,连接,点P从点E出发沿运动,同时点Q从点B出发沿运动,两点运动速度均为,当点P运动到点F时,两点同时停止运动,设运动时间为,连接,的面积为,下列图像能正确反映出S与t的函数关系的是( )
A. B.C. D.
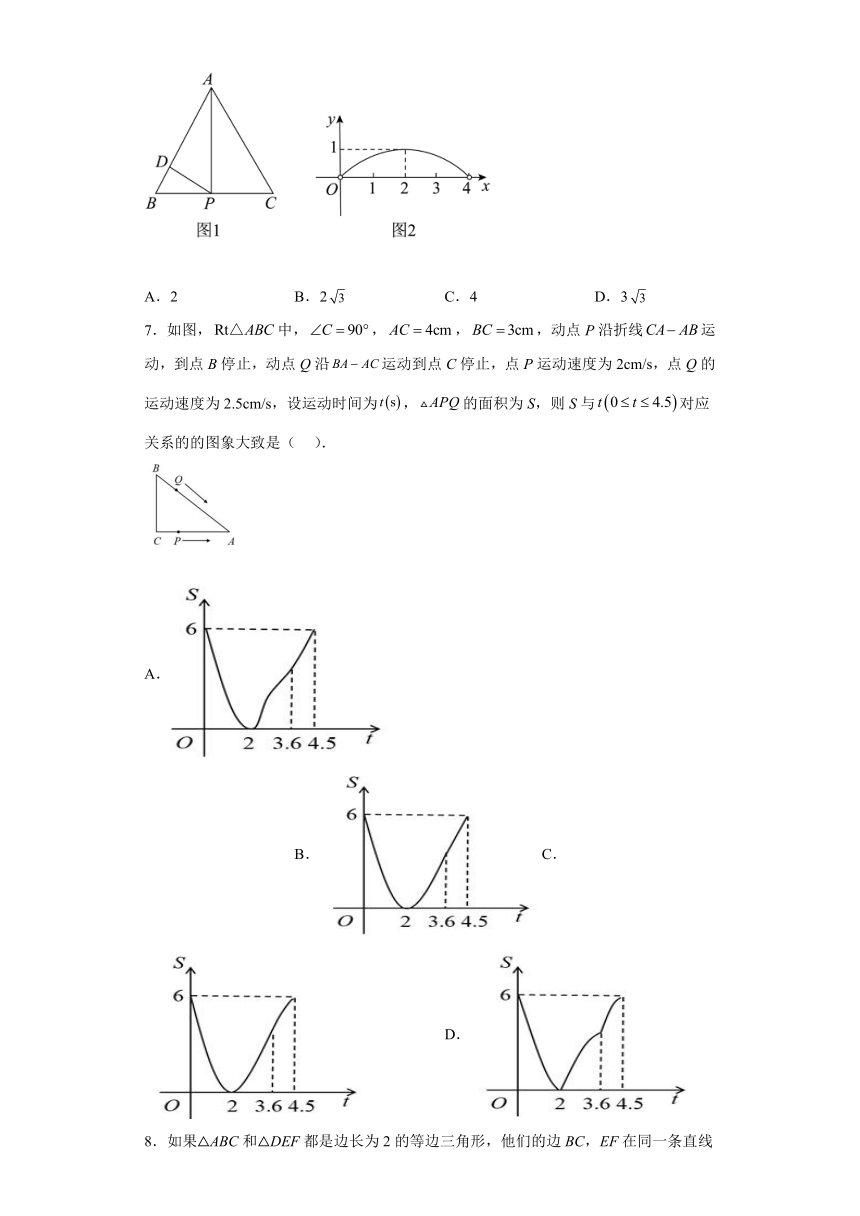
4.如图,平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成,点P在线段AB上,PQ⊥AB,且PQ交AD或交于点Q.设AP=x(0<x<2),图中阴影部分表示的平面图形APQ(或APQD)的面积为y,则函数y关于x的大致图象是( )
A. B.C. D.
5.如图,四边形ABCD是正方形,AB=2,点P为射线BC上一点,连接DP,将DP绕点P顺时针旋转90°得到线段EP,过B作EP平行线交DC延长线于F.设BP长为x,四边形BFEP的面积为y,下列图象能正确反映出y与x函数关系的是( )
A. B.
C. D.
6.如图1,等边△ABC中,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,如图2是y关于x的函数图象,则等边△ABC的边长为( )
A.2 B.2 C.4 D.3
7.如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的的图象大致是( ).
A. B.C. D.
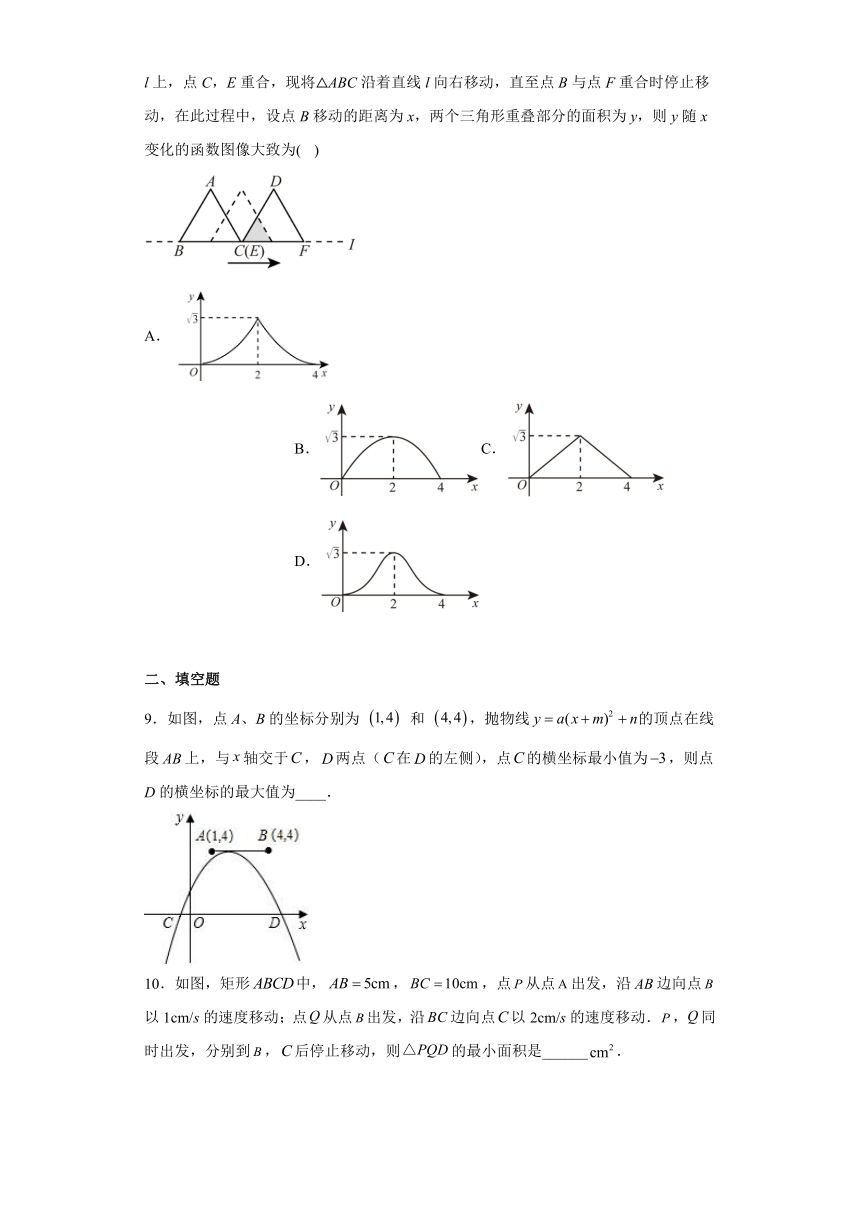
8.如果△ABC和△DEF都是边长为2的等边三角形,他们的边BC,EF在同一条直线l上,点C,E重合,现将△ABC沿着直线l向右移动,直至点B与点F重合时停止移动,在此过程中,设点B移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图像大致为( )
A. B.C. D.
二、填空题
9.如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
10.如图,矩形中,,,点从点出发,沿边向点以1cm/s的速度移动;点从点出发,沿边向点以2cm/s的速度移动.,同时出发,分别到,后停止移动,则的最小面积是______.
11.如图1,正方形ABCD中,点E为AB的中点,连接CE,动点P从A点出发,沿AB﹣BC﹣CD运动,同时,动点Q从A点出发,沿AD向点D运动,P,Q两点同时到达点D,设点P的运动时间为x(s),△APQ的面积为y(cm2),则y关于x的函数图象如图2,当△APQ与△CBE全等时,DP的长为 __________________cm.
12.如图,在中,,mm, mm,动点从点开始沿边向以1mm/s的速度移动(不与点重合),动点从点开始沿边向以2mm/s的速度移动(不与点重合).如果,分别从,同时出发,那么经过_______________________秒,四边形的面积最小.
13.二次函数y=2x2﹣4x+4的图象如图所示,其对称轴与它的图象交于点P,点N是其图象上异于点P的一点,若PM⊥y轴,MN⊥x轴,则=_____.
14.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4cm,动点P从点B出发沿射线BC方向以2cm/s的速度运动.设运动的时间为t秒,则当t=_____秒时,△ABP为直角三角形.
15.如图,在边长为的正方形中,点、、、分别从点、、、同时出发,均以的速度向点、、、匀速运动,当点到达点时,四个点同时停止运动,在运动过程中,当运动时间为_____时,四边形的面积最小,其最小值是_____.
16.如图,抛物线与轴的负半轴交于点,与轴交于点,连接,点分别是直线与抛物线上的点,若点围成的四边形是平行四边形,则点的坐标为__________.
三、解答题
17.如图1所示,为矩形的边上一点,动点同时从点出发,点沿折线运动到点时停止,点沿运动到点时停止,它们运动的速度都是秒.设同时出发秒时,的面积为,已知与的函数关系图象如图2所示.请回答:
(1)线段的长为_______cm;
(2)当运动时间秒时,之间的距离是_______.
18.将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设AP=x.
(1)当点Q在边CD上时,求证:PQ=PB.
(2)在(1)的情况下,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;
(3)当点P在线段AC上滑动时,当△PCQ是等腰三角形时,求x的值.
19.如图,已知抛物线与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式:
(2)求CED的面积S与D点运动时间t的函数解析式;当t为何值时,CED的面积最大?最大面积是多少?
20.如图,在Rt△ABC中,∠C=90°,AC=BC,AB=4cm,线段AB上一动点D,以1cm/s的速度从点A出发向终点B运动.过点D作DE⊥AB,交折线AC-CB于点E,以DE为一边,在DE右侧作正方形DEFC.设运动时间为x(s)(0<x<4).正方形DEFG与△ABC重叠部分面积为y(cm2).
(1)当x= s时,点F在BC上;
(2)求y关于x的函数解析式,并写出自变量x的取值范围.
参考答案:
1.B
2.A
3.D
4.D
5.D
6.C
7.B
8.A
9.8
10.
11.
12.4
13.2.
14.3或4
15. 3 18
16.或或
17. 5
18.(1)见解析
(2)
(3)0或1
19.(1)y=-x2+3x+8
(2)S=-t2+5t,当t=5时,CED的面积最大,最大面积是
20.(1)
(2)();();()
答案第2页,共2页
一、单选题
1.如图,是等腰直角三角形,,,为上的动点,交折线于点,设,的面积为,则与的函数图象正确的是( )
A. B.
C. D.
2.如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PO,设运动时间为xs,△APQ的面积为ycm2,则下列图像中能大致表示y与x的函数关系的是( )
A. B.C. D.
3.如图,四边形是边长为的正方形,点E,点F分别为边,中点,点O为正方形的中心,连接,点P从点E出发沿运动,同时点Q从点B出发沿运动,两点运动速度均为,当点P运动到点F时,两点同时停止运动,设运动时间为,连接,的面积为,下列图像能正确反映出S与t的函数关系的是( )
A. B.C. D.
4.如图,平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成,点P在线段AB上,PQ⊥AB,且PQ交AD或交于点Q.设AP=x(0<x<2),图中阴影部分表示的平面图形APQ(或APQD)的面积为y,则函数y关于x的大致图象是( )
A. B.C. D.
5.如图,四边形ABCD是正方形,AB=2,点P为射线BC上一点,连接DP,将DP绕点P顺时针旋转90°得到线段EP,过B作EP平行线交DC延长线于F.设BP长为x,四边形BFEP的面积为y,下列图象能正确反映出y与x函数关系的是( )
A. B.
C. D.
6.如图1,等边△ABC中,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,如图2是y关于x的函数图象,则等边△ABC的边长为( )
A.2 B.2 C.4 D.3
7.如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的的图象大致是( ).
A. B.C. D.
8.如果△ABC和△DEF都是边长为2的等边三角形,他们的边BC,EF在同一条直线l上,点C,E重合,现将△ABC沿着直线l向右移动,直至点B与点F重合时停止移动,在此过程中,设点B移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图像大致为( )
A. B.C. D.
二、填空题
9.如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
10.如图,矩形中,,,点从点出发,沿边向点以1cm/s的速度移动;点从点出发,沿边向点以2cm/s的速度移动.,同时出发,分别到,后停止移动,则的最小面积是______.
11.如图1,正方形ABCD中,点E为AB的中点,连接CE,动点P从A点出发,沿AB﹣BC﹣CD运动,同时,动点Q从A点出发,沿AD向点D运动,P,Q两点同时到达点D,设点P的运动时间为x(s),△APQ的面积为y(cm2),则y关于x的函数图象如图2,当△APQ与△CBE全等时,DP的长为 __________________cm.
12.如图,在中,,mm, mm,动点从点开始沿边向以1mm/s的速度移动(不与点重合),动点从点开始沿边向以2mm/s的速度移动(不与点重合).如果,分别从,同时出发,那么经过_______________________秒,四边形的面积最小.
13.二次函数y=2x2﹣4x+4的图象如图所示,其对称轴与它的图象交于点P,点N是其图象上异于点P的一点,若PM⊥y轴,MN⊥x轴,则=_____.
14.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=4cm,动点P从点B出发沿射线BC方向以2cm/s的速度运动.设运动的时间为t秒,则当t=_____秒时,△ABP为直角三角形.
15.如图,在边长为的正方形中,点、、、分别从点、、、同时出发,均以的速度向点、、、匀速运动,当点到达点时,四个点同时停止运动,在运动过程中,当运动时间为_____时,四边形的面积最小,其最小值是_____.
16.如图,抛物线与轴的负半轴交于点,与轴交于点,连接,点分别是直线与抛物线上的点,若点围成的四边形是平行四边形,则点的坐标为__________.
三、解答题
17.如图1所示,为矩形的边上一点,动点同时从点出发,点沿折线运动到点时停止,点沿运动到点时停止,它们运动的速度都是秒.设同时出发秒时,的面积为,已知与的函数关系图象如图2所示.请回答:
(1)线段的长为_______cm;
(2)当运动时间秒时,之间的距离是_______.
18.将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,设AP=x.
(1)当点Q在边CD上时,求证:PQ=PB.
(2)在(1)的情况下,设四边形PBCQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围;
(3)当点P在线段AC上滑动时,当△PCQ是等腰三角形时,求x的值.
19.如图,已知抛物线与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式:
(2)求CED的面积S与D点运动时间t的函数解析式;当t为何值时,CED的面积最大?最大面积是多少?
20.如图,在Rt△ABC中,∠C=90°,AC=BC,AB=4cm,线段AB上一动点D,以1cm/s的速度从点A出发向终点B运动.过点D作DE⊥AB,交折线AC-CB于点E,以DE为一边,在DE右侧作正方形DEFC.设运动时间为x(s)(0<x<4).正方形DEFG与△ABC重叠部分面积为y(cm2).
(1)当x= s时,点F在BC上;
(2)求y关于x的函数解析式,并写出自变量x的取值范围.
参考答案:
1.B
2.A
3.D
4.D
5.D
6.C
7.B
8.A
9.8
10.
11.
12.4
13.2.
14.3或4
15. 3 18
16.或或
17. 5
18.(1)见解析
(2)
(3)0或1
19.(1)y=-x2+3x+8
(2)S=-t2+5t,当t=5时,CED的面积最大,最大面积是
20.(1)
(2)();();()
答案第2页,共2页
同课章节目录
