11.2 实数(2) 课件(21张PPT)
文档属性
| 名称 | 11.2 实数(2) 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-19 08:46:09 | ||
图片预览








文档简介
(共21张PPT)
11.2 实数(2)
华师大版 八年级上册
教学目标
1.了解有理数的相反数、绝对值等概念、运算法则、运算律在实数范围内仍然适用.
2.能对实数进行大小比较和四则混合运算.
【教学重点】实数的性质、实数的大小比较及运算.
【教学难点】实数的大小比较.
复习回顾
问题1:用字母来表示有理数的加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律.
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
复习回顾
问题2:有理数的相反数是什么?不为0的数的倒数是什么?有理数的绝对值等于什么?
数a的相反数是-a(a表示任意一个有理数),一个正有理数的绝对值是它本身,一个负有利数的绝对值是它的相反数,0的绝对值是0.
这一法则能否推广到实数呢?
新知讲解
在七年级上学期学过的有关有理数的相反数和绝对值等概念、大小比较法则、运算法则以及运算律,对于实数也适用.
从有理数扩充到实数以后,正数总可以开方.在实数范围内,任意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.任意一个实数有且仅有一个立方根.
新知讲解
试一试:(1)分别写出 的相反数;
解: 的相反数是 ;π-3.14的的相反数是3.14-π.
(2)指出 分别是什么数的相反数.
解: 是 的相反数; 是 的相反数.
新知讲解
试一试:(3)求 的绝对值;
解:
(4)已知一个数的绝对值是 ,求这个数.
解:绝对值为 的数是 或 .
巩固练习
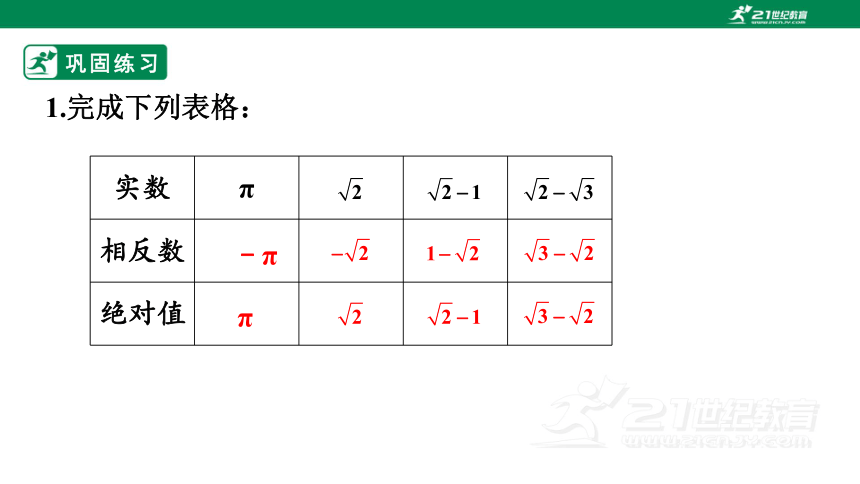
1.完成下列表格:
实数 π
相反数
绝对值
﹣π
π
例题讲解
涉及无理数的大小比较和运算,通常可以取它们的近似值来进行.
例1
试比较 与 π的大小.
解:用计算器求得
而π≈3.141592654,
因此
例题讲解
例2
计算: (精确到0.01)
解:
于是
取近似值计算时,中间结果通常应比要求的精确度多取一位.
例题讲解
例2
计算: (精确到0.01)
解:
于是
注:由于 ,所以
原式
由此算式,可直接将数据输入计算器进行计算.
巩固练习
2.比较下列各数的大小:
(1) 与 ;(2) 与 .
解:(1)因为 所以
(2)因为4>3,所以 所以
典例讲解
例3、计算:
巩固练习
3.计算: (精确到0.01)
解:原式
≈9×1.414-2×2.236-3×1.732
≈3.06
课堂总结
实数的性质及运算
性质:实数的相反数、绝对值、倒数运算.
实数的大小比较与运算
在实数范围内,有关有理数的相反数、倒数和绝对值等概念、大小比较、运算法则及运算律仍然适用.
拓展提高
1.将下列各数按从小到大的顺序排列,并用“<”号连接起来:
解: .
拓展提高
2.观察下列各方格图中阴影所示的图形(每一小方格的边长为1),如果它们都可以剪开,重新拼成正方形,那么所拼成的正方形的边长各为多少?这些正方形一样大吗?(如果你有兴趣,可以试试如何剪拼成一个正方形)
拓展提高
(1)
(2)
(3)
(4)
(5)
(6)
解:所拼成的正方形边长都为 ,这些正方形一样大.
拓展提高
3.(1)用计算器计算:
_________________;
__________________________;
_________________________________;
________________________________.
(2)观察题(1)中各式的计算结果,你能发现什么规律?
5
55
555
5555
(n为正整数)
(3)试运用发现的规律猜想下式的值,并通过计算器的计算验证你的猜想: _________________________.
55555
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2 实数(2)
华师大版 八年级上册
教学目标
1.了解有理数的相反数、绝对值等概念、运算法则、运算律在实数范围内仍然适用.
2.能对实数进行大小比较和四则混合运算.
【教学重点】实数的性质、实数的大小比较及运算.
【教学难点】实数的大小比较.
复习回顾
问题1:用字母来表示有理数的加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律.
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
复习回顾
问题2:有理数的相反数是什么?不为0的数的倒数是什么?有理数的绝对值等于什么?
数a的相反数是-a(a表示任意一个有理数),一个正有理数的绝对值是它本身,一个负有利数的绝对值是它的相反数,0的绝对值是0.
这一法则能否推广到实数呢?
新知讲解
在七年级上学期学过的有关有理数的相反数和绝对值等概念、大小比较法则、运算法则以及运算律,对于实数也适用.
从有理数扩充到实数以后,正数总可以开方.在实数范围内,任意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.任意一个实数有且仅有一个立方根.
新知讲解
试一试:(1)分别写出 的相反数;
解: 的相反数是 ;π-3.14的的相反数是3.14-π.
(2)指出 分别是什么数的相反数.
解: 是 的相反数; 是 的相反数.
新知讲解
试一试:(3)求 的绝对值;
解:
(4)已知一个数的绝对值是 ,求这个数.
解:绝对值为 的数是 或 .
巩固练习
1.完成下列表格:
实数 π
相反数
绝对值
﹣π
π
例题讲解
涉及无理数的大小比较和运算,通常可以取它们的近似值来进行.
例1
试比较 与 π的大小.
解:用计算器求得
而π≈3.141592654,
因此
例题讲解
例2
计算: (精确到0.01)
解:
于是
取近似值计算时,中间结果通常应比要求的精确度多取一位.
例题讲解
例2
计算: (精确到0.01)
解:
于是
注:由于 ,所以
原式
由此算式,可直接将数据输入计算器进行计算.
巩固练习
2.比较下列各数的大小:
(1) 与 ;(2) 与 .
解:(1)因为 所以
(2)因为4>3,所以 所以
典例讲解
例3、计算:
巩固练习
3.计算: (精确到0.01)
解:原式
≈9×1.414-2×2.236-3×1.732
≈3.06
课堂总结
实数的性质及运算
性质:实数的相反数、绝对值、倒数运算.
实数的大小比较与运算
在实数范围内,有关有理数的相反数、倒数和绝对值等概念、大小比较、运算法则及运算律仍然适用.
拓展提高
1.将下列各数按从小到大的顺序排列,并用“<”号连接起来:
解: .
拓展提高
2.观察下列各方格图中阴影所示的图形(每一小方格的边长为1),如果它们都可以剪开,重新拼成正方形,那么所拼成的正方形的边长各为多少?这些正方形一样大吗?(如果你有兴趣,可以试试如何剪拼成一个正方形)
拓展提高
(1)
(2)
(3)
(4)
(5)
(6)
解:所拼成的正方形边长都为 ,这些正方形一样大.
拓展提高
3.(1)用计算器计算:
_________________;
__________________________;
_________________________________;
________________________________.
(2)观察题(1)中各式的计算结果,你能发现什么规律?
5
55
555
5555
(n为正整数)
(3)试运用发现的规律猜想下式的值,并通过计算器的计算验证你的猜想: _________________________.
55555
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
