2022-2023学年苏科版九年级数学上册1.4用一元二次方程解决问题 强化提优训练(含答案)
文档属性
| 名称 | 2022-2023学年苏科版九年级数学上册1.4用一元二次方程解决问题 强化提优训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 466.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 07:47:06 | ||
图片预览



文档简介
2022-2023学年苏科版九年级数学上《1.4用一元二次方程解决问题》强化提优训练(二)
(时间:90分钟 满分:120分)
一.选择题(30分)
1. 平面上不重合的两点确定一条直线,不同的三点最多可确定3条直线. 若平面上不同的n个点最多可确定21条直线,则n的值为( )
A. 5 B. 6 C. 7 D. 8
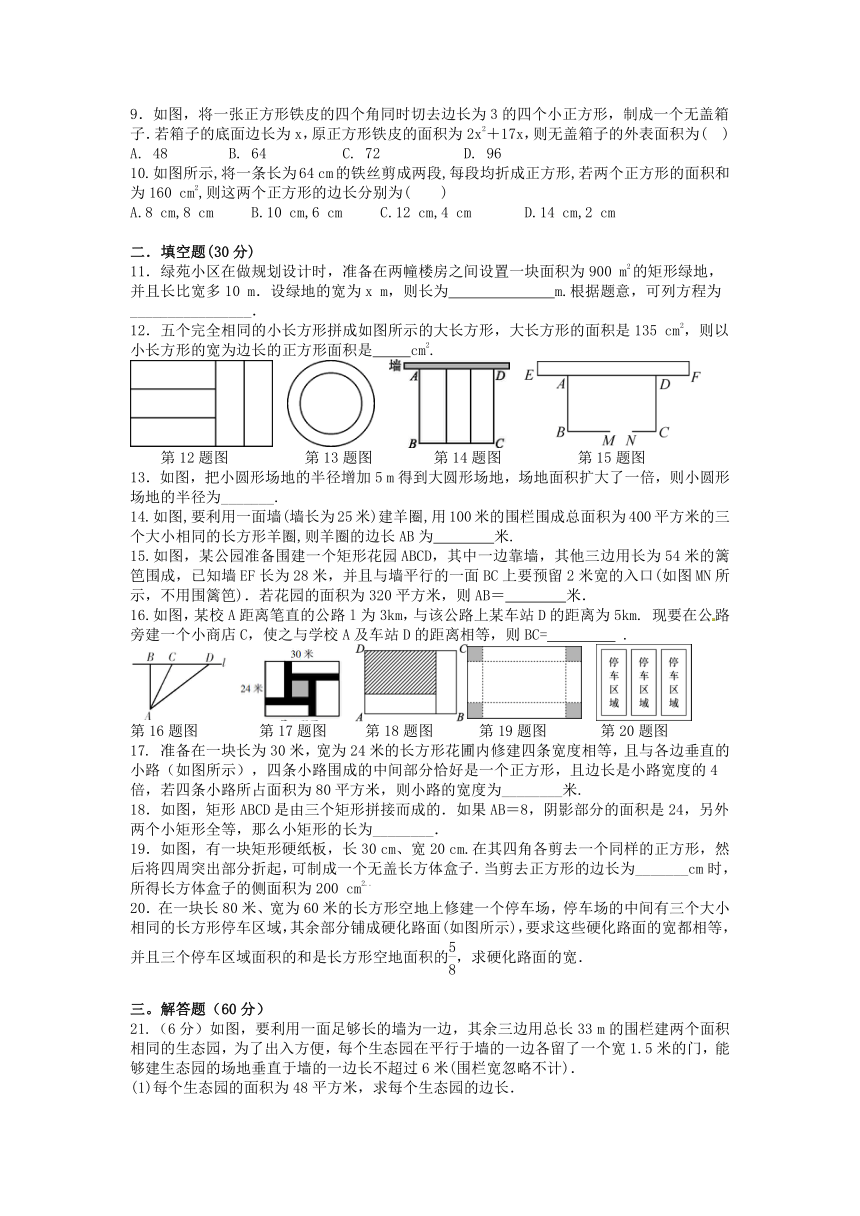
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长. 设原正方形的空地的边长为xm,则可列方程为( )
A. (x+1)(x+2)=18 B. x2-3x+16=0 C. (x-1)(x-2)=18 D. x2+3x+16=0
第2题图 第3题图 第4题图 第5题图
3. 如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
4. 如图,将一张正方形铁皮的四个角同时切去边长为2的四个小正方形,制成一个无盖箱子,若箱子的底面边长为x,原正方形铁皮的面积为x2+24x,则无盖箱子的外表面积为( )
A. 1 B. 4 C. 6 D. 9
5.如图,某中学有一块长30 m、宽20 m的长方形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x(m),则可列方程为( )
A. (30-x)(20-x)=×20×30 B. (30-2x)(20-x)=×20×30
C. 30x+2×20x=×20×30 D. (30-2x)(20-x)=×20×30
6.如图,在长为60 m、宽为40 m的长方形场地上修建1横2纵三条宽度相等的甬道,其余部分为绿地.若绿化面积为长方形面积的一半,则甬道的宽应为多少米?设甬道的宽为x(m),则列出的方程错误的是( )
A. (60-2x)(40-x)=×40×60 B. 40×60-40×2x-60x+2x2=×40×60
C. 40×2x+60x-2x2=×40×60 D. (60-x)(40-2x)=×40×60
第6题图 第8题图 第9题图 第10题图
7.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A. x2-6=(10-x)2 B. x2-62=(10-x)2 C. x2+6=(10-x)2 D. x2+62=(10-x)2
8.如图所示为两条互相垂直的街道,且A到B,C的距离都是7 km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4 km/h,则两人之间的距离为5 km时是出发后( )
A. 1 h B. 0.75 h C. 1.2 h或0.75 h D. 1 h或0.75
9.如图,将一张正方形铁皮的四个角同时切去边长为3的四个小正方形,制成一个无盖箱子.若箱子的底面边长为x,原正方形铁皮的面积为2x2+17x,则无盖箱子的外表面积为( )
A. 48 B. 64 C. 72 D. 96
10.如图所示,将一条长为64 cm的铁丝剪成两段,每段均折成正方形,若两个正方形的面积和为160 cm2,则这两个正方形的边长分别为( )
A.8 cm,8 cm B.10 cm,6 cm C.12 cm,4 cm D.14 cm,2 cm
二.填空题(30分)
11.绿苑小区在做规划设计时,准备在两幢楼房之间设置一块面积为900 m2的矩形绿地,并且长比宽多10 m.设绿地的宽为x m,则长为 m.根据题意,可列方程为________________.
12.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的面积是135 cm2,则以小长方形的宽为边长的正方形面积是 cm2.
第12题图 第13题图 第14题图 第15题图
13.如图,把小圆形场地的半径增加5 m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为_______.
14.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的长方形羊圈,则羊圈的边长AB为 米.
15.如图,某公园准备围建一个矩形花园ABCD,其中一边靠墙,其他三边用长为54米的篱笆围成,已知墙EF长为28米,并且与墙平行的一面BC上要预留2米宽的入口(如图MN所示,不用围篱笆).若花园的面积为320平方米,则AB= 米.
16.如图,某校A距离笔直的公路l为3km,与该公路上某车站D的距离为5km. 现要在公路旁建一个小商店C,使之与学校A及车站D的距离相等,则BC= .
第16题图 第17题图 第18题图 第19题图 第20题图
17. 准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路(如图所示),四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为________米.
18.如图,矩形ABCD是由三个矩形拼接而成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为________.
19.如图,有一块矩形硬纸板,长30 cm、宽20 cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长为_______cm时,所得长方体盒子的侧面积为200 cm2..
20.在一块长80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面(如图所示),要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的,求硬化路面的宽.
三。解答题(60分)
21.(6分)如图,要利用一面足够长的墙为一边,其余三边用总长33 m的围栏建两个面积相同的生态园,为了出入方便,每个生态园在平行于墙的一边各留了一个宽1.5米的门,能够建生态园的场地垂直于墙的一边长不超过6米(围栏宽忽略不计).
(1)每个生态园的面积为48平方米,求每个生态园的边长.
(2)每个生态园的面积 (填“能”或“不能”)达到108平方米.
22.(8分)如图,有一段19 m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用36 m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160 m2的长方形场地?
(2)长方形场地的面积能达到170 m2吗?如果能,请给出设计方案;如果不能,请说明理由.
23.(8分)某商店以20元/千克的价格购进一批商品,经调查发现,在一段时间内,销售量y(kg)与销售单价x(元)之间为一次函数关系,如图所示.
(1)求一次函数的表达式.
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
24.(8分)如图,在△ABC中,AB=6 cm,BC=4 cm,∠B=60°,动点P,Q分别从点A,B同时出发,分别沿AB,BC方向匀速移动,点P,Q的速度分别为2 cm/s和1 cm/s.当点P到达点B时,P,Q两点同时停止运动.设点P的运动时间为t(s),当t=或时,△PBQ是直角三角形.
25.(8分)如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q为顶点的三角形是等腰三角形?
26.(10分)如图,在长方形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿边AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空:BQ= cm,PB=______cm(用含 t的代数式表示).
(2)当t为何值时,PQ的长度等于5 cm
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.
27.(12分)如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.
(1)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.若点P,Q分别从点A,B同时出发,则经过几秒后,△PBQ的面积等于8 cm2
(2)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点P从点A出发,沿射线AB方向以1 cm/s的速度移动,点Q从点C出发,沿射线CB方向以2 cm/s的速度移动,点P,Q同时出发.问:经过几秒后,△PBQ的面积为1 cm2
教师样卷
一.选择题(30分)
1. 平面上不重合的两点确定一条直线,不同的三点最多可确定3条直线. 若平面上不同的n个点最多可确定21条直线,则n的值为( C )
A. 5 B. 6 C. 7 D. 8
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长. 设原正方形的空地的边长为xm,则可列方程为( C )
A. (x+1)(x+2)=18 B. x2-3x+16=0 C. (x-1)(x-2)=18 D. x2+3x+16=0
第2题图 第3题图 第4题图 第5题图
3. 如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( B )
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
4. 如图,将一张正方形铁皮的四个角同时切去边长为2的四个小正方形,制成一个无盖箱子,若箱子的底面边长为x,原正方形铁皮的面积为x2+24x,则无盖箱子的外表面积为( D )
A. 1 B. 4 C. 6 D. 9
5.如图,某中学有一块长30 m、宽20 m的长方形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x(m),则可列方程为(D)
A. (30-x)(20-x)=×20×30 B. (30-2x)(20-x)=×20×30
C. 30x+2×20x=×20×30 D. (30-2x)(20-x)=×20×30
6.如图,在长为60 m、宽为40 m的长方形场地上修建1横2纵三条宽度相等的甬道,其余部分为绿地.若绿化面积为长方形面积的一半,则甬道的宽应为多少米?设甬道的宽为x(m),则列出的方程错误的是(D)
A. (60-2x)(40-x)=×40×60 B. 40×60-40×2x-60x+2x2=×40×60
C. 40×2x+60x-2x2=×40×60 D. (60-x)(40-2x)=×40×60
第6题图 第8题图 第9题图 第10题图
7.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为(D)
A. x2-6=(10-x)2 B. x2-62=(10-x)2 C. x2+6=(10-x)2 D. x2+62=(10-x)2
8.如图所示为两条互相垂直的街道,且A到B,C的距离都是7 km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4 km/h,则两人之间的距离为5 km时是出发后(D)
A. 1 h B. 0.75 h C. 1.2 h或0.75 h D. 1 h或0.75
9.如图,将一张正方形铁皮的四个角同时切去边长为3的四个小正方形,制成一个无盖箱子.若箱子的底面边长为x,原正方形铁皮的面积为2x2+17x,则无盖箱子的外表面积为(B)
A. 48 B. 64 C. 72 D. 96
10.如图所示,将一条长为64 cm的铁丝剪成两段,每段均折成正方形,若两个正方形的面积和为160 cm2,则这两个正方形的边长分别为( C )
A.8 cm,8 cm B.10 cm,6 cm C.12 cm,4 cm D.14 cm,2 cm
二.填空题(30分)
11.绿苑小区在做规划设计时,准备在两幢楼房之间设置一块面积为900 m2的矩形绿地,并且长比宽多10 m.设绿地的宽为x m,则长为 m.根据题意,可列方程为________________.
【答案】(x+10) x(x+10)=900
12.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的面积是135 cm2,则以小长方形的宽为边长的正方形面积是 cm2.
【答案】9
第12题图 第13题图 第14题图 第15题图
13.如图,把小圆形场地的半径增加5 m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为_______.
【答案】(5+5)m
14.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的长方形羊圈,则羊圈的边长AB为 米.
【答案】20
15.如图,某公园准备围建一个矩形花园ABCD,其中一边靠墙,其他三边用长为54米的篱笆围成,已知墙EF长为28米,并且与墙平行的一面BC上要预留2米宽的入口(如图MN所示,不用围篱笆).若花园的面积为320平方米,则AB= 米.
【答案】20
16.如图,某校A距离笔直的公路l为3km,与该公路上某车站D的距离为5km. 现要在公路旁建一个小商店C,使之与学校A及车站D的距离相等,则BC= .
【答案】km
第16题图 第17题图 第18题图 第19题图 第20题图
17. 准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路(如图所示),四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为________米.
【答案】
18.如图,矩形ABCD是由三个矩形拼接而成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为________.
【答案】6
19.如图,有一块矩形硬纸板,长30 cm、宽20 cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长为_______cm时,所得长方体盒子的侧面积为200 cm2..
【答案】
20.在一块长80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面(如图所示),要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的,求硬化路面的宽.
【答案】5 解:设硬化路面的宽为x米,依题意,得(80-4x)(60-2x)=×80×60.解得x1=5,x2=45.当x=5时,80-4x=80-4×5=60>0,符合题意;当x=45时,80-4x=80-4×45=-100<0,不符合题意,舍去.
三。解答题(60分)
21.(6分)如图,要利用一面足够长的墙为一边,其余三边用总长33 m的围栏建两个面积相同的生态园,为了出入方便,每个生态园在平行于墙的一边各留了一个宽1.5米的门,能够建生态园的场地垂直于墙的一边长不超过6米(围栏宽忽略不计).
(1)每个生态园的面积为48平方米,求每个生态园的边长.
(2)每个生态园的面积 不能 (填“能”或“不能”)达到108平方米.
解:(1)设每个生态园垂直于墙的边长为x米,根据题意,得x(33+1.5×2-3x)=48×2.解得x1=4,x2=8>6(不合题意,舍去).当x=4时,33+1.5×2-3x=24,24÷2=12.
答:每个生态园垂直于墙的边长为4米,平行于墙的边长为12米.
22.(8分)如图,有一段19 m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用36 m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160 m2的长方形场地?
(2)长方形场地的面积能达到170 m2吗?如果能,请给出设计方案;如果不能,请说明理由.
解: (1)设CD=x(m),则DE=(36-2x)m.由题意,得x(36-2x)=160.整理,得x2-18x+80=0,解得x1=10,x2=8.当x1=10时,36-2x=16<19,符合题意;当x2=8时,36-2x=20>19,不合题意,舍去.∴CD=FE=10 m,DE=16 m.
(2)不能.理由如下:设CD=y(m),则DE=(36-2y)m.由题意,得y(36-2y)=170,整理,得y2-18y+85=0.∵Δ=(-18)2-4×1×85=-16<0,∴方程没有实数根,
∴长方形场地的面积不能达到170 m2.
23.(8分)某商店以20元/千克的价格购进一批商品,经调查发现,在一段时间内,销售量y(kg)与销售单价x(元)之间为一次函数关系,如图所示.
(1)求一次函数的表达式.
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
解: (1)设y关于x的函数表达式为y=kx+b,把点(20,60),(80,0)的坐标代入,得
解得∴y关于x的函数表达式为y=-x+80(20<x≤80).
(2)由题意,得(x-20)(-x+80)=800,解得x1=40,x2=60.答:销售单价应定为每千克40元或60元.
24.(8分)如图,在△ABC中,AB=6 cm,BC=4 cm,∠B=60°,动点P,Q分别从点A,B同时出发,分别沿AB,BC方向匀速移动,点P,Q的速度分别为2 cm/s和1 cm/s.当点P到达点B时,P,Q两点同时停止运动.设点P的运动时间为t(s),当t=或时,△PBQ是直角三角形.
解:由题意,得∴0①当∠BQP=90°时,∵∠B=60°,∴∠BPQ=90°-60°=30°,∴BQ=BP,即t=(6-2t),解得t=. ②当∠BPQ=90°时,∵∠B=60°,∴∠BQP=90°-60°=30°∴BP=BQ,即6-2t=t,解得t=.综上所述,当t=或时,△PBQ是直角三角形.
25.(8分)如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q为顶点的三角形是等腰三角形?
解:过点P作PM⊥BC于点M,则四边形PMCD为长方形,∴PM=CD=12,CM=PD=2t,CQ=t,∴QM=t,BQ=16-t,BM=16-2t.易得PD=2t≤21,∴t≤10.5.
①当PQ=BQ时,在Rt△PMQ中,PQ2=PM2+QM2=122+t2,由PQ2=BQ2,得122+t2=(16-t)2,解得t=. ②当BP=BQ时,在Rt△PMB中,BP2=BM2+PM2=(16-2t)2+122,
由BP2=BQ2,得(16-2t)2+122=(16-t)2,即3t2-32t+144=0.∵b2-4ac=-704<0,
∴3t2-32t+144=0无实数根,∴BP≠BQ.③当BP=PQ时,∵PM⊥BQ,∴BM=QM,
∴16-2t=t,解得t=.综上所述,当t=或 时,以B,P,Q为顶点的三角形是等腰三角形.
26.(10分)如图,在长方形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿边AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空:BQ= 2t cm,PB=(5-t)cm(用含 t的代数式表示).
(2)当t为何值时,PQ的长度等于5 cm
解:由题意,得(5-t)2+(2t)2=52,解得t1=0,t2=2.故当t=0或2时,PQ的长度等于5 cm.
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.
解:存在,当t=1时,能够使得五边形APQCD的面积等于26 cm2.理由如下:
长方形ABCD的面积是5×6=30(cm2),则△PBQ的面积为30-26=4(cm2).
依题意,得(5-t)×2t×=4,解得t1=4,t2=1.当t=4时,2t=8>6,故t=4不符合题意,舍去.故当t=1时,五边形APQCD的面积等于26 cm2.
27.(12分)如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.
(1)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.若点P,Q分别从点A,B同时出发,则经过几秒后,△PBQ的面积等于8 cm2
(2)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点P从点A出发,沿射线AB方向以1 cm/s的速度移动,点Q从点C出发,沿射线CB方向以2 cm/s的速度移动,点P,Q同时出发.问:经过几秒后,△PBQ的面积为1 cm2
【解】 (1)设经过x(s)后,△PBQ的面积等于8 cm2,由题意,得(6-x)·2x=8,解得x1=2,x2=4.经检验,x1,x2均符合题意,故经过2 s或4 s后,△PBQ的面积等于8 cm2.(2)不能.理由如下:设经过y(s),线段PQ将△ABC分成面积相等的两部分,由题意,得S△ABC=×6×8=24(cm2),∴(6-y)·2y=12,∴y2-6y+12=0.∵Δ=b2-4ac=36-4×12=-12<0,∴此方程无实数根,∴线段PQ不能将△ABC分成面积相等的两部分.
(3)由题意得,在6 s内,点P在线段AB上,超过6 s,点P在线段AB的延长线上;
在4 s内,点Q在线段CB上,超过4 s,点Q在线段CB的延长线上.
分三种情况讨论:①当点P在线段AB上,点Q在线段CB上,即运动时间不超过4 s时,
设经过m(s)后,△PBQ的面积为1 cm2,由题意,得(6-m)(8-2m)=1,解得m1=5+(不合题意,舍去),m2=5-.②当点P在线段AB上,点Q在射线CB上,即运动时间超过4 s,不超过6 s时,设经过n(s)后,△PBQ的面积为1 cm2,由题意,得(6-n)(2n-8)=1,
解得n1=n2=5.③当点P在射线AB上,点Q在射线CB上,即运动时间超过6 s时,
设经过k(s)后,△PBQ的面积为1 cm2,由题意,得(k-6)(2k-8)=1,解得k1=5+,k2=5-(不合题意,舍去).综上所述,经过(5-)s或5 s或(5+)s后,△PBQ的面积为1 cm2.
(时间:90分钟 满分:120分)
一.选择题(30分)
1. 平面上不重合的两点确定一条直线,不同的三点最多可确定3条直线. 若平面上不同的n个点最多可确定21条直线,则n的值为( )
A. 5 B. 6 C. 7 D. 8
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长. 设原正方形的空地的边长为xm,则可列方程为( )
A. (x+1)(x+2)=18 B. x2-3x+16=0 C. (x-1)(x-2)=18 D. x2+3x+16=0
第2题图 第3题图 第4题图 第5题图
3. 如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
4. 如图,将一张正方形铁皮的四个角同时切去边长为2的四个小正方形,制成一个无盖箱子,若箱子的底面边长为x,原正方形铁皮的面积为x2+24x,则无盖箱子的外表面积为( )
A. 1 B. 4 C. 6 D. 9
5.如图,某中学有一块长30 m、宽20 m的长方形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x(m),则可列方程为( )
A. (30-x)(20-x)=×20×30 B. (30-2x)(20-x)=×20×30
C. 30x+2×20x=×20×30 D. (30-2x)(20-x)=×20×30
6.如图,在长为60 m、宽为40 m的长方形场地上修建1横2纵三条宽度相等的甬道,其余部分为绿地.若绿化面积为长方形面积的一半,则甬道的宽应为多少米?设甬道的宽为x(m),则列出的方程错误的是( )
A. (60-2x)(40-x)=×40×60 B. 40×60-40×2x-60x+2x2=×40×60
C. 40×2x+60x-2x2=×40×60 D. (60-x)(40-2x)=×40×60
第6题图 第8题图 第9题图 第10题图
7.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A. x2-6=(10-x)2 B. x2-62=(10-x)2 C. x2+6=(10-x)2 D. x2+62=(10-x)2
8.如图所示为两条互相垂直的街道,且A到B,C的距离都是7 km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4 km/h,则两人之间的距离为5 km时是出发后( )
A. 1 h B. 0.75 h C. 1.2 h或0.75 h D. 1 h或0.75
9.如图,将一张正方形铁皮的四个角同时切去边长为3的四个小正方形,制成一个无盖箱子.若箱子的底面边长为x,原正方形铁皮的面积为2x2+17x,则无盖箱子的外表面积为( )
A. 48 B. 64 C. 72 D. 96
10.如图所示,将一条长为64 cm的铁丝剪成两段,每段均折成正方形,若两个正方形的面积和为160 cm2,则这两个正方形的边长分别为( )
A.8 cm,8 cm B.10 cm,6 cm C.12 cm,4 cm D.14 cm,2 cm
二.填空题(30分)
11.绿苑小区在做规划设计时,准备在两幢楼房之间设置一块面积为900 m2的矩形绿地,并且长比宽多10 m.设绿地的宽为x m,则长为 m.根据题意,可列方程为________________.
12.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的面积是135 cm2,则以小长方形的宽为边长的正方形面积是 cm2.
第12题图 第13题图 第14题图 第15题图
13.如图,把小圆形场地的半径增加5 m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为_______.
14.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的长方形羊圈,则羊圈的边长AB为 米.
15.如图,某公园准备围建一个矩形花园ABCD,其中一边靠墙,其他三边用长为54米的篱笆围成,已知墙EF长为28米,并且与墙平行的一面BC上要预留2米宽的入口(如图MN所示,不用围篱笆).若花园的面积为320平方米,则AB= 米.
16.如图,某校A距离笔直的公路l为3km,与该公路上某车站D的距离为5km. 现要在公路旁建一个小商店C,使之与学校A及车站D的距离相等,则BC= .
第16题图 第17题图 第18题图 第19题图 第20题图
17. 准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路(如图所示),四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为________米.
18.如图,矩形ABCD是由三个矩形拼接而成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为________.
19.如图,有一块矩形硬纸板,长30 cm、宽20 cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长为_______cm时,所得长方体盒子的侧面积为200 cm2..
20.在一块长80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面(如图所示),要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的,求硬化路面的宽.
三。解答题(60分)
21.(6分)如图,要利用一面足够长的墙为一边,其余三边用总长33 m的围栏建两个面积相同的生态园,为了出入方便,每个生态园在平行于墙的一边各留了一个宽1.5米的门,能够建生态园的场地垂直于墙的一边长不超过6米(围栏宽忽略不计).
(1)每个生态园的面积为48平方米,求每个生态园的边长.
(2)每个生态园的面积 (填“能”或“不能”)达到108平方米.
22.(8分)如图,有一段19 m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用36 m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160 m2的长方形场地?
(2)长方形场地的面积能达到170 m2吗?如果能,请给出设计方案;如果不能,请说明理由.
23.(8分)某商店以20元/千克的价格购进一批商品,经调查发现,在一段时间内,销售量y(kg)与销售单价x(元)之间为一次函数关系,如图所示.
(1)求一次函数的表达式.
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
24.(8分)如图,在△ABC中,AB=6 cm,BC=4 cm,∠B=60°,动点P,Q分别从点A,B同时出发,分别沿AB,BC方向匀速移动,点P,Q的速度分别为2 cm/s和1 cm/s.当点P到达点B时,P,Q两点同时停止运动.设点P的运动时间为t(s),当t=或时,△PBQ是直角三角形.
25.(8分)如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q为顶点的三角形是等腰三角形?
26.(10分)如图,在长方形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿边AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空:BQ= cm,PB=______cm(用含 t的代数式表示).
(2)当t为何值时,PQ的长度等于5 cm
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.
27.(12分)如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.
(1)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.若点P,Q分别从点A,B同时出发,则经过几秒后,△PBQ的面积等于8 cm2
(2)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点P从点A出发,沿射线AB方向以1 cm/s的速度移动,点Q从点C出发,沿射线CB方向以2 cm/s的速度移动,点P,Q同时出发.问:经过几秒后,△PBQ的面积为1 cm2
教师样卷
一.选择题(30分)
1. 平面上不重合的两点确定一条直线,不同的三点最多可确定3条直线. 若平面上不同的n个点最多可确定21条直线,则n的值为( C )
A. 5 B. 6 C. 7 D. 8
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长. 设原正方形的空地的边长为xm,则可列方程为( C )
A. (x+1)(x+2)=18 B. x2-3x+16=0 C. (x-1)(x-2)=18 D. x2+3x+16=0
第2题图 第3题图 第4题图 第5题图
3. 如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( B )
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
4. 如图,将一张正方形铁皮的四个角同时切去边长为2的四个小正方形,制成一个无盖箱子,若箱子的底面边长为x,原正方形铁皮的面积为x2+24x,则无盖箱子的外表面积为( D )
A. 1 B. 4 C. 6 D. 9
5.如图,某中学有一块长30 m、宽20 m的长方形空地,计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图所示,求花带的宽度.设花带的宽度为x(m),则可列方程为(D)
A. (30-x)(20-x)=×20×30 B. (30-2x)(20-x)=×20×30
C. 30x+2×20x=×20×30 D. (30-2x)(20-x)=×20×30
6.如图,在长为60 m、宽为40 m的长方形场地上修建1横2纵三条宽度相等的甬道,其余部分为绿地.若绿化面积为长方形面积的一半,则甬道的宽应为多少米?设甬道的宽为x(m),则列出的方程错误的是(D)
A. (60-2x)(40-x)=×40×60 B. 40×60-40×2x-60x+2x2=×40×60
C. 40×2x+60x-2x2=×40×60 D. (60-x)(40-2x)=×40×60
第6题图 第8题图 第9题图 第10题图
7.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为(D)
A. x2-6=(10-x)2 B. x2-62=(10-x)2 C. x2+6=(10-x)2 D. x2+62=(10-x)2
8.如图所示为两条互相垂直的街道,且A到B,C的距离都是7 km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4 km/h,则两人之间的距离为5 km时是出发后(D)
A. 1 h B. 0.75 h C. 1.2 h或0.75 h D. 1 h或0.75
9.如图,将一张正方形铁皮的四个角同时切去边长为3的四个小正方形,制成一个无盖箱子.若箱子的底面边长为x,原正方形铁皮的面积为2x2+17x,则无盖箱子的外表面积为(B)
A. 48 B. 64 C. 72 D. 96
10.如图所示,将一条长为64 cm的铁丝剪成两段,每段均折成正方形,若两个正方形的面积和为160 cm2,则这两个正方形的边长分别为( C )
A.8 cm,8 cm B.10 cm,6 cm C.12 cm,4 cm D.14 cm,2 cm
二.填空题(30分)
11.绿苑小区在做规划设计时,准备在两幢楼房之间设置一块面积为900 m2的矩形绿地,并且长比宽多10 m.设绿地的宽为x m,则长为 m.根据题意,可列方程为________________.
【答案】(x+10) x(x+10)=900
12.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的面积是135 cm2,则以小长方形的宽为边长的正方形面积是 cm2.
【答案】9
第12题图 第13题图 第14题图 第15题图
13.如图,把小圆形场地的半径增加5 m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为_______.
【答案】(5+5)m
14.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的长方形羊圈,则羊圈的边长AB为 米.
【答案】20
15.如图,某公园准备围建一个矩形花园ABCD,其中一边靠墙,其他三边用长为54米的篱笆围成,已知墙EF长为28米,并且与墙平行的一面BC上要预留2米宽的入口(如图MN所示,不用围篱笆).若花园的面积为320平方米,则AB= 米.
【答案】20
16.如图,某校A距离笔直的公路l为3km,与该公路上某车站D的距离为5km. 现要在公路旁建一个小商店C,使之与学校A及车站D的距离相等,则BC= .
【答案】km
第16题图 第17题图 第18题图 第19题图 第20题图
17. 准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路(如图所示),四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为________米.
【答案】
18.如图,矩形ABCD是由三个矩形拼接而成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为________.
【答案】6
19.如图,有一块矩形硬纸板,长30 cm、宽20 cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长为_______cm时,所得长方体盒子的侧面积为200 cm2..
【答案】
20.在一块长80米、宽为60米的长方形空地上修建一个停车场,停车场的中间有三个大小相同的长方形停车区域,其余部分铺成硬化路面(如图所示),要求这些硬化路面的宽都相等,并且三个停车区域面积的和是长方形空地面积的,求硬化路面的宽.
【答案】5 解:设硬化路面的宽为x米,依题意,得(80-4x)(60-2x)=×80×60.解得x1=5,x2=45.当x=5时,80-4x=80-4×5=60>0,符合题意;当x=45时,80-4x=80-4×45=-100<0,不符合题意,舍去.
三。解答题(60分)
21.(6分)如图,要利用一面足够长的墙为一边,其余三边用总长33 m的围栏建两个面积相同的生态园,为了出入方便,每个生态园在平行于墙的一边各留了一个宽1.5米的门,能够建生态园的场地垂直于墙的一边长不超过6米(围栏宽忽略不计).
(1)每个生态园的面积为48平方米,求每个生态园的边长.
(2)每个生态园的面积 不能 (填“能”或“不能”)达到108平方米.
解:(1)设每个生态园垂直于墙的边长为x米,根据题意,得x(33+1.5×2-3x)=48×2.解得x1=4,x2=8>6(不合题意,舍去).当x=4时,33+1.5×2-3x=24,24÷2=12.
答:每个生态园垂直于墙的边长为4米,平行于墙的边长为12米.
22.(8分)如图,有一段19 m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用36 m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为160 m2的长方形场地?
(2)长方形场地的面积能达到170 m2吗?如果能,请给出设计方案;如果不能,请说明理由.
解: (1)设CD=x(m),则DE=(36-2x)m.由题意,得x(36-2x)=160.整理,得x2-18x+80=0,解得x1=10,x2=8.当x1=10时,36-2x=16<19,符合题意;当x2=8时,36-2x=20>19,不合题意,舍去.∴CD=FE=10 m,DE=16 m.
(2)不能.理由如下:设CD=y(m),则DE=(36-2y)m.由题意,得y(36-2y)=170,整理,得y2-18y+85=0.∵Δ=(-18)2-4×1×85=-16<0,∴方程没有实数根,
∴长方形场地的面积不能达到170 m2.
23.(8分)某商店以20元/千克的价格购进一批商品,经调查发现,在一段时间内,销售量y(kg)与销售单价x(元)之间为一次函数关系,如图所示.
(1)求一次函数的表达式.
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
解: (1)设y关于x的函数表达式为y=kx+b,把点(20,60),(80,0)的坐标代入,得
解得∴y关于x的函数表达式为y=-x+80(20<x≤80).
(2)由题意,得(x-20)(-x+80)=800,解得x1=40,x2=60.答:销售单价应定为每千克40元或60元.
24.(8分)如图,在△ABC中,AB=6 cm,BC=4 cm,∠B=60°,动点P,Q分别从点A,B同时出发,分别沿AB,BC方向匀速移动,点P,Q的速度分别为2 cm/s和1 cm/s.当点P到达点B时,P,Q两点同时停止运动.设点P的运动时间为t(s),当t=或时,△PBQ是直角三角形.
解:由题意,得∴0
25.(8分)如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q为顶点的三角形是等腰三角形?
解:过点P作PM⊥BC于点M,则四边形PMCD为长方形,∴PM=CD=12,CM=PD=2t,CQ=t,∴QM=t,BQ=16-t,BM=16-2t.易得PD=2t≤21,∴t≤10.5.
①当PQ=BQ时,在Rt△PMQ中,PQ2=PM2+QM2=122+t2,由PQ2=BQ2,得122+t2=(16-t)2,解得t=. ②当BP=BQ时,在Rt△PMB中,BP2=BM2+PM2=(16-2t)2+122,
由BP2=BQ2,得(16-2t)2+122=(16-t)2,即3t2-32t+144=0.∵b2-4ac=-704<0,
∴3t2-32t+144=0无实数根,∴BP≠BQ.③当BP=PQ时,∵PM⊥BQ,∴BM=QM,
∴16-2t=t,解得t=.综上所述,当t=或 时,以B,P,Q为顶点的三角形是等腰三角形.
26.(10分)如图,在长方形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿边AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空:BQ= 2t cm,PB=(5-t)cm(用含 t的代数式表示).
(2)当t为何值时,PQ的长度等于5 cm
解:由题意,得(5-t)2+(2t)2=52,解得t1=0,t2=2.故当t=0或2时,PQ的长度等于5 cm.
(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.
解:存在,当t=1时,能够使得五边形APQCD的面积等于26 cm2.理由如下:
长方形ABCD的面积是5×6=30(cm2),则△PBQ的面积为30-26=4(cm2).
依题意,得(5-t)×2t×=4,解得t1=4,t2=1.当t=4时,2t=8>6,故t=4不符合题意,舍去.故当t=1时,五边形APQCD的面积等于26 cm2.
27.(12分)如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm.
(1)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.若点P,Q分别从点A,B同时出发,则经过几秒后,△PBQ的面积等于8 cm2
(2)点P从点A开始,沿AB边向点B以1 cm/s的速度移动,点Q从点B开始,沿BC边向点C以2 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能,请说明理由.
(3)若点P从点A出发,沿射线AB方向以1 cm/s的速度移动,点Q从点C出发,沿射线CB方向以2 cm/s的速度移动,点P,Q同时出发.问:经过几秒后,△PBQ的面积为1 cm2
【解】 (1)设经过x(s)后,△PBQ的面积等于8 cm2,由题意,得(6-x)·2x=8,解得x1=2,x2=4.经检验,x1,x2均符合题意,故经过2 s或4 s后,△PBQ的面积等于8 cm2.(2)不能.理由如下:设经过y(s),线段PQ将△ABC分成面积相等的两部分,由题意,得S△ABC=×6×8=24(cm2),∴(6-y)·2y=12,∴y2-6y+12=0.∵Δ=b2-4ac=36-4×12=-12<0,∴此方程无实数根,∴线段PQ不能将△ABC分成面积相等的两部分.
(3)由题意得,在6 s内,点P在线段AB上,超过6 s,点P在线段AB的延长线上;
在4 s内,点Q在线段CB上,超过4 s,点Q在线段CB的延长线上.
分三种情况讨论:①当点P在线段AB上,点Q在线段CB上,即运动时间不超过4 s时,
设经过m(s)后,△PBQ的面积为1 cm2,由题意,得(6-m)(8-2m)=1,解得m1=5+(不合题意,舍去),m2=5-.②当点P在线段AB上,点Q在射线CB上,即运动时间超过4 s,不超过6 s时,设经过n(s)后,△PBQ的面积为1 cm2,由题意,得(6-n)(2n-8)=1,
解得n1=n2=5.③当点P在射线AB上,点Q在射线CB上,即运动时间超过6 s时,
设经过k(s)后,△PBQ的面积为1 cm2,由题意,得(k-6)(2k-8)=1,解得k1=5+,k2=5-(不合题意,舍去).综上所述,经过(5-)s或5 s或(5+)s后,△PBQ的面积为1 cm2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
